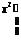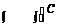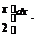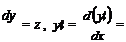ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР

1. Егер (1') дифференциалдық тең деудің оң жағ ы тек х-тен

тə уелді функция болса, яғ ни:

y = f (x),

онда тең деуді біртіндеп интегралдау арқ ылы шешеді.

y = (y)^¢ = болғ андық тан, тең деуді

d (y) = f (x) dx.

тү рінде жазамыз.

Тең деуді мү шелеп интегралдап,

y = f (x) dx + C ₁

аламыз, мұ ндағ ы C ₁ - еркін тұ рақ ты.

Енді y = екенін ескеріп,

dy = (_∫ f (x) dx + C ₁) dx

тең деуін аламыз.

Тең деуді мү шелеп интегралдап, тең деудің жалпы шешімін аламыз:

y = (_∫ f (x) dx + C ₁) dx + C ₂ = (_∫ f (x) dx) dx + C ₁ x + C ₂ ,

мұ ндағ ы, C ₂ - еркін тұ рақ ты.

Мысал. Мына дифференциалдық тең деуді шешейік:

y = x.

¢

Шешуі.у² = болғ андық тан, бастапқ ы тең деу

= x ⇒ d (y) = xdx

тең деуімен мə ндес. Тең деуді мү шелеп интегралдап,

у¢ = + C ₁

аламыз.

Енді

x ² _

 

тең деуін аламыз. Тең деуді мү шелеп интегралдап, берілген екінші

ретті дифференциалдық тең деудің жалпы шешімін аламыз

y =+ C ₁ x + C ₂,

мұ ндағ ы C ₁ мен С₂ - еркін тұ рақ тылар.

2. Егер дифференциалды тең деу жазылуында у ( х) функция

кірмесе, яғ ни:

F (x, y, y) = 0,

онда тең деуді шешу ү шін:

y = z

деген айнымалы енгізіліп, реті тө мендетіледі. Мұ ндағ ы z

айнымалы x -тен тə уелді функция деп қ арастырамыз, z = z (x).

Сонда, y = z, y = (y) = z = екендігін кө реміз. Осы мə ндерді

тең деуге қ ойсақ, бірінші ретті дифференциалдық тең деу аламыз:

F (x, z, z) = 0.

Тең деуді шешіп, z -ті табамыз, z (x) = j (x, C ₁). Табылғ ан

функцияны y = z тең деуге қ оямыз

y = j (x, C ₁).

Тағ ы бір рет интегралдап екінші ретті дифференциалдық тең деу

шешімін табамыз:

y = C ₁) dx + C ₂ .

Мысал. x (y + 1) + y = 0 дифференциалдық тең деуді

шешейік.

¢ ¢ ¢ ¢

бірінші ретті дифференциалды тең деуге келеді:

x (z + 1) + z = 0.

х-ке бө ліп,

1

z + z = -1

x

сызық ты тең деу аламыз, мұ нда, P (x) =, Q (x) = -1. Тең деудің

шешімін табу ү шін екінші дə рістегі (3) формуланы қ олданамыз:

x x e ^{-ln x} [ C - e ^{ln xdx} ]= x ^-1[ C - ∫

 

C x

=

x 2

Сызық тытең деушешімі: -

y = z болғ андық тан,

C x

dy = - 

 ^{x 2}

Мү шелеп интегралдаймыз:

dy = -

 ^x

Соң ында берілген екінші ретті дифференциалдық тең деу шешімін

табамыз:

x ²

y = C × ln x - + C ₁

3. Егер дифференциалды тең деу жазылуында х тə уелсіз

айнымалы кірмесе, яғ ни:

F (y, y, y) = 0,

онда тең деуді шешу ү шін у-ті тə уелсіз айнымалы деп,

y = z

деген айнымалы енгізіліп, реті тө мендетіледі. Мұ ндағ ы, z

айнымалы y -тен тə уелді функция деп қ арастырамыз, z = z (y).

	Сонда, y =

dz dy

× = z × z

dy dx

екендігін кө реміз. Осы мə ндерді тең деуге қ ойсақ, бірінші ретті

дифференциалдық тең деу аламыз:

F (y, z, z × z) = 0.

Тең деуді шешіп, z -ті табамыз, z (x) = j (y, C ₁). Табылғ ан

функцияны y = z тең деуге қ оямыз:

y = j (y, C ₁).

Айнымалысын ажыратып, = dx, мү шелеп интегралдап,

j (y, C ₁)

екінші ретті дифференциалдық тең деу шешімін табамыз:

= x + C ₂,

мұ ндағ ы, C ₁ мен С₂ - еркін тұ рақ тылар.

Мысал. 2 yy = (y) + 1 дифференциалдық тең деуді

шешейік.

Шешуі. z = z (y) = y деп алсақ, онда:

y = × = z z,

жə не берілген тең деу

2 yzz = z + 1.

тү ріне келеді. Бұ л айнымалысы ажыратылатын тең деу:

2 zdz

z +1

Интегралдасақ,

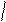
ln(z + 1) = ln y + ln C ₁,

dy

= dx, осыдан:

C ₁ y - 1

C ₁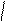

C ₁ y - 1 = (x + C ₂ )

немесе екінші ретті дифференциалдық тең деу шешімін табамыз:

y = (x + C ₂ ) +.