Бірінші ретті БІРТЕКТІ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУ

Бірінші ретті дифференциалдық тең деуді қ арастырайық

y = f (x, y).

Біртекті дифференциалдық тең деу біртекті функция

ұ ғ ымымен байланысты.

Егер кез келген a ү шін осы тең деудің оң жағ ындағ ы

f (x, y) функцияғ а қ атысты

f (ax, ay) = a f (x, y) (9)

қ атынасы орындалса, онда f (x, y) функциясын х жə не у

айнымалылары бойынша k реттібіртектіфункция деп атайды.

1-мысал. f (x, y) = x ² - xy функцияны біртектілікке

зерттейік.

Шешуі. (9) қ атынасты берілген функция ү шін жазайық:

f (ax, ay) = (ax) - ax × ay = a (x ² - xy) = a f (x, y

k=2 болғ андық тан f (x, y) = x ² - xy функцияекі ретті біртекті

функция болады екен.

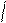
бірінші ретті біртекті

функция екенін кө рсету керек.

Шешуі. (9) қ атынасты берілген функция ү шін жазайық:

f (ax, ay) = (ax) + (ay) = a x ² + y ² = af (x, y) _.

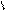
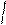
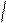
k=1 болғ андық тан f (x, y) =

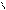
біртекті функция болады.

3-мысал. f (x, y) = - нө лінші ретті біртекті

функция екенін кө рсету керек.

Шешуі. (9) қ атынасты берілген функция ү шін жазайық:

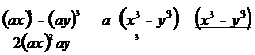3

f (ax, ay) = = = = a f (x, y)

2 a x ² y 2 x ² y

k=0 болғ андық тан берілген функция бірінші ретті біртекті

функция болады.

функциясын x жə не y аргументтердің

қ атынасының функциясы ретінде жазуғ а болады

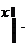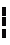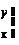немесе f (x, y) = g 

Erep f (x, y) функциясы x жə не y бойынша нө лінші ретті

біртекті функция болса, онда y = f (x, y) бірінші ретті

дифференциалдық тең деу біртекті тең деуге келтіріледі.

Егер y = f (x, y) тең деу

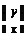y' = g

тү рінде жазылатын болса, ол бiртектi дифференциалдық тең деу

деп аталады.

Бұ л тең деуді шешу ү шін:

z =

деген жаң а айнымалы енгіземіз. Осыдан

дифференциалдап, y = z + x × z, (5) тең деуге

екенін ескеріп, тең деуді

x × dz = (g (z) - z) dx

тү рінде кө шіріп жазсақ, айнымалысы ажыратылатын тең деу

аламыз. Тең деудің екі жағ ын x × (g (z) - z) кө бейткішке бө ліп

айнымалысын ажыратамыз,

dz dx

g (z) - z x

Ал айнымалысы ажыратылғ ан тең деуді шешу белгілі.

Мысалы, (x - y) ydx - x ² dy = 0 тең деуді шешу керек.

екенін ескеріп тең деуді:

(x - y) y

y =

x ²

11

Сонда: f (ax, ay) = = = a f (x, y).

f (x, y) = - нө лінші ретті біртекті функция болғ андық тан

x

тең деу біртекті тү рге келеді:

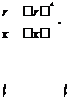y =- 

Шешу ү шін z = деген жаң а айнымалы енгізіп, осыдан

y = x × z y = z + x × z, тең деуге қ оямыз:

z + x × z = z - z.

екенін ескеріп, тең деуді

x × dz = - z

тү рінде кө шіріп жазсақ, айнымалысы ажыратылатын тең деу

аламыз. Тең деудің екі жағ ын x × z кө бейткішке бө ліп

айнымалысын ажыратамыз, = -.

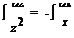Мү шелеп интегралдаймыз,

1 1 x

z z C

Енді z = белгілеуді орнына қ ойсақ,

x x

y C

екендігі шығ ады. Шешім болып тұ рғ ан функция айқ ын емес тү рде

алынды. Кейде оны дифференциалдық тең деудің жалпы

интегралы деп те атайды.

Мысал. Кə сіпорынның t мезеттегі ө ндірген ө нім кө лемі

y = y (t) болсын. Ең бек ө німділігі ө ндірген ө нім кө леміне тең

болатын кө лемді есептеу керек.

Шешуі. Ең бек ө німділігі y (t) ө нім кө лемінің туындысы

болады. Олай болса, есеп шарты мынадай

y (t) = y (t).

Осы дифференциалдық тең деуді шешейік:

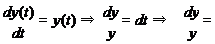∫ ∫ ^{dt ⇒ ln y = t + ln C .}

Осыдан тең деудің жалпы шешімі y = Ce^t, мұ ндағ ы С еркін

тұ рақ ты. Егер t = 0 болса, y (0) = C болады, демек есептің

мазмұ нына байланысты С бастапқ ы ө нім кө лемі. 1 сағ аттан кейінгі

кө лем y (1) = Ce ¹ . Осы екі шаманың қ атынасын алсақ

y (1) Ce

, бір сағ атта жұ мыс кө лемі 2, 7 есеге артатынын

y (0) C

кө реміз.