Cұрақ . Бірінші ретті ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР

Табиғ аттағ ы қ ұ былыстар, қ оғ амдағ ы қ атынастар, дербес

жағ дайда, экономикалық шамалар да уақ ытқ а немесе бір-біріне

қ атысты ө згеріп отырады. Ə р қ ұ былыстың ө зіне тə н ө згеру

жылдамдығ ы, ө згеріс заң дылығ ы бар. Қ ұ былыс y = f (x)

қ атынасымен берілсе, ө згеріс жылдамдығ ы оның туындысымен

сипатталады. Ал қ ұ былыс пен оның ө згеру жылдамдығ ының

байланысы дифференциалдық тең деулер арқ ылы сипатталады.

Анық тама. Дифференциалдық тең деу депхтə уелсіз

айнымалы, одантə уелді y = f (x) функцияжə неоның тү рліретті

туындыларынө зарабайланыстыратынтең деудіайтамыз:

F (x, y, y,..., y ⁽ⁿ⁾ ) = 0. (1)

Дифференциалдық тең деу ретi деп тең деудегі

туындының жоғ ары ретін айтамыз.

Мысалы, y - y = 0, xy + y = 0, x (y)² + y = e ^{- x} – бірінші

ретті дифференциалдық тең деулер; y + xy + y = e ^{- x} – екінші

ретті дифференциалдық тең деу; y = 5 x ⁴ + 7 – ү шінші ретті

дифференциалдық тең деу.

Дифференциалдық тең деу шешімі деп оны тепе-тең дікке

айналдыратын y = y (x) функцияны айтамыз. Дифференциалдық

тең деудің шешімі болатын функцияның графигі интегралдық

қ исық деп аталады.

Дифференциалдық тең деу шешімінде саны тең деу ретіндей

болатын C_i (i -тең деу реті) еркін тұ рақ тылар болса,

y = f (x, C ₁, C ₂,..., C_n ),

шешімнен еркін тұ рақ тылардың нақ тылы бір мə ніндегі алынғ ан

шешім дербес шешім деп аталады.

Мысалы, xy + y = 0 тең деудің жалпы шешімі y =

болады, мұ ндағ ы C қ андай да бір тұ рақ ты сан. Шынында да, осы

функция тең деуді тепе-тең дікке айналдырады,

 ^x  

Дифференциалдық тең деудің шешімі болатын интегралдық

қ исық тар 1- суретте кескінделген.

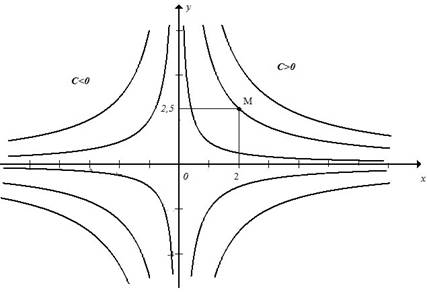
Сурет

Дифференциалдық тең деудің берілген бастапқ ы шартты

қ анағ аттандыратын дербес шешімін табуды Коши есебі дейді.

Коши есебінде бастапқ ы шарт:

y (x ₀ ) = y ₀ , y (x ₀) = y ₁ , y (x ₀) = y ₂,...

тү рінде беріледі жə не оның саны дифференциалдық тең деу ретімен

бірдей болады.

Қ арастырғ ан мысалдағ ы дифференциалдық тең деуге

бастапқ ы шарт қ ойсақ, Коши есебін аламыз:

xy + y = 0, y (2) = 2, 5.

Дифференциалдық тең деудің жалпы шешімі y =. Осы шешімдегі

x пен у орнына бастапқ ы шарттарды қ оямыз, 2, 5 = да, еркін

тұ рақ тыны табамыз, C = 5 мə нді табамыз. Табылғ ан мə нді жалпы

шешімге қ ойып, y = дифференциалдық тең деудің берілген

бастапқ ы шартты қ анағ аттандыратын дербес шешімін немесе

Коши есебінің шешімін табамыз.

Графиктік тү рде дербес шешімді табу дегеніміз жалпы

интегралдық қ исық тардың арасынан M (2; 2, 5) нү ктені басып

ө тетін қ исық ты табу деген сө з (1- сурет).

Дифференциалдық тең деулер қ алай пайда болатындығ ына

мысалдар қ арастырайық.

1. Бастапқ ы температурасы q ₀ дене температурасы 0⁰

(q ₀. Уақ ытқ а (t) байланысты дене

температурасының ө згеріс заң дылығ ын анық тау керек.

Шешуі. Дененің t мезеттегі температурасы q (t) болсын.

Осы температура D t уақ ытта D q = q (t + D t) - q (t) шамағ а

ө згереді. Орта температурасы дене температурасынан тө мен

lim = - q болады. Физикадан дене температурасының ө згеріс

D t ®0

4

жылдамдығ ы дененің сол мезеттегі температурасына

пропорционал екендігі белгілі, яғ ни:

q = - k × q, 2)

мұ ндағ ы, k > 0 пропорционалдық коэффициенті.

(2) тең деу уақ ытқ а байланысты дене температурасының

ө згеріс заң дылығ ын береді. Бұ л тең деу t тə уелсіз айнымалы, одан

тə уелді q (t) функциясы жə не оның q (t) туындысын

байланыстырып тұ рғ ан дифференциалдық тең деу. Тең деудің

жалпы шешімі

q = Ce ^{- kt} ,

мұ ндағ ы, С еркін тұ рақ ты (Шешім қ алай табылғ андығ ы кейінірек

айтылады). Есепте t = 0 уақ ыт мезетіндегі температура q ₀. Осы

шартты жалпы шешімге қ ойып,, еркін тұ рақ тының

C = q ₀ екенін кө реміз. Осы табылғ ан мə нін жалпы шешімдегі

орнына апарып қ ойсақ, (2) дифференциалдық тең деудің дербес

шешімін аламыз:

q = q ₀ e ^{- kt}.

2. Статистикалық мə ліметтердің қ орытындысы бойынша

қ андай да бір уақ ыт аралығ ындағ ы ө мірге келген балалар мен

ө мірден ө ткен адамдар саны сол мезеттегі халық тың санына тура

пропорционал екен. Халық санының ө згеру заң дылығ ын сипаттау

керек.

Шешуі. t мезеттегі халық саны y = y (t) болсын. D t

уақ ытта ө мірге k ₁ y D t бала дү ниеге келеді де, k ₂ y D t адам

дү ниеден ө теді, мұ ндағ ы, k ₁ мен k ₂ сə йкес пропорционалдық

коэффициенттер. Сонда D t уақ ытта халық тың D y ө сімі ө мірге

келген балалар мен ө мірден ө ткен адамдар санының айырымына

тең, яғ ни:

D y = k ₁ y D t - k ₂ y D t.

k ₁ - k ₂ = k деп белгілеп, ө рнекті ық шамдасақ,

= ky.

D t ® 0 жағ дайда шекке кө шсек,

y = ky

дифференциалдық тең деу аламыз. (3) тең деу уақ ытқ а байланысты

халық санының ө згеру заң дылығ ын сипаттайды. Бұ л тең деу t

тə уелсіз айнымалы, одан тə уелді y (t) функциясы жə не оның y (t)

туындысын байланыстырып тұ рғ ан дифференциалдық тең деу.

Тең деудің жалпы шешімі:

y = Ce^kt ,

мұ ндағ ы, С еркін тұ рақ ты. Егер t = 0 болса, y = C болады,

демек, есептің мазмұ нына байланысты С бастапқ ы халық саны

екен.

3. Кə сіпорынның t мезеттегі ө ндірген ө нім кө лемі

y = y (t) болсын. Осы тауарды р бағ амен сатады десек,

кə сіпорынның осы мезеттегі табысы Y (t) = p × y (t) болады.

Кə сіпорынды кең ейтуге жұ мсалғ ан инвестицияны I (t) деп

белгілейік жə не ол табыстің бір бө лігін қ ұ райды

I (t) = m × Y (t) = m × p × y (t),

m пропорционалдық коэффициенті, 0 < m < 1.

Ө нім ө ндіру жылдамдығ ы y (t) инвестицияғ а про-

порционал болады, яғ ни:

y (t) = l × I (t)

(4) жə не (5) қ атынастардан:

дифференциалдық тең деу аламыз. Мұ ндағ ы, k = mpl.

Енді дифференциалдық тең деу шешімін табу мə селесіне

кө шейік. Дифференциалдық тең деудің шешімін табу ү дерісін

тең деуді интегралдау дейді.

9 Сұ рақ