
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коды БХЧ
|
|
Коды Боуза-Чоудхури-Хоквенгема (Bose-Chadhuri-Hocquenghem — ВСН, БХЧ) являются результатом обобщения кодов Хэмминга, которое позволяет исправлять множественные ошибки. Они составляют мощный класс циклических кодов, который обеспечивает достаточную свободу выбора длины блока, степени кодирования, размеров алфавита и возможностей коррекции ошибок. В табл. 6.4 приводятся наиболее часто употребляемые при создании кодов БХЧ генераторы g(x) [8] с разными значениями п, к и t для блоков длиной до 255. Коэффициенты g{x) представлены восьмеричными числами, оформленными так, что при преобразовании их в двоичные символы крайние правые разряды отвечают коэффициенту нулевой степени в g(x). С помощью табл. 6.4 можно легко проверить свойство циклического кода — полиномиальный генератор имеет порядок п - к. Коды БХЧ очень важны, поскольку при блоках, длина которых равна порядка несколько сотен, коды БХЧ превосходят своими качествами все другие блочные коды с той же длиной блока и степенью кодирования. В наиболее часто применяемых кодах БХЧ используется двоичный алфавит и блок кодового слова длиной  , где т = 3, 4,....
, где т = 3, 4,....
Из названия табл. 6.4 Л2 ясно, что показаны генераторы только для примитивных кодов БХЧ. Термин " примитивные" (primitive) — это теоретико-числовое понятие, требующее алгебраического рассмотрения [7, 10-11], которое представлено в разделе 8.1.4Л2. На рис. 6.21 и 6.22 изображены графики вероятности ошибки для двух кодов БХЧ: (127, 64) и (127, 36). На рис. 6.21 показана зависимость 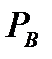 от вероятности ошибки в канальном символе при жестком декодировании. На рис. 6.22 показана зависимость
от вероятности ошибки в канальном символе при жестком декодировании. На рис. 6.22 показана зависимость 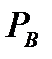 от
от 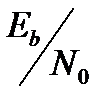 для когерентно де модулирован но го сигнала BPSK в гауссовом канале. Кривые на рис. 6.22 выглядят совсем не так, как можно было бы ожидать. Все они имеют одну и ту же длину блока, но большая избыточность кода (127, 36) не дает той эффективности кодирования, какая имеется у менее избыточного кода (127, 64). Известно, что относительно широкий максимум эффективности кодирования, в зависимости от степени кодирования при фиксированном n, для кодов БХЧ находится примерно между степенью 1/3 и 3/4 [12]. Стоит также отметить, что передача по гауссову каналу сильно ухудшается при переходе от очень высоких до очень низких степеней [11].
для когерентно де модулирован но го сигнала BPSK в гауссовом канале. Кривые на рис. 6.22 выглядят совсем не так, как можно было бы ожидать. Все они имеют одну и ту же длину блока, но большая избыточность кода (127, 36) не дает той эффективности кодирования, какая имеется у менее избыточного кода (127, 64). Известно, что относительно широкий максимум эффективности кодирования, в зависимости от степени кодирования при фиксированном n, для кодов БХЧ находится примерно между степенью 1/3 и 3/4 [12]. Стоит также отметить, что передача по гауссову каналу сильно ухудшается при переходе от очень высоких до очень низких степеней [11].
На рис. 11.23 показаны расчетные характеристики кодов БХЧ для когерентно демо-дулированного сигнала BPSK с жестким и мягким декодированием. Мягкое декодирование для блочных кодов не применяется из-за своей сложности, хотя оно и дает увеличение эффективности кодирования порядка 2 дБ по сравнению с жестким декодированием. При данной степени кодирования вероятность ошибки при декодировании уменьшается с ростом длины блока п [4]. Таким образом, при данной степени кодирования интересно рассмотреть необходимую длину блока для сравнения характеристик жесткого и мягкого декодирования. На рис. 6.23 все коды показаны со степенью кодирования, равной приблизительно 1/2. Из рисунка [13] видно, что при фиксированной степени кодирования и жестком декодировании кода БХЧ длиной 8л или более наблюдаются лучшие характеристики, чем при мягком декодировании кода БХЧ длиной п. Существует специальный подкласс кодов БХЧ (которые были разработаны раньше кодов БХЧ), который является недвоичным набором; это коды Рида-Соломона (Reed-Solomon code). Подробнее об этих кодах будет рассказано в разделе 8.1.
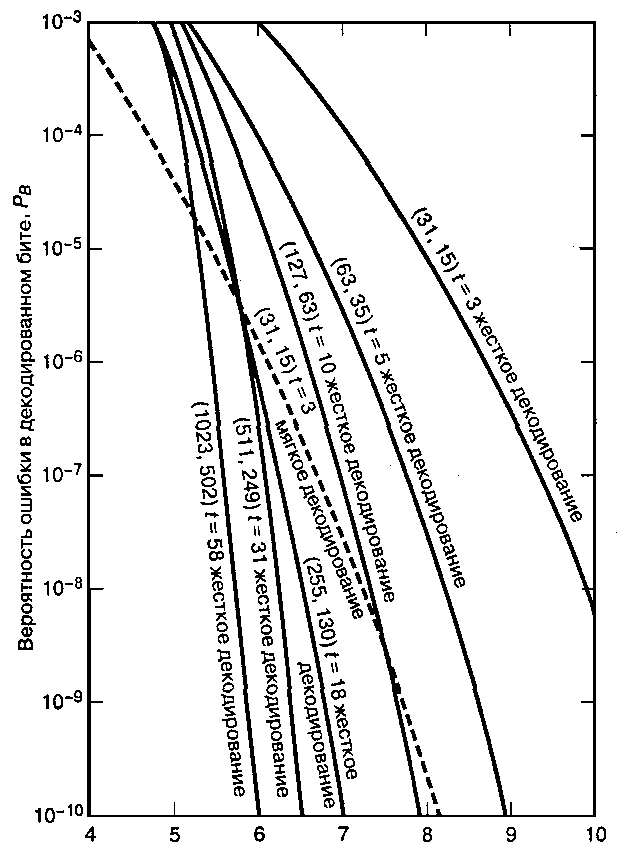
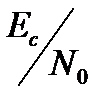 (дБ)
(дБ)
Рис. 11.23. Зависимость 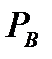 от
от 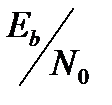 для когерентно де-модулируемого сигнала BPSK в гауссовом канале с использованием кодов БХЧ. (Перепечатано с разрешения автора из L. J. Weng. " Soft and Hard Decoding Performance Comparison for BCH Codes", Proc. Int. Conf. Commun., 1979, Fig. 3, p. 25.5.5.
для когерентно де-модулируемого сигнала BPSK в гауссовом канале с использованием кодов БХЧ. (Перепечатано с разрешения автора из L. J. Weng. " Soft and Hard Decoding Performance Comparison for BCH Codes", Proc. Int. Conf. Commun., 1979, Fig. 3, p. 25.5.5.
Основная литература 4[155: 174].
Дополнительная литература 13[78: 96].
Контрольные вопросы
1.Какие методы от ошибок вам известны?
2.Что такое код Голея?
3.Чем отличается от других кодов БХЧ?
Лекция №14. (2 час.)
|
|