Спектральная плотность энергии

Общая энергия действительного, энергетического сигнала х(t), определенного в интер­вале (− ∞, ∞), описывается уравнением (1.7). Используя теорему Парсеваля [1], мы мо­жем связать энергию такого сигнала, выраженную во временной области, с энергией, выраженной в частотной области:

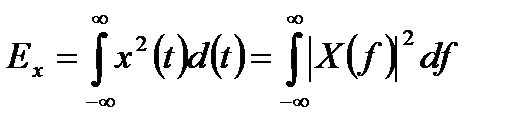, (3.5)

где Х(f) — Фурье-образ непериодического сигнала х(t). (Краткие сведения об анализе Фурье можно найти в приложении А.) Обозначим через ψ _x(f) прямоугольный ампли­тудный спектр, определенный как

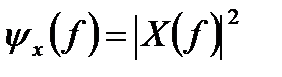. (3.6)

Величина ψ _x(f) является спектральной плотностью энергии (ESD) сигнала х(t). Следова­тельно, из уравнения (1.13) можно выразить общую энергию х(t) путем интегрирова­ния спектральной плотности по частоте:

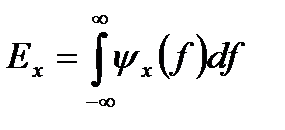. (3.7)

Данное уравнение показывает, что энергия сигнала равна площади под ψ _x(f) на графике в частотной области. Спектральная плотность энергии описывает энергию сигнала на единицу ширины полосы и измеряется в Дж/Гц. Положительные и отрицательные частотные компоненты дают равные энергетические вклады, поэтому, для реального сигна­ла x(t), величина | X(f) | представляет собой четную функцию частоты. 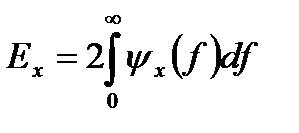. (3.8) Следовательно, спектральная плотность энергии симметрична по частоте относительно начала координат, а общую энергию сигнала x(t) можно выразить следующим образом:

Основная литература 2 [42-43];.

Дополнительная литература 3 [4-5], 5 [11-15, 69-71].

Контрольные вопросы:

1.Что такое детерминированные сигналы?

2.дайте определение энергетическим и мощностным сигналом?

3.Из чего состоит спетральная плотность сигнала?

Лекция №4 (2 час.)