
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Каноническое уравнение эллипса
|
|
Определение 4. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек 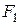 и
и 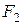 этой плоскости, называемых фокусами, есть величина постоянная (И, П, стр. 144).
этой плоскости, называемых фокусами, есть величина постоянная (И, П, стр. 144).
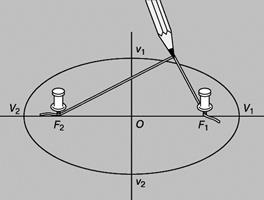
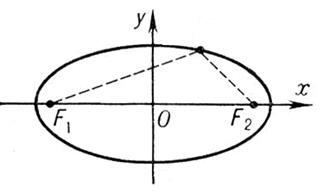
Рисунок 1- Построение эллипса Рисунок 2 – Каноническая система координат
Практическое правило построения эллипса представлено на рисунке 1 (https://dic.academic.ru/dic.nsf/enc_colier/6312/КОНИЧЕСКИЕ) практическое правило построения данного геометрического множества. Нетрудно понять, что если фокусы совпадают, то эллипс превращается в  окружность.
окружность.
Определение 5. Середина отрезка 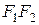 , соединяющего фокусы, называется центром эллипса. (А, стр. 72).
, соединяющего фокусы, называется центром эллипса. (А, стр. 72).
Определение 6. Вся прямая 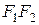 , называется его фокальной или первой осью. (А, стр. 72).
, называется его фокальной или первой осью. (А, стр. 72).
Определение 7. Прямая, проходящая через центр эллипса перпендикулярно к фокальной оси, называется второй осью эллипса. (А, стр. 72).
Определение 8. Расстояние между фокусами 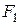 и
и 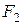 называется фокусным расстоянием (А, стр. 72).
называется фокусным расстоянием (А, стр. 72).
Для вывода канонического уравнения эллипса декартову прямоугольную систему координат Оху выбирают следующим образом: начало координат О размещают в центре эллипса, т.е. на середине отрезка 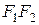 , в качестве оси Ох выбирают фокальнуюось (рисунок 2). Если фокусы
, в качестве оси Ох выбирают фокальнуюось (рисунок 2). Если фокусы 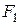 и
и 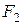 совпадают, то за ось Ох можно взять любую ось, проходящую через точку О. Система координат такого вида называется канонической системой (для данного эллипса) (А, стр. 73).
совпадают, то за ось Ох можно взять любую ось, проходящую через точку О. Система координат такого вида называется канонической системой (для данного эллипса) (А, стр. 73).
Пусть длина отрезка 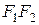 равна
равна 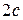 ,
, 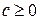 (случай
(случай 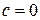 , соответствует совпадению фокусов), тогда, в выбранной системе координат, координаты точек
, соответствует совпадению фокусов), тогда, в выбранной системе координат, координаты точек 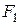 и
и 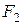 -
- 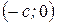 и
и 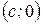 , соответственно (рисунок 3). Фокус
, соответственно (рисунок 3). Фокус 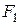 в этом случае условно называют левым фокусом, а фокус
в этом случае условно называют левым фокусом, а фокус 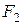 - правым фокусом (А, стр. 73)
- правым фокусом (А, стр. 73)
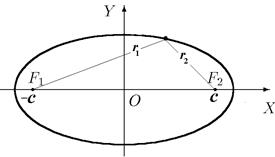

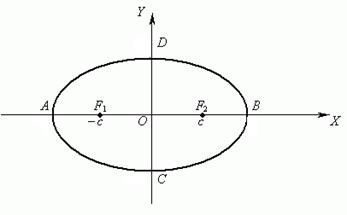
Рисунок 3 – Координаты фокусов Рисунок 4 – Отрезки расстояний
Пустьсумма расстояний от точек эллипса (исследуемого геометрического множества точек) до фокусов 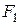 и
и 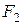 равно
равно 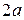 , очевидно, что
, очевидно, что 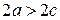 (это следует из свойств треугольников), случай
(это следует из свойств треугольников), случай 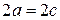 приводит к ситуации, когда точка располагается на отрезке
приводит к ситуации, когда точка располагается на отрезке 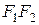 и эллипс вырождается в отрезок. Следовательно,
и эллипс вырождается в отрезок. Следовательно, 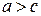 . Пусть
. Пусть 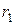 - расстояние от точек эллипса до фокуса
- расстояние от точек эллипса до фокуса 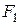 ,
,  - расстояние до фокуса
- расстояние до фокуса 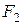 (рисунок 4).
(рисунок 4).
Пусть 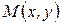 - произвольная точка плоскости. Точка M принадлежит данному эллипсу (данному геометрическому месту точек L) тогда и только тогда, когда
- произвольная точка плоскости. Точка M принадлежит данному эллипсу (данному геометрическому месту точек L) тогда и только тогда, когда
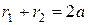 . (4)
. (4)
Так как
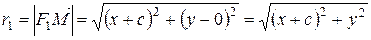 , (5)
, (5)
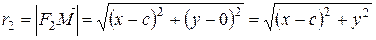 ; (6)
; (6)
то, подставляя (5) и (6) в уравнение (4), получаем, уравнение (7):
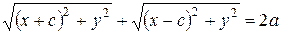 . (7)
. (7)
Перенося втрое слагаемое левой части уравнения в правую часть, получаем уравнение (8):
 , (8)
, (8)
возводя в квадрат обе части уравнения (8), и проводя несложные преобразования, получаем уравнение (9)
 ,
,
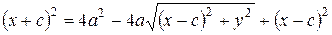 ,
,
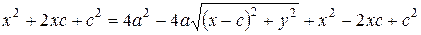 ,
,
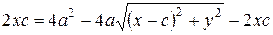 ,
,
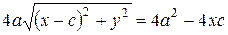 ,
,
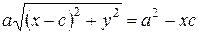 . (9)
. (9)
Снова возводя в квадрат обе части уравнения (9), и проводя необходимые преобразования, получаем уравнением (10):
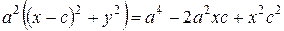 ,
,
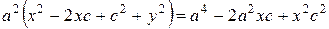 ,
,
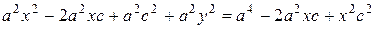 ,
,
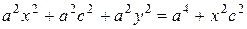 ,
,
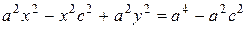 ,
,
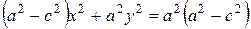 . (10)
. (10)
Как мы уже отметили ранее, 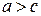 , поэтому
, поэтому 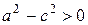 и, следовательно, можно ввести обозначение (11):
и, следовательно, можно ввести обозначение (11):
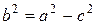 , (11)
, (11)
уравнение (10) можно представить в виде (12):
 . (12)
. (12)
Разделив обе части уравнения (12) на 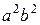 , получаем уравнение (13)
, получаем уравнение (13)
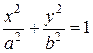 . (13)
. (13)
Так как уравнение (13) является следствием уравнения (7), то координаты любой точки эллипса будут удовлетворять уравнению (13). Однако в процессе вывода мы использовали метод последовательного возведения в квадрат, следовательно, могли появиться «лишние корни» (И., П., стр. 145; А, стр. 73-74). Поэтому необходимо показать, что любая точка 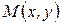 , координаты которой удовлетворяют уравнению (13) принадлежит рассматриваемому эллипсу, т.е. выполняется равенство (4).
, координаты которой удовлетворяют уравнению (13) принадлежит рассматриваемому эллипсу, т.е. выполняется равенство (4).
Пусть координаты точки 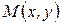 удовлетворяют уравнению (13). Тогда
удовлетворяют уравнению (13). Тогда
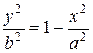 ;
; 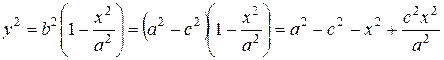 .
.
Опираясь на формулы (5) и (6), получаем, что в этом случае:
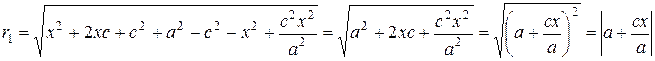
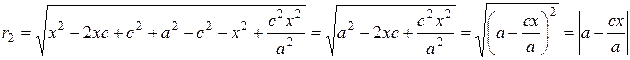 .
.
 Из уравнения (13) следует, что
Из уравнения (13) следует, что 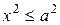 , следовательно,
, следовательно, 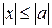 . По постановке задачи:
. По постановке задачи: 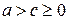 , следовательно,
, следовательно, 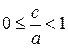 . Это означает, что
. Это означает, что
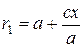 ,
, 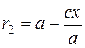 , (14)
, (14)
и 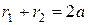 .
.
Определение 9. Уравнение (13) называется каноническим уравнением эллипса (И.П., стр. 14, А, стр. 73).
Определение 10. Число 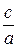 называется эксцентриситетом эллипса (А, стр. 72).
называется эксцентриситетом эллипса (А, стр. 72).
В литературе встречаются следующие обозначения для эксцентриситета: 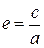 (А, стр. 72) или
(А, стр. 72) или 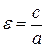 (Г, стр. 47). Выберем второй вариант обозначения:
(Г, стр. 47). Выберем второй вариант обозначения:
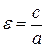 . (15)
. (15)
Как уже было отмечено выше
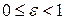 . (16)
. (16)
Эксцентриситет равен нулю только в том случае, когда фокусы совпадают. Опираясь на полученные выше результаты, нетрудно получить (А, стр. 74), что
 ; (17)
; (17)
 (18)
(18)
Используя уравнение (13) легко увидеть, что эллипс обладает следующими свойствами (А, стр. 74 – 75):
1) обе оси эллипса являются его осями симметрии;
2) центр эллипса является его центром симметрии;
3) весь эллипс лежит в прямоугольнике, ограниченном прямыми 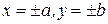 , который называется основным прямоугольником для данного эллипса (рисунок 5, https://topreferat.znate.ru/docs/index-21429.html);
, который называется основным прямоугольником для данного эллипса (рисунок 5, https://topreferat.znate.ru/docs/index-21429.html);
4) пересекается с осями координат в точках 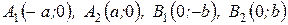 , которые называются вершинами эллипса (рисунок 5).
, которые называются вершинами эллипса (рисунок 5).
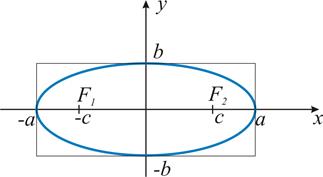
Рисунок 5 – Основной прямоугольник
Определение 11. Отрезки 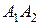 и
и 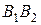 , соединяющие противоположные вершины эллипса, а также их длины
, соединяющие противоположные вершины эллипса, а также их длины 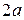 и
и 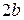 , называются большой и малой осями эллипса (П, стр. 77). Величины a и b называются соответственно большой и малой полуосями эллипса соответственно (И, П., стр. 146).
, называются большой и малой осями эллипса (П, стр. 77). Величины a и b называются соответственно большой и малой полуосями эллипса соответственно (И, П., стр. 146).
Название определяется тем, что 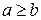 . Нетрудно заметить, что при
. Нетрудно заметить, что при  , уравнение (13) задает окружность с центром в начале координат радиуса
, уравнение (13) задает окружность с центром в начале координат радиуса 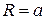 .
.
|
|