Доказательство. Проще всего доказать данную теорему методом от противного

Проще всего доказать данную теорему методом от противного. Предположим, что векторы линейно зависимы. Тогда найдется нетривиальный набор коэффициентов 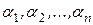, при котором линейная комбинация векторов обратится в нуль, т.е. .

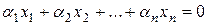Умножая обе части данного равенства скалярно на вектор 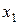, получим:

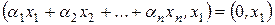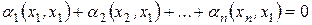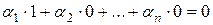, из свойств скалярного произведения следует, что . Так как система векторов является ортонормированной, то и .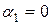

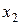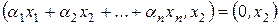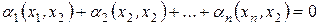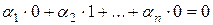Умножая обе части указанного выше равенства скалярно на вектор , получим: , из свойств скалярного произведения следует, что . Так как система векторов является ортонормированной, то и .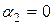

Выполняя эту же операцию далее с векторами 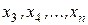получим, что 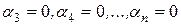. Таким образом, линейная комбинация векторов обращается в нуль только при тривиальном наборе коэффициентов, что противоречит, высказанному предположению. Следовательно, система векторов является линейно независимой. Утверждение доказано.

Теорема 5. В конечномерном евклидовом пространстве можно выбрать ортонормированный базис.

Доказательство. Рассмотрим алгоритм построения ортонормированного базиса при n =3.

Пусть задано некоторое евклидово пространство 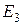. Так как исследуемое евклидово пространство является линейным пространством размерности 3, то любая система из трех линейно независимых векторов образует базис. Зафиксируем любые три из них и обозначим 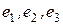соответственно. Так как пространство является евклидовым, то в нем определено скалярное произведение.

Ортонормированный базис будем строить, опираясь на выбранные векторы 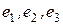и правило определения скалярного произведения векторов, по следующей схеме. Сначала построим ортогональную систему векторов .

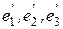Выберем 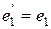, а 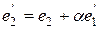, подбирая коэффициент 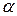так, чтобы .

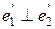Вектор 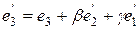, подбирая коэффициенты 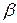и 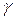так, чтобы вектор 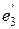был ортогонален векторам 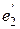и .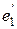

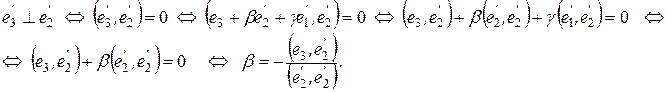
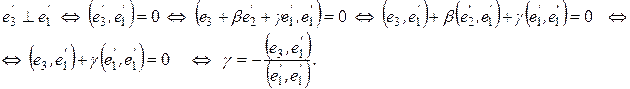
Полученную ортогональную систему превращаем в ортонормированную следующим образом:

.

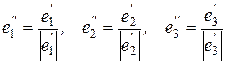Ортонормированный базис построен.