Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Геометрическое изображение суммы и разности комплексных чисел.
|
|
Геометрическая интерпретация комплексных чисел позволяетнаглядно истолковать сумму и разность двух комплексных чисел. Пусть даны два комплексных числа z 1= a 1+ b 1 i и z 2= a 2+ b 2 i. Их суммой будет комплексное число z 1+ z 2=(a 1+ a 2)+(b 1+ b 2) i. С другой стороны, известно, что при сложении векторов их соответственные координаты складываются.
рис. 1
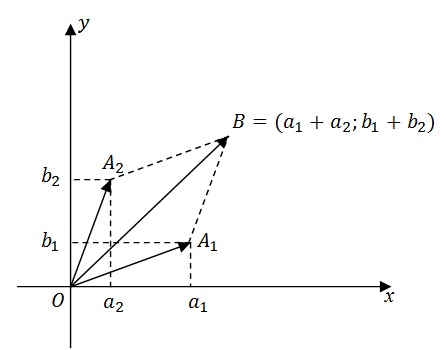
рис. 2
Поэтому, если вектор OA 1 имеет координаты (a 1; b 1) (рис. 1), а вектор OA 2 - координаты (a 2; b 2), то их сумма (вектор OB) будет иметь координаты (a 1+ a 2; b 1+ b 2). Вектор OB и есть геометрическое изображение суммы комплексных чисел z 1 и z 2.
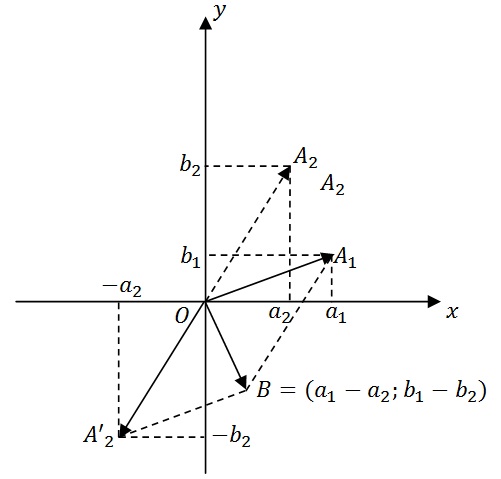
Так как разность двух комплексных чисел z 1= a 1+ b 1 i и z 2= a 2+ b 2 i есть сумма комплексного числа z 1 и числа, противоположного комплексному числу z 2, то геометрически ее можно изобразить как сумму вектора OA 1 с координатами (a 1; b 1) и вектора OA 2 с координатами (− a 2; − b 2) (рис. 3), т. е. как вектор OB с координатами (a 1− a 2; b 1− b 2).
Текст задания:
1. Данные комплексные числа изобразить точками плоскости:
а) 1 + i; в) —2 + 3 i; д) 5+ 0 i; ж) 0 + 5 i
б) 1 — i; г) —3 — 2 i; е) —6 + 0 i; з) 0 — 4 i.
2. Какие комплексные числа изображают на рисунке 330 точки А, В, C, D и О?
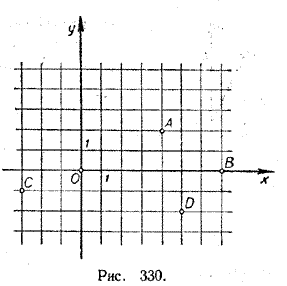
3. Дать геометрическую интерпретацию формулам:
а) (1 +2 i) + (l — 2 i)=2 + 0 i;
б) (3 — 4 i)+(— 1 + 2 i) = 2—2 i.
4. Пусть точка М служит изображением на плоскости комплексного числа а + bi.
Построить на той же плоскости точки, которые изображали бы комплексные числа:
a) а — bi; д) 0 + bi
б) — а + bi; е) — а + 0 i;
в) — а — bi ж) 0 — bi.
г) а + 0 i;
5. Пусть точка М служит изображением на плоскости комплексного числа а — bi. Где на той же плоскости расположены точки, изображающие числа:
а) 3 а + 0 i; г) 0 + 2 bi
б) — 5 а + 0 i; д) 4 а + 3 bi.
в) 0 — bi;
Раздел 2. Корни, степени, логарифмы. Функции, их свойства и графики.
Уравнения и неравенства
Самостоятельная работа № 3
Тема: Преобразование иррациональных выражений.
Цель: закрепить знания и умения студентов по освоению применения формул при выполнении вычислений и решении иррациональных уравнений.
Теоритическое обоснование:
Корень n-й степени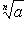 
- арифметический корень n -й степени из числа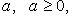 
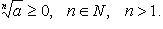
Свойства:
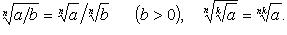
В частности,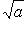 
- арифметический квадратный корень: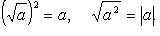 
Степень с дробным (рациональным) показателем
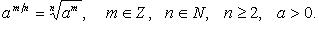
Пример 1
.
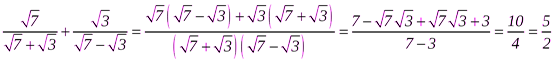Пример 2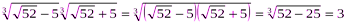 
.
Пример 3 Освободиться от иррациональности в знаменателе дроби:
.
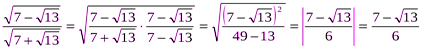Текст задания:
Упростить иррациональные выражения:
3. 
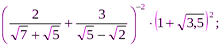
4. 
;
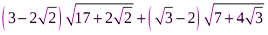5. 
;
-
.
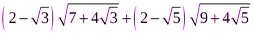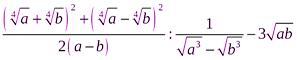Самостоятельная работа № 4
Тема: Степени с действительным показателем, действия со степенями.
Цель: закрепить знания и умения студентов по освоению свойств показательной функции.
Теоритическое обоснование:
Свойства степени с действительным показателем
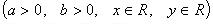
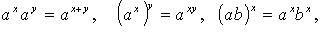
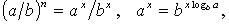
Пример 1. Вычислить: 
.
Решение.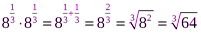 
; 
;
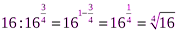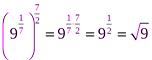. Отсюда: 
.
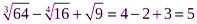Пример 2. Выполнить действия: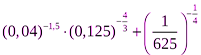 
.
Решение.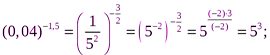 
; 
.
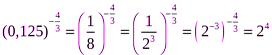Отсюда: 53∙ 24+5=(5∙ 2)3∙ 2+5=2000+5=2005.
Пример 3.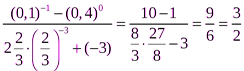 
.
Текст задания:
1. Расположить в порядке возрастания следующие числа:
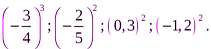
2. Вычислить: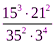 
.
3. Упростить: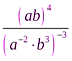 
.
4. Найти значение выражения: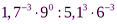 
.
5. Вычислить: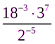 
;
6. Вычислить:
а) 3, 20 + 641/6 – 0, 23 ·0, 2-2 – 53: 5;
б) 271/3 – 4, 80 – 1, 53 –1, 5-2 + 22: 2-3;
в) 52: 5-1 +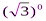 
- 42 · 4-3 – 272/3.
Самостоятельная работа № 5
Тема: Правило перехода логарифма к новому основанию.
Цель: закрепить знания и умения студентов по освоению логарифмов и свойств логарифмической функции.
Теоритическое обоснование:
|
|