Моделирование турбулентных течений. 3

6. Модели турбулентности семейства k-w.

Впервые k-w модель турбулентности была предложена Колмогоровым в 1942 г. В качестве второго параметра в этой модели Колмогоров предложил использовать скорость диссипации, приходящуюся на единицу кинетической энергии турбулентности, w. Этот параметр имеет размерность 1/с и называется средней частотой диссипации.

В дальнейшем модель k-w была развита в работах Саффмена, Сполдинга, Вилкокса и др.

Стандартная k-w модель это полуэмпирическая модель, основанная на уравнениях переноса кинетической энергии турбулентности, k, и удельной скорости диссипации, w.

Как отмечалось выше, Колмогоров (1942) предложил первую двухпараметрическую дифференциальную модель турбулентности, выбрав в качестве первого пара-

метра турбулентности кинетическую энергию турбулентных пульсаций. Вторым параметром была диссипация на единицу турбулентной энергии ω. В k - ω -модели

ω удовлетворяет дифференциальному уравнению, подобному уравнению для k. Не зная о работе Колмогорова, Саффмен (1970) сформулировал k - ω -модель, которая представляется предпочтительной по отношению к колмогоровской модели.

Сполдинг (1972) предложил улучшенную версию модели Колмогорова, в которой ему

удалось убрать некоторые из их недостатков. В дальнейшем Вилкокс, Саффмен,

Рубезин и др.(1972-1988) развили и апробировали k - ω -модели. Коклей (1983)

предложил k^1/2 - ω -модель для расчета турбулентных сжимаемых течений. В последнее десятилетие Спезайл, Ментер и др. (1990-1997) изобрели несколько моделей турбулентности рассматриваемого типа. Робинсон, Харрис и Хасан (1995) развили k - ω ²- модель.

В своей формулировке Колмогоров относился к параметру ω как к скорости диссипации энергии в единице объема и времени. Чтобы подчеркнуть его физическое

соотношение с внешним масштабом турбулентности l, он также называл его некоторой средней частотой, определяемой с помощью ω = ck^1/2/l, где c - постоянная. С другой стороны, ω является временным масштабом, на котором имеет место

диссипация турбулентной энергии. Хотя реальный процесс диссипации происходит в

мельчайших вихрях, скорость диссипации является скоростью переноса кинетической энергии турбулентности к мельчайшим вихрям. Следовательно, она определяется свойствами крупных вихрей и, таким образом, масштабами k и l, из-за чего ω косвенно ассоциируется с диссипативными процессами. Следует отметить, что по аналогии с молекулярной турбулентная вязкость пропорциональна произведению турбулентных масштабов скорости и длины, которое согласуется с колмогоровским аргументом ω»k^1/2/l. Конечно, при этом надо иметь в виду, что указанная аналогия не вполне правомочна, а аргумент Колмогорова скорее является примером из анализа размерностей, нежели выводом фундаментальной физики.

Хотя изложение модели Колмогорова было кратким, а константы замыкания установлены не полностью, по мнению Вилкокса [ 5 ], крайне удивительно, как этот великий исследователь турбулентности вывел модельные уравнения. При этом он не привел ссылок на какие-либо точные уравнения, которые бы символизировали,

каким путем он замкнул уравнение для k или других моментов. Однако легко пред-

ставить себе мотивы, основанные на анализе размерностей:

- исходным моментом является пропорциональность n_t и k;

- размерность n_t - [длина]²/[время], а k-[длина]²/[время]²;

- следовательно, n_t /k имеет размерность [время];

- диссипация турбулентности ε имеет размерность [длина]²/[время]³;

- следовательно, размерность ε /k - 1/[время];

- можно замкнуть выражения для турбулентной вязкости и уравнение для ε,

вводя переменную с размерностью [время] или 1/[время].

Следующим шагом является постулирование уравнения для ω. Во внимание

приняты только некоторые из наблюдаемых физических процессов: нестационарность, конвекция (иногда трактуемая как адвекция), диффузия, диссипация, дисперсия и генерация. Комбинируя физические соображения с анализом размерностей,

Колмогоров постулировал следующее уравнение для ω:

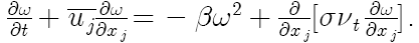
Здесь, по выражению Вилкокса, допущены некоторые вольности с обозначениями, а

k и û являются двумя новыми константами замыкания. Данное уравнение имеет

четыре примечательные черты. 1. Отсутствует генеративный член, аналогичный та-

кому же члену в уравнении для k. Это согласуется с мнением Колмогорова о том,

что ω ассоциируется с мельчайшими масштабами турбулентности и напрямую не

взаимодействует с осредненным движением. Его логика основывалась на предположении, согласно которому крупномасштабные энергоемкие вихри преимуществен-

но ответственны за определение соответствующего временного масштаба турбулентности и самой скорости диссипации. 2. Запись уравнения в терминах ω выглядит предпочтительнее, чем в терминах ω 2. Как показано Вилкоксом, решение Колмогорова записать уравнение именно для ω было воистину пророческим выбором.

3. В уравнении нет члена с молекулярной диффузией, так что оно оказывается приемлемым лишь для высокорейнольдсовых течений и не может проинтегрировано

сквозь вязкий подслой. 4. Уравнение полностью эмпирическое, обусловленное физическими соображениями.

Еще несколько замечаний по трактовке ω. Саффмен (1970) определил этот параметр как частотную характеристику самопроизвольного процесса турбулентного

распада. Он установил, что «грубой» идеей является то, что w² - осредненный

квадрат завихренности энергосодержащих вихрей, а k - кинетическая энергия движения, индуцированного этой завихренностью. Сполдинг (1972), Вилкокс и Албер

(1972), Робинсон, Харрис и Хасан (1995) идентифицировали ω как флуктуирующую

завихренность, так что ω 2 является дважды энстрофией. Вилкокс и Рубезин (1980),

Вилкокс (1988) и Спезайл и др.(1990) просто определили ω как отношение ε к k.

Уравнение для ω видоизменялось по мере совершенствования k- ω -модели на

протяжении последних 50 лет. Генеративный член был добавлен в модель всеми ее

разработчиками. Подобно Колмогорову, Вилкокс (1988), Спезайл и др.(1990), Пенг и

др.(1997) записали уравнение для ω в терминах ω в то время как в большинстве

моделей этого типа уравнения записаны относительно ω ². Следующая версия k-

ω -модели свободна от недостатка аналогичной модели Вилкокса (1988), выявлен-

ного при прогнозировании характеристик свободных сдвиговых течений. Новая модель Вилкокса (1998) формулируется как

Кинематическая вихревая вязкость: n_t = k/ω.

Турбулентная кинетическая энергия:

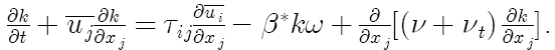
Удельная скорость диссипации:

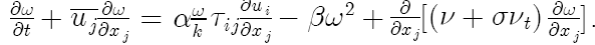
Коэффициенты замыкания и вспомогательные соотношения:

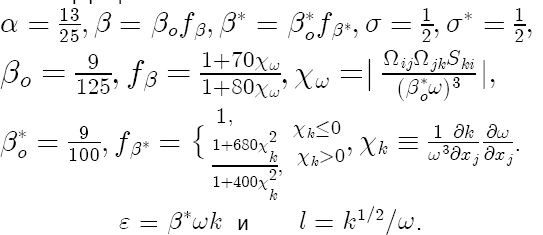
Составляющие тензоров Ω ij и Sij, появляющиеся в соотношении (6.21), являются

составляющими осредненных тензоров вращения и скоростей деформации и опре-

деляются так:

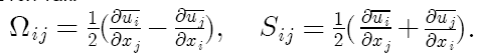
Как легко можно проверить, величина c_ω равняется нулю для двумерных течений.

Зависимость b от c_ω , взятая из работы Поупа (1978), имеет существенное влияние

для круглых и радиальных струй.

С одной стороны, новые диссипативные коэффициенты имеют очень малое

влияние в пограничных слоях, поскольку величина ω вблизи стенки довольно вели-

ка, так что c_k и c_ω малы. Это очень важно, так как старая модель Вилкокса (1988)

хорошо прогнозировала именно характеристики пограничных слоев. Новая модель в

этом отношении практически идентична старой. С другой стороны, _k и c_ω значи-

тельно больше для свободных сдвиговых течений. Следовательно, новая модель

более диссипативна в сдвиговых слоях по сравнению со старой. Это существенно по

той причине, что старая версия приводила к ускоренному расширению сдвиговых

слоев по отношению к данным измерений. Новая модель свободна от этого недостатка. Функции f _b и f _b*, как и величины a и b_o, калиброваны, чтобы прогнозируемые характеристики для дальних следов, слоев смешения, круговых и радиальных струй были согласованы с измеренными. Таким образом, предложенная Вилкоксом (1998) модель представляется более точной для расчета сложных типов течений, поскольку она точнее отображает их составные, характерные элементы (пограничные слои, следы, струи).

Отметим, что дефект старой модели Вилкокса фактически устраняется включением в правую часть уравнения для ω так называемого перекрестного диффузионного члена c_ω .