Методы взвешенных невязок

Изучив один метод относительно подробно, переходим к изложению прочих методов целыми классами. Самым распространенным классом являются методы взвешенных невязок. Они исходят из предположения, что искомую функцию можно представить в виде функционального ряда, например такого:

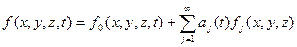
Функцию f₀ обычно стараются выбирать так, чтобы она максимально точно (по возможности) удовлетворяла начальным и граничным условиям. Аппроксимирующие (пробные) функции f_j предполагаются известными. Математики напридумывали некоторое количество требований к таким функциям, но их здесь обсуждать не будем. Ограничимся фактом, что полиномы и тригонометрические функции этим требованиям удовлетворяют. Еще несколько примеров наборов подобных функций будут рассмотрены при описании конкретных методов.

Коэффициенты a_j заранее неизвестны, и их следует определять из системы уравнений, получаемой из исходного уравнения. От бесконечного ряда берут лишь некоторое конечное число членов.

В уравнении, которое предполагается решить, все члены переписываются в левую часть, в правой части остается лишь нуль. Таким образом, уравнение приводится к виду

Если приближенное решение (записанное в виде конечной суммы заранее выбранных функций) подставить в это уравнение, то оно не будет тождественно удовлетворяться. Следовательно, можно записать

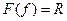
где величина R называется невязкой. В общем случае невязка является функцией x, y, z и t. Задача сводится к нахождению таких коэффициентов a_j, чтобы невязка оставалась малой во всей расчетной области. Под понятием «малой» в данных методах понимают, что интегралы по расчетной области от невязки, умноженной на некоторые весовые функции, равны нулю. То есть

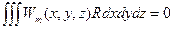
Задав конечное число весовых функций, получаем систему уравнений для нахождения неизвестных коэффициентов. Задавая различные пробные аппроксимирующие (пробные) и различные весовые функции, легко получаем целый класс методов, называемый методами взвешенных невязок.

Приведем несколько примеров простейших методов из этого класса.

Метод подобластей. Расчетная область разделяется на несколько подобластей D_m, могущих перекрывать друг друга. Весовую функцию задают в виде

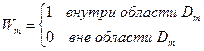
Таким образом, обеспечивается точное решение исходного уравнения почти всюду. На границах между подобластями исходное уравнение может не удовлетворяться. Метод послужил основой для ряда методов (пара из них будет рассмотрена ниже).

Метод коллокаций. В качестве весовых функций используются дельта-функция Дирака

где x= (x, y, z). Напоминаю, что функция Дирака – это хитрая функция[18], равная нулю везде, кроме начала координат. Но в начале она принимает неизвестное науке значение такое, что любой интеграл по области, содержащей начало координат, равен единице. Говоря проще: задаем некоторое количество точек (часто в данном подходе называемых узлами). Исходное уравнение будет удовлетворяться в этих точках. Существуют подходы к выбору этих точек и пробных функций, позволяющие максимизировать точность при ограниченном числе узлов. Но здесь их обсуждать не будем.

Метод наименьших квадратов. Метод основан на минимизации величины

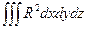
Но нетрудно показать, что он тоже принадлежит к классу методов взвешенных невязок. Весовыми функциями для него являются функции вида

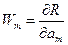
Пожалуй, это самый известный среди неспециалистов метод из данного класса, но далеко не самый популярный у специалистов.

Метод Галеркина. В этом методе в качестве весовых функций берутся аппроксимирующие (пробные) функции. То есть

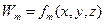
Метод широко используется в случаях, когда хотят найти решение в виде непрерывной (а не сеточной) функции.

Рассмотрим применение последних трех методов к приближенному решению задачи о распределении потенциала в плазме. В задаче рассчитывается распределение потенциала между двумя параллельными стенками с расстоянием между ними 2L. Расположим начало координат в центре между стенками и принять потенциал в центре за ноль. Как известно

предположим, что правую часть этого уравнения удалось каким-то образом записать в виде полинома от потенциала[19]. Ограничившись первыми двумя членами разложения, получаем уравнение

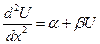
с граничными условиями U(0)=0 и

Попробуем поискать решение в виде

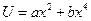
невязка при этом запишется в виде

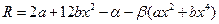
Сначала воспользуемся методом коллокаций. Узлы расположим в точках

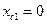
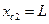
получаем уравнения

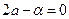
отсюда получаем

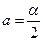
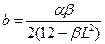
Рассмотрим метод наименьших квадратов. Имеем

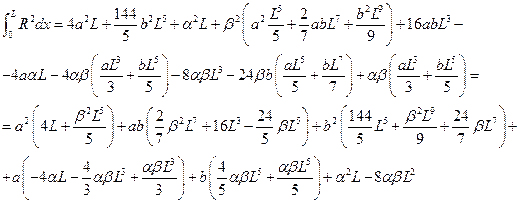
откуда получаем

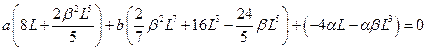
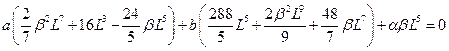
решая эту систему линейных уравнений, получаем ответ (лень писать эти длинные выражения).

Теперь посмотрим на метод Галеркина. Получаем

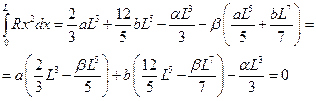
получили опять систему линейных уравнений. Опять поленюсь выписывать конечный результат.