
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 3
|
|
Применение МАИ для сравнительного анализа различных технических систем. Например, необходимо осуществить оценку четырех современных систем аккумулирования энергии на основе шести критериев. Соответствующая иерархия имеет следующий вид:
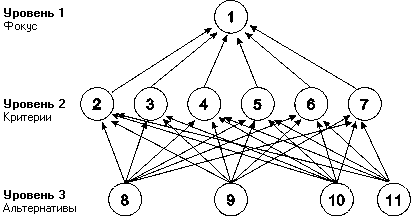
Рис. 19. Иерархия сравнительного анализа технических систем
В таблице представлены результаты парных сравнений относительно соответствующих критериев.
В качестве критериев принимались следующие:
2. Экологический.
3. Экономический.
4. Социальный.
5. Выбор места.
6. Время, требуемое для постройки.
7. Совместимость с энергосистемой.
Множество систем аккумулирования энергии включало:
8. Накопление сжатого воздуха.
9. Подземная гидроаккумуляция.
10. Электрические батареи.
11. Накопление энергии водорода.
Матрица парных сравнений к примеру 3
| Собственный вектор | |||||||
| 1/5 | 1/3 | 1/2 | 0, 09 | ||||
| 0, 42 | |||||||
| 1/2 | 1/7 | 1/5 | 1/2 | 0, 05 | |||
| 1/2 | 0, 25 | ||||||
| 1/3 | 1/2 | 0, 14 | |||||
| 1/2 | 1/7 | 1/5 | 1/3 | 0, 05 |
max= 6, 05; ИС = 0, 01; ОС = 0, 01.
После проведения этапа синтеза получено следующее ранжирование аккумулирующих систем:
-электрические батареи ‒ 0, 36;
-накопление сжатого воздуха ‒ 0, 26;
-накопление энергии водорода ‒ 0, 24;
-подземная гидроаккумуляция ‒ 0, 14.
Литература
1. Ильина Н.В. Системный анализ и моделирование процессов в техносфере: Учеб. пособие / Н.В. Ильина, Д.Д. Лапшин, В.И. Федянин. – Ч. 1. Воронеж: ГОУВПО «Воронежский государственный технический университет, 2008. – 206 с.
Лекция 15. Метод конечных элементов
15.1 Общий ход решения задачи на основе метода конечных элементов
Решение задач анализа при функциональном моделировании сводится к определению вектора V, который удовлетворяет исходным уравнениям задачи и граничным условиям. Часто искомую функцию задают в виде ряда
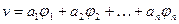 (1)
(1)
где 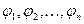 – базисные функции от независимых переменных,
– базисные функции от независимых переменных,
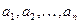 – неизвестные постоянные коэффициенты.
– неизвестные постоянные коэффициенты.
Методы определения постоянных коэффициентов весьма разнообразны. Так, в методе Ритца их находят из условия минимума потенциальной энергии системы, в методе коллокаций – из условия удовлетворения дифференциальных уравнений задачи в отдельных точках и т. д. Выбор базисных функций в конечном счете определяет успех решения задачи: если эти функции подобраны удачно, решение получается простым, в противном случае приходится удерживать большое число членов ряда (9.1), что существенно затрудняет расчет и не всегда приводит к желаемым результатам. Для простых случаев разработаны рекомендации по выбору базисных функций, в сложных случаях проблема назначения этих функций может оказаться не проще решения неходкой задачи.
Идея метода конечных элементов (МКЭ) заключается в том, что вместо поиска единого аналитического представления функции v используют ее кусочно-линейную аппроксимацию, т.е. всю область решения разбивают на подобласти конечных размеров, достаточно малых, чтобы обеспечить требуемую точность линеаризации.
Рассмотрим основы МКЭ на примере одномерной задачи, точное решение которой описывается кривой, изображенной на рис. 1, а. Прежде всего разбейте область 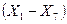 на конечные элементы
на конечные элементы 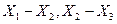 и т. д. В пределах длины каждого элемента искомую функцию можно считать линейной (рис. 1, б):
и т. д. В пределах длины каждого элемента искомую функцию можно считать линейной (рис. 1, б):
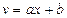 . (2)
. (2)
Если тем или иным способом вам удастся определить значения искомой функции 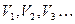 в узлах
в узлах 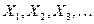 , то задача будет решенной, поскольку с учетом равенства (2) вы получите возможность вычислить приближенные значения функции в любой точке. Рассмотрим, как можно определить значения искомой функции в узлах
, то задача будет решенной, поскольку с учетом равенства (2) вы получите возможность вычислить приближенные значения функции в любой точке. Рассмотрим, как можно определить значения искомой функции в узлах 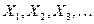 .
.
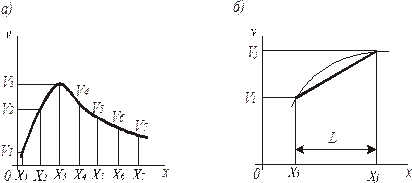
Рис. 1.Одномерные конечные элементы
Узловые значения функций вы можете искать различными способами, исходя из физического смысла задачи. Задача может быть задана в форме дифференциальных уравнений, либо в виде некоторого функционала 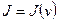 . В первом случае удобно воспользоваться методом Бубнова – Галеркина, минимизируя ошибку приближенного решения, во втором – каким-нибудь вариационным принципом, обеспечивающим минимизацию функционала. Используя кусочно-линейное представление функции и записывая функционал в виде
. В первом случае удобно воспользоваться методом Бубнова – Галеркина, минимизируя ошибку приближенного решения, во втором – каким-нибудь вариационным принципом, обеспечивающим минимизацию функционала. Используя кусочно-линейное представление функции и записывая функционал в виде 
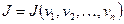 , вы обеспечите реализацию минимума энергии, приравнивая нулю частные производные:
, вы обеспечите реализацию минимума энергии, приравнивая нулю частные производные:

В результате будет получена система уравнений
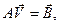
решение которой позволит вычислить вектор 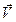 , т.е. найти значения искомой функции в узлах и тем самым решить задачу.
, т.е. найти значения искомой функции в узлах и тем самым решить задачу.
Унификация вычислительных процедур накладывает некоторые особенности на реализацию МКЭ, для уяснения которых вновь обратимся к решению одномерной задачи (рис. 1).
В общем случае алгоритм МКЭ состоит из четырех этапов:
1) выделение конечных элементов (разбиение заданной области на конечные элементы);
2) определение аппроксимирующей функции для отдельного конечного элемента (определение функции элемента);
3) объединение конечных элементов в ансамбль;
4) определение вектора узловых значений функции.
Первый этап. Первый этап расчета с использованием МКЭ состоит в разбиении области на конечные элементы. Такое разбиение начинают обычно от границы области, стараясь наиболее точно повторить ее конфигурацию, затем производят разбиение внутренних областей. Сначала выделяют достаточно крупные подобласти, которые отличаются по свойствам материала, геометрии, напряженному состоянию и пр. Затем каждую подобласть разбивают на конечные элементы принятой формы, чаще всего треугольные, при этом размеры конечных элементов могут быть приняты различными (рис. 2) в зависимости от требуемой точности описания. Резкого изменения размеров конечных элементов на границах подобластей стараются избегать.
Важное значение имеет нумерация узлов конечных элементов. Дело в том, что матрицы коэффициентов систем алгебраических уравнений в МКЭ представляют собой сильно разряженные матрицы ленточной структуры. Ненулевые элементы таких матриц располагаются параллельно главной диагонали, при этом ширина полосы зависит от числа степеней свободы узлов и их нумерации (от разности номеров соседних узлов). Выбор оптимальной нумерации узлов способствует существенному сокращению затрат вычислительных ресурсов компьютера.
Информация о разбиении области на конечные элементы и нумерации узлов является исходной для последующих этапов расчета. Обычно требуется указывать тип конечного элемента, его порядковый номер, номер узла сети, координаты этого узла, значения физических параметров в пределах конечного элемента и др. Такая топологическаяинформация обычно содержит примерно в шесть раз больше чисел, чем количество узлов сетки разбиения. Для объектов средней сложности объем такой информации измеряется сотнями тысяч. Понятно, что ручной ввод этой информации, помимо чрезвычайной утомительности, может сопровождаться ошибками.

Рис. 2. Пример разбиения подобласти на конечные элементы
Процедуры по вводу информации оптимальной нумерации узлов удается формализовать, что позволило разработать специальные программы, называемые препроцессорами, которые либо существуют в виде автономных программ, либо непосредственно включаются в состав программных комплексов, реализующих МКЭ.
В данном примере суть его понятна без пояснений: выделено шесть конечных элементов  в общем случае разных по длине.
в общем случае разных по длине.
Второй этап. Рассмотрим (рис. 1, б) один из выделенных элементов 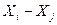 (одномерный симплекс-элемент). Для определения коэффициентов а и b полинома (2) запишем граничные условия:
(одномерный симплекс-элемент). Для определения коэффициентов а и b полинома (2) запишем граничные условия:
при 

при 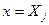

Подставляя эти значения в равенство (2), получим систему двух уравнений, решив которую относительно а и b, имеем
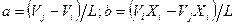 .
.
Подставляя эти коэффициенты в формулу (2), можно записать:
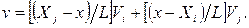 (3)
(3)
Члены уравнения (3), заключенные в скобки, называют функциями формы одномерного симплекс-элемента:
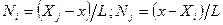 . (4)
. (4)
С учетом обозначений (4) уравнение (3) принимает вид:
 , ( 5)
, ( 5)
или в матричной форме
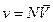 , (6)
, (6)
где  –матрица-строка,
–матрица-строка,
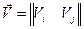 – вектор-столбец.
– вектор-столбец.
Полученные здесь формулы (4), (6) полностью характеризуют одномерный симплекс элемент. Они являются общими пригодными для решения любых задач, включающих одномерные прямолинейные конечные элементы.
Третий этап – объединение конечных элементов в ансамбль. Основу этого этапа составляет замена номеров узлов i и j в уравнении (5) на номера, присвоенные узлам в процессе разбиения рассматриваемой области. Для примера, приведенного на рис. 1, будем иметь:
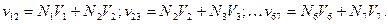
Полученная система уравнений представляет собой математическую модель исследуемой задачи. Запишем эту систему в расширенной форме:
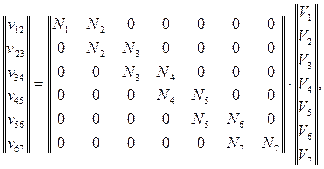 (7)
(7)
что соответствует векторной записи модели
 (7а)
(7а)
Четвертый этап – определение вектора узловых значений функции. Этот этап не является формальным, и мы не можем ограничиться ссылкой на рис. 5.1 абстрактного примера. Нужно знать конкретное дифференциальное уравнение или конкретный функционал исследуемого явления.
Допустим, что в нашем примере этот функционал имеет простейший вид:
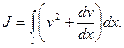 (8)
(8)
Разобьем пределы интегрирования в соответствии с делением области на конечные элементы, тогда

Первый член подынтегрального выражения определим, возведя в квадрат равенство (5), второй – путем его дифференцирования с учетом обозначений (4). Выполняя интегрирование и простейшие преобразования, можем записать:
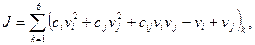 (9)
(9)
где
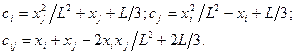
Для того, чтобы определить минимум функционала (9), приравняем нулю частные производные, предварительно развернув выражения сумм для всех шести конечных элементов и заменяя индексы i, j номерами соответствующих узлов:

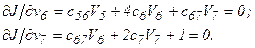
Таким образом, получена следующая система уравнений:

или
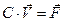 . (10)
. (10)
Матрицу С называют матрицей жесткости, а вектор 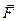 – вектором нагрузок. Эти названия пришли из строительной механики. Они отвечают сущности рассматриваемых там задач, поскольку МКЭ первоначально был разработан и в основном сформировался применительно к расчетам строительных конструкций. Затем метод конечных элементов был распространен на другие предметные области, а термины строительной механики сохранились и стали общепринятыми, хотя и отражали иную физическую сущность.
– вектором нагрузок. Эти названия пришли из строительной механики. Они отвечают сущности рассматриваемых там задач, поскольку МКЭ первоначально был разработан и в основном сформировался применительно к расчетам строительных конструкций. Затем метод конечных элементов был распространен на другие предметные области, а термины строительной механики сохранились и стали общепринятыми, хотя и отражали иную физическую сущность.
Дальнейший расчет сводится к обращению матрицы С и определению вектора 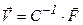 . Зная компоненты вектора
. Зная компоненты вектора 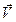 и используя систему уравнений (7), можно вычислить значение искомой функции в любой точке. Таким образом, задача полностью решена.
и используя систему уравнений (7), можно вычислить значение искомой функции в любой точке. Таким образом, задача полностью решена.
Выше было отмечено, что узловые значения функции определяются дифференциальным уравнением задачи или условием минимизации некоторого функционала. В ряде случаев эти операции не требуется выполнять в явном виде. Можно использовать какой-нибудь другой принцип, отвечающий физической сущности задачи. Так, используя уравнения метода перемещений при расчете строительных конструкций, мы автоматически минимизируем функционал энергии системы, поскольку канонические уравнения указанного метода являются следствием такой минимизации.
При рассмотрении примера (рис. 1) конечная задача состояла в определении функции 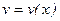 . Часто такая функция может быть лишь промежуточным звеном между координатой х и другой переменной, подлежащей определению. Так, уравнение изогнутой оси балки интересует нас не как геометрический объект конфигурации системы, а как функция, позволяющая вычислить изгибающие моменты и поперечные силы или нормальные и касательные напряжения. В таком случае соответствующие зависимости между этими величинами могут быть включены в состав конечных элементов и в их ансамбль.
. Часто такая функция может быть лишь промежуточным звеном между координатой х и другой переменной, подлежащей определению. Так, уравнение изогнутой оси балки интересует нас не как геометрический объект конфигурации системы, а как функция, позволяющая вычислить изгибающие моменты и поперечные силы или нормальные и касательные напряжения. В таком случае соответствующие зависимости между этими величинами могут быть включены в состав конечных элементов и в их ансамбль.
15.2 Сети одномерных конечных элементов
На рис. 3 приведены примеры из различных предметных областей с одинаковой топологией с точки зрения теории графов, имеющие одинаковый принцип построения математической модели на основе МКЭ.
На рис. 3, а показана электрическая схема из семи резисторов. Источники питания на схеме не показаны, но их влияние характеризуется токами 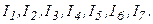
Если резистор 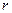 рассмотреть изолированно от системы, то с помощью закона Ома можно записать соотношение между исходящими токами
рассмотреть изолированно от системы, то с помощью закона Ома можно записать соотношение между исходящими токами 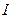 и напряжениями
и напряжениями 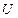 на его концах:
на его концах:
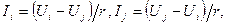 (11)
(11)
или в матричной форме
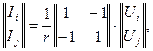 (12)
(12)
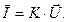 (12 а)
(12 а)
Узлы сети и ее элементы можно нумеровать произвольно, однако при выделении каждого элемента условимся под индексом i всегда понимать меньший номер. Нетрудно видеть, что  поэтому силу тока в узле i можно определять по формуле
поэтому силу тока в узле i можно определять по формуле
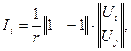 (13)
(13)
а если рассматривается узел  , то правую часть формулы (13) следует умножить на -1.
, то правую часть формулы (13) следует умножить на -1.

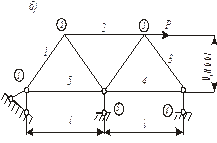
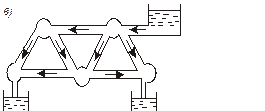
а) электрическая; б) механическая; в) гидравлическая
Рис. 3 Сети одномерных конечных элементов:
При составлении ансамбля конечных элементов запишем уравнения «равновесия» (закон Кирхгофа) поочередно для каждого узла. Для формализации процедуры будем рассматривать все элементы сети независимо от того, примыкают они к данному узлу или нет. Если элемент примыкает к рассматриваемому узлу своим началом, будем принимать равенство (13) со своим знаком, т. е. умножать его на 1. Если это окажется конец элемента, то будем вводить множитель – 1. Если элемент не примыкает к узлу, то принимать множитель 0. С целью сокращения записей условимся матрицу жесткости обозначать буквой К, снабженной индексом, указывающим номер элемента. Для первого узла (рис. 3, а) будем иметь:
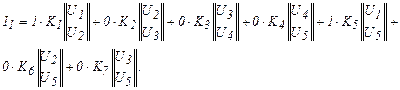
для второго узла
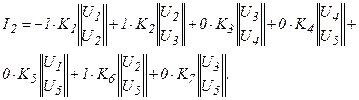
Поступая аналогично с остальными узлами, можем записать математическую модель электрической системы:
 (14)
(14)
При рассмотрении элементов анализа сетей было дано определение и указан прием построения матрицы инциденций ориентированного графа. Здесь мы получили такую матрицу, занумерованные узлы и элементы сети.
Перейдем к рассмотрению механической системы (рис. 3, 6) в виде фермы, загруженной силой Р. Предварительно отметим существенное отличие этой системы от ранее рассмотренной. В электрической системе сила тока есть скалярная величина, поэтому не имеет значения пространственное расположение резисторов, важен лишь факт их примыкания к данному узлу. Для фермы все иначе: здесь имеет значение не только топология, но и геометрия фермы, а также ориентация внешних сил и реакций связей. Для плоской фермы с шарнирными узлами каждый узел имеет две степени свободы, что определяет 10 степеней свободы для всей совокупности узлов. Однако внешние связи исключают две степени свободы в первом узле и по одной (в вертикальном направлении) – в 4 и 5 узлах. Для учета этого обстоятельства необходимо вычеркнуть соответствующие строки матрицы S, характеризующей степени свободы системы (две строки для первого узла и вторые строки – для 4 и 5 узлов):
 (15)
(15)
При рассмотрении конечного элемента для электрической системы основным параметром, определяющим связь между фазовыми переменными I и U, было электрическое сопротивление резистора r, а сама связь устанавливалась законом Ома.
В случае фермы фазовыми переменными будут усилия в стержнях N и удлинения стержней 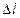 , параметром – погонная жесткость
, параметром – погонная жесткость 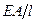 , а связь переменных состояния определится законом Гука
, а связь переменных состояния определится законом Гука 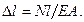
15.3 Виды конечных элементов
Выше были рассмотрены системы, включающие одномерные симплекс-элементы, при этом функции формы элемента (4) оставались одинаковыми для задач из разных предметных областей. Физическая сущность задачи отображается матрицей жесткости. В электрических системах эта матрица зависит от сопротивлении R, емкостей С, индуктивностей L элементов, составляющих систему. В системах, характеризующих работу строительных конструкций, матрица жесткости непосредственно связана с погонными жесткостями 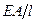 для растянутых (сжатых) элементов,
для растянутых (сжатых) элементов, 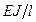 – для изгибаемых элементов и т.д. Для нелинейных систем, например, для схемы «в» (рис. 2), где связь между напором V и расходом J имеет вид
– для изгибаемых элементов и т.д. Для нелинейных систем, например, для схемы «в» (рис. 2), где связь между напором V и расходом J имеет вид 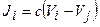 , матрица жесткости будет представлять уже не массивы констант, а некоторые функции от напора жидкости.
, матрица жесткости будет представлять уже не массивы констант, а некоторые функции от напора жидкости.
В случае функции двух переменных х, у используют плоские конечные элементы в виде многоугольников, обычно треугольника и прямоугольника.
Рассмотрим двумерный симплекс-элемент, представляющий собой плоский треугольник (рис. 4).
Интерполяционный полином, аппроксимирующий непрерывную функцию v(x, у) внутри симплекс-элемента, имеет вид
 (16)
(16)
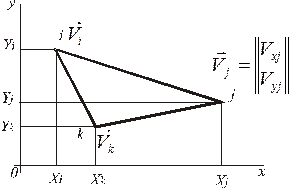
Рис. 4.Двумерный симплекс-элемент
Для придания этому выражению вида, удобного для применения в методе конечных элементов, будем поступать так же, как это делали на втором этапе п.п. 15.1 [см. формулы (1)...(6)]. Граничные условия будут иметь вид:
при 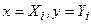 функция v (x, у) примет значение
функция v (x, у) примет значение  ;
;
при 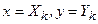 функция v(x, у) примет значение
функция v(x, у) примет значение 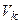 .
.
Используя формулу (16), получим систему трех уравнений для определения коэффициентов  Подставляя эти коэффициенты в полином (16) и проделав необходимые преобразования, аналогичные рассмотренным в п. 15.1, запишем аналогичную (5) формулу
Подставляя эти коэффициенты в полином (16) и проделав необходимые преобразования, аналогичные рассмотренным в п. 15.1, запишем аналогичную (5) формулу
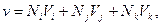 (17)
(17)
где функции формы элемента имеют вид:
 (18)
(18)
Здесь ∆ – площадь треугольника конечного элемента;
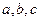 – коэффициенты, определяемые путем круговой перестановки индексов выражений:
– коэффициенты, определяемые путем круговой перестановки индексов выражений:
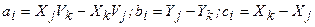 . (19)
. (19)
Формулы (16)...(19) будут одинаковыми для всех задач, где используют треугольные симплекс-элементы. Матрицы жесткостей будут зависеть от физической сущности задачи. Рассмотрим это на примере плоской задачи теории упругости. Заметим, что в этом случае каждый узел имеет две степени свободы, поэтому вектор 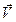 имеет две компоненты vx и
имеет две компоненты vx и 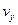 каждую из которых определяют по формуле (17).
каждую из которых определяют по формуле (17).
Деформации внутри конечного элемента можно выразить через перемещения с помощью зависимостей Коши:

Выполняя дифференцирование равенства (17) с учетом обозначений (18), запишем зависимости Коши в матричной форме:
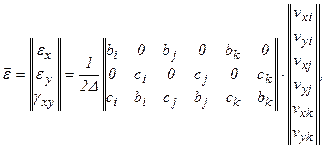 (20)
(20)
или
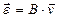 . (20 а)
. (20 а)
Для перехода от деформаций тела к напряжениям используем закон Гука при плоском напряженном состоянии:
 (21)
(21)
или
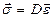 . (21 а)
. (21 а)
Матрицы D и В содержат всю информацию о конечном элементе: матрица D определяет его упругие характеристики а матрица В – геометрические. Остается определить еще одну матрицу (матрицу жесткости К), которая связывает усилия, действующие в узлах конечного элемента, с перемещениями этих узлов. Для записи этой матрицы воспользуемся принципом возможных перемещений, согласно которому при равновесии тела работа внешних сил Р на возможных перемещениях узлов 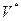 т. е.
т. е. 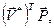 равна по величине работе внутренних сил на тех же перемещениях:
равна по величине работе внутренних сил на тех же перемещениях: 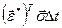 , где
, где 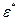 – деформация, отвечающая возможным перемещениям;
– деформация, отвечающая возможным перемещениям; 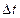 – объем конечного элемента. В результате преобразований получим искомую связь между усилиями в узлах конечного элемента и перемещениями этих узлов:
– объем конечного элемента. В результате преобразований получим искомую связь между усилиями в узлах конечного элемента и перемещениями этих узлов:
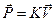 , (22)
, (22)
где матрица жесткости К будет равна
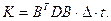
 (23)
(23)
Матрица жесткости (23) конечного элемента не зависит от действующих на элемент нагрузок и поэтому остается неизменной для всех нагружений. Элементы этой матрицы представляют собой коэффициенты канонических уравнений метода перемещений для расчета одного конечного элемента.
Рассмотрим объединение конечных элементов в ансамбль на примере простейшей сети из трех конечных элементов (рис. 5).
Для каждого конечного элемента мы можем записать формулу (17), заменяя узлы 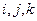 конкретными номерами. Так, для первого элемента
конкретными номерами. Так, для первого элемента
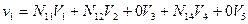 .
.
Поступая аналогично с остальными узлами, получим:
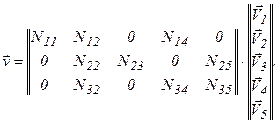 (24)
(24)
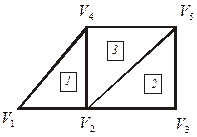
Рис.5.Ансамбль трех конечных элементов
Напомним, что узловые значения искомой функции
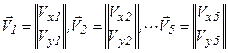
пока еще не известны и подлежат определению. С этой целью нужно использовать какой-нибудь принцип, выражающий физическую сущность задачи. В задачах строительной механики таким принципом могут быть уравнения равновесия с учетом совместности перемещений. Когда мы все это проделаем, задача будет решенной, поскольку формулы (20), (21), (24) с учетом обозначений (18), (19) позволяют определить в любой точке области нормальные и касательные напряжения, найти угловые и линейные деформации, вычислить перемещения данной точки в направлении осей х и у. Совокупность указанных формул, полностью определяющих поведение исследуемой системы, составляет ее математическую модель.
Перейдем к объединению конечных элементов в ансамбль.
Пусть в узлах системы конечных элементов действуют внешние силы, определяемые вектором
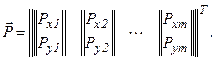 (25)
(25)
К каждому i- му узлу сети примыкает в общем случае 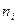 конечных элементов, каждый из которых вносит свой вклад в матрицу жесткости. Поэтому для каждого i -го узла суммарная матрица жесткости будет представлять собой сумму элементов матриц жесткости всех примыкающих к узлу элементов, т.е.
конечных элементов, каждый из которых вносит свой вклад в матрицу жесткости. Поэтому для каждого i -го узла суммарная матрица жесткости будет представлять собой сумму элементов матриц жесткости всех примыкающих к узлу элементов, т.е.
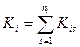 , (26)
, (26)
в то время, как узловые перемещения для всех этих элементов будут общими в силу совместности перемещений всех элементов, соединенных в i- м узле. Поскольку узлы имеют две степени свободы, вектор перемещения i -го узла будет содержать две компоненты перемещений  точно так же, как внешняя сила [см. формулу (25)] имеет две компоненты Pxi, Pyi. Совокупность перемещений всех m неопорных узлов сети конечных элементов определится m -мерным вектором перемещений:
точно так же, как внешняя сила [см. формулу (25)] имеет две компоненты Pxi, Pyi. Совокупность перемещений всех m неопорных узлов сети конечных элементов определится m -мерным вектором перемещений:
 (27)
(27)
Общую матрицу жесткости для всей конструкции можно выразить в виде
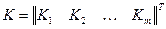 . (28)
. (28)
Окончательная зависимость между вектором сил (25) и вектором перемещений (27) будет иметь вид
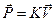 . (29)
. (29)
Таким образом, вектор узловых значений искомой функции будет равен
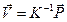 . (30)
. (30)
Литература:
1. Ильина Н.В. Системный анализ и моделирование процессов в техносфере: Учеб. пособие / Н.В. Ильина, Д.Д. Лапшин, В.И. Федянин. – Ч. 1. Воронеж: ГОУВПО «Воронежский государственный технический университет, 2008. – 206 с.
Лекция 16. Аналитические модели сложных систем
16.1 Основные понятия
Математическое моделирование позволяет устанавливать зависимости выходных (y1, у2,..., уn) переменных от входных переменных (x1, x2,..., хn) при целенаправленном изменении внутренних параметров (h1, h2,..., hn) с учетом в ряде случаев воздействия внешней среды. Наиболее просто эта задача решается, если известна функциональная зависимость между соответствующими многомерными векторами:
 (1)
(1)
В таком виде математическую модель удается получить только для очень простых ситуаций. В обычных условиях математическое описание процессов в исследуемом объекте задают в форме системы дифференциальных уравнений. Понятно, что ЭВМ не может непосредственно оперировать даже с простейшими зависимостями типа (1), поэтому построение математических моделей подразумевает комплекс преобразований этих зависимостей до уровня, допускающего численное решение, и последующую реализацию такого решения на основе программ анализа в виде элементарных арифметических и логических операций.
В простейших ситуациях исходная задача может быть представлена системой линейных алгебраических уравнений, которая легко сводится к последовательности элементарных операций (ПЭО) на основе стандартных процедур с использованием библиотечных программ. Если модель задана системой нелинейных алгебраических уравнений, то возможны либо непосредственный переход к ПЭО, либо предварительная линеаризация с дальнейшим переходом к ПЭО (рис. 1).
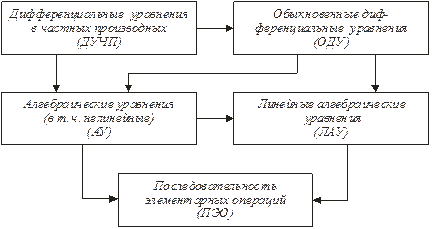
Рис. 1.Преобразования уравнений при построении аналитических моделей
Наиболее типичными являются модели, в которых исследуемый процесс описывается обыкновенными дифференциальными уравнениями или дифференциальными уравнениями в частных производных. Численные решения таких уравнений основаны на дискретизации переменных или алгебраизации задачи. Дискретизация заключается в замене непрерывных переменных конечным множеством их значений в заданных для исследования интервалах, а алгебраизация – в замене производных алгебраическими соотношениями, Если дифференциальные уравнения в частных производных описывают статическое состояние, то дискретизация и алгебраизация преобразуют дифференциальные уравнения в систему алгебраических уравнений, в общем случае нелинейных. Так, если рассматриваются переменные, изменяющиеся в пространстве и во времени, то при решении задачи на первом этапе устраняются производные по пространственным координатам, что позволяет перейти к обыкновенным дифференциальным уравнениям, а затем – производные по времени с переходом к алгебраическим уравнениям. Дальнейшее решение задачи может выполняться на основе метода простых итераций, либо быть сведено к предварительной линеаризации на основе метода Ньютона с переходом к линейным алгебраическим уравнениям. Решение системы таких уравнений выполняется с помощью прямых методов, например, метода Гаусса.
Ниже рассмотрена цепочка последовательных преобразований, которая позволяет однотипными приемами решать различные задачи. За базовое принято численное решение дифференциальных уравнений первого порядка с заданными начальными условиями (задача Коши) и системы таких уравнений. К подобным уравнениям может быть приведено обыкновенное дифференциальное уравнение n-го порядка. Дифференциальное уравнение с заданными граничными условиями может быть представлено как редукция к задаче Коши и тем самым решено аналогичными способами.
16.2 Приближенное решение ОДУ при заданных начальных условиях
Математическое моделирование систем, описываемых обыкновенным дифференциальным уравнением при заданных начальных условиях, осуществляется наиболее просто, если уравнение в явном виде разрешено относительно производной:
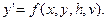
От влияния внутренних параметров h и воздействий внешней среды v можно избавиться, повторяя решение заданного уравнения при фиксированных значениях этих параметров h =const, v =const.
Рассмотрим дифференциальное уравнение первого порядка
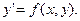 (2)
(2)
Если требуется найти интегральную кривую у = у (х), проходящую через заданную точку М0 (х0, у0), то формулируется задача Коши: найти решение у = у (х) уравнения, удовлетворяющее начальному условию у (х0)= у0.
Существуют различные приемы решений такой задачи: метод последовательных приближений, интегрирование уравнений с помощью степенных рядов, методы Адамса, Крылова, Милна и др. Ниже рассмотрены методы Эйлера и Рунге-Кутта, первый из которых является наиболее наглядным, а второй – наиболее популярным.
16.3 Метод Эйлера и его модификации
Принцип численного решения уравнения (2) при начальном условии у (х0)= у0, основанный на методе Эйлера, чрезвычайно прост. Он непосредственно вытекает из смысла производной. Подставляя заданное начальное значение х0 и у0 в правую часть Исходного уравнения (2), мы определим производную в этой точке: y' (х=х0) =f (х0, у0), т. е. найдем тангенс угла наклона касательной к искомой кривой. Это дает возможность определить приближенное значение функции в соседней точке при x1 = x0 + h (рис. 2). При этом приращение функции будет  , а полное значение ординаты при этом составит
, а полное значение ординаты при этом составит  . Таким образом, получены приближенные координаты соседней точки x1, y1, принимая которые за исходные, мы можем повторить вычисления методом Эйлера и найти следующую точку с координатами х2, у2. Аналогично вычисляются все последующие точки по формулам
. Таким образом, получены приближенные координаты соседней точки x1, y1, принимая которые за исходные, мы можем повторить вычисления методом Эйлера и найти следующую точку с координатами х2, у2. Аналогично вычисляются все последующие точки по формулам
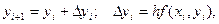 (3)
(3)
где h – достаточно малый шаг приращений координаты х.
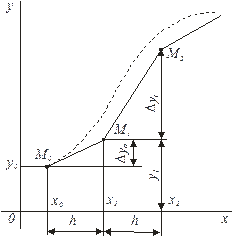
Рис. 2.К решению уравнения методом Эйлера
Для того чтобы назначить величину шага, обеспечивающую необходимую точность вычислений, расчет повторяют при шаге, в два раза меньшем первоначального. Если разница в результатах вычислений превышает требуемую точность, то шаг разбиения уменьшают еще раз и повторяют расчет.
Метод Эйлера приводит к систематическому накоплению ошибок, поэтому в практике расчетов используют модификации этого метода: метод ломаных и метод Эйлера-Коши.
В первом случае сначала вычисляют промежуточные значения
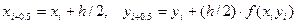
и находят направление поля интегральных кривых в средней точке
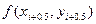 , а затем полагают
, а затем полагают 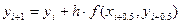 .
.
Во втором случае грубое приближение
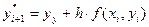 ,
, 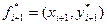 уточняется следующим образом:
уточняется следующим образом:

Дальнейшим развитием и уточнением метода Эйлера являются различные схемы метода Рунге-Кутта. Ниже рассмотрена одна из таких схем, получившая наибольшее распространение.
16.4 Метод Рунге-Кутта
Основная схема метода Рунге-Кутта имеет вид:
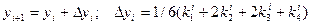 (4)
(4)
где

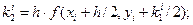
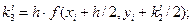 (5)
(5)

(i = 1, 2, …, n).
Для определения правильности выбора шага h выполняют двойной пересчет, как это было отмечено при рассмотрении метода Эйлера.
16.5 Приближенное решение ДУ n-го порядка при заданных начальных условиях
Для дифференциального уравнения n -го порядка
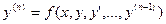 (6)
(6)
задача Коши состоит в нахождении решения
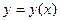
удовлетворяющего начальным условиям
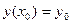 ;
; 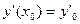 ; …;
; …; 
где x0, y0, yo’… ‒ заданные числа. Такая задача может быть приведена к решению системы дифференциальных уравнений путем подстановок
 ,
, 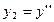 , …,
, …,  (7)
(7)
Будем иметь:

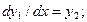 (8)
(8)
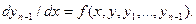
Дальнейшее решение задачи выполняют как указано выше, например, методом Рунге-Кутта.
Для примера найдем приближенное решение нелинейного дифференциального уравнения свободных колебаний маятника в среде, обладающей сопротивлением. Пусть  – угол отклонения маятника от положения равновесия, t – время. Полагая, что сопротивление среды пропорционально угловой скорости маятника, имеем для
– угол отклонения маятника от положения равновесия, t – время. Полагая, что сопротивление среды пропорционально угловой скорости маятника, имеем для  =
=  (t) нелинейное дифференциальное уравнение второго порядка
(t) нелинейное дифференциальное уравнение второго порядка
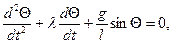 (9)
(9)
где 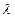 – коэффициент затухания колебаний;
– коэффициент затухания колебаний;
g – ускорение свободного падения;
l – длина маятника.
Принимая 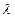 =0, 2, g / l = 10, приходим к уравнению
=0, 2, g / l = 10, приходим к уравнению
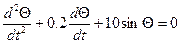 (10)
(10)
с начальными условиями: угол отклонения 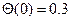 , угловая скорость
, угловая скорость  .
.
Выполняя подстановки типа (9), т.е. полагая 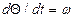 , запишем уравнение (10) в виде системы уравнений
, запишем уравнение (10) в виде системы уравнений
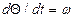 ,
,
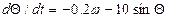 (11)
(11)
Приближенное решение этой системы будем искать методом Рунге-Кутта, используя зависимости (9). При этом роли  и
и 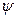 в уравнениях (9) будут исполнять их значения:
в уравнениях (9) будут исполнять их значения:
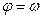 ,
,
 .
.
Примем: h =0, 1; 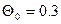 ,
, 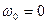 . При i =0 находим:
. При i =0 находим:
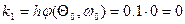 ;
;
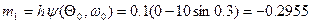 ;
;
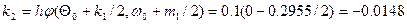 ;
;
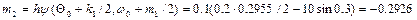 ;
;
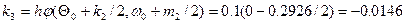 ;
;
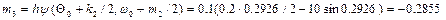
 ;
;
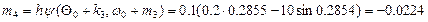 ;
;
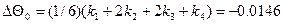 ;
;
 .
.
Следовательно, при t1 =0, 1, имеем:
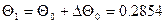 ;
; 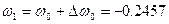
Продолжая процесс вычислений для других значений ti, последовательно можем определить все интересующие нас значения 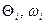 .
.
16.6 Приближенное решение ДУ при заданных граничных условиях (краевых задач)
Рассмотренные выше приемы решений обыкновенных дифференциальных уравнений при заданных начальных условиях в одной точке получены путем последовательного интегрирования уравнения по участкам, на которые может быть разбит весь интервал задания подынтегральной функции. В краевой задаче, когда для дифференциального уравнения заданы граничные условия в различных точках, необходимо получить решение в виде общего интеграла. Для решения таких более сложных задач существуют различные способы. Мы рассмотрим лишь некоторые из них, позволяющие свести решения краевых задач к рассмотренным выше задачам Коши.
|
|