
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы молекулярной динамики
|
|
Молекулярная динамика (МД) - это метод компьютерного моделирования, позволяющий проследить эволюцию системы взаимодействующих атомов во времени с помощью интегрирования уравнений движения. Область применимости молекулярной динамики определяется доступными компьютерными мощностями и сложностью законов, используемых для описания межатомного взаимодействия. Характерные длительности процессов, моделируемых с помощью МД, лежат в диапазоне от нескольких пикосекунд до десятков наносекунд. С макроскопической точки зрения даже наиболее длительные достижимые для МД времена крайне малы. Поэтому наиболее успешно МД применяется для описания быстропротекающих процессов.
В материаловедческих приложениях, МД применяется для изучения динамики кристаллической решетки материалов, моделирования различных дефектов кристаллической структуры: от точечных (вакансии, дефекты внедрения) до линейных (дислокации) и плоских (межфазные границы, доменные границы и т.д.), исследования кинетики перемещения дефектов и примесных атомов по объему материала и кинетики взаимодействия дефектов между собой. Несомненным достоинством метода МД является возможность моделирования атомных ансамблей, как в условиях термического равновесия, так и при нетермодинамических быстропротекающих процессах (например, при образовании каскадов атомных столкновений при облучении или ионной имплантации).
Метод молекулярной динамики по сравнению с другими методами компьютерного моделирования обладает несколькими полезными особенностями. Во-первых, он позволяет решать задачи структурно-энергетических трансформаций, как в кристаллических, так и в некристаллических материалах. Во-вторых, он дает возможность соизмерять динамику исследуемых процессов с реальным временем. Главным недостатком метода являются большие затраты машинного времени, требуемые для выполнения расчетов.
Основы метода молекулярной динамики. В методе молекулярной динамики поведение заданной совокупности атомов описывается в рамках классической механики системой простых дифференциальных уравнений движения в форме Ньютона, численное решение которых осуществляется на компьютере. Рассмотрим классическую систему, которая, в общем случае, может содержать от нескольких десятков до сотен тысяч частиц с заданным потенциалом взаимодействия между ними. Второй закон Ньютона для произвольного атома i моделируемого кристаллита, состоящего из N атомов, записывается как:
 , (14.20)
, (14.20)
Можно видеть, что пространственное положение 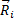 любого из атомов может быть определено в любой момент времени, если известна масса атома mi; и силы
любого из атомов может быть определено в любой момент времени, если известна масса атома mi; и силы 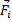 , действующие на атом в результате его взаимодействия с окружающими атомами. Для однозначности решения системы дифференциальных уравнений второго порядка необходимо задать исходные координаты атомов кристаллита и их скорости.
, действующие на атом в результате его взаимодействия с окружающими атомами. Для однозначности решения системы дифференциальных уравнений второго порядка необходимо задать исходные координаты атомов кристаллита и их скорости.
Формально, молекулярная динамика относится к классу детерминистических методов: при однозначно определенных (заданных) начальных координатах и скоростях атомов, последующая временная эволюция атомной системы, в принципе, полностью определена. Вычисляется траектория в 6N -мерном фазовом пространстве (3N позиций и 3N импульсов). Однако, траектория сама по себе, как правило, не представляет для исследователей особого интереса. Чаще, молекулярная динамика используется в качестве метода статистической механики, что оправдано для эргодических систем. Для таких систем усреднение некоторой физической величины по времени совпадает с ее усредненным значением по множеству конфигураций, распределенных согласно некоторой статистической функции распределения, или статистическому ансамблю. Траектория, получаемая при помощи метода молекулярной динамики, предоставляет информацию о таком наборе конфигураций. Таким образом, определение физических величин с помощью моделирования методом МД сводится к вычислению среднеарифметического значения набора различных мгновенных значений, приобретаемых данной величиной за время моделирования.
Метод МД может быть использован, в частности, для изучения термодинамических свойств материалов, с использованием подходов статистической физики, как связующего звена между описанием поведения системы на микроскопическом уровне и термодинамики. В пределе больших времен моделирования, можно ожидать, что фазовое пространство будет полностью просканировано и что процесс статистического усреднения даст на выходе описание термодинамических свойств системы. На практике, длительность одного запуска моделирования всегда имеет некую конечную величину поэтому, прежде всего, необходимо оценить, когда выборка значений достигает стационарного состояния.
Молекулярная динамика очень мощная методика, но есть ограничения, которые следует учитывать при интерпретации полученных результатов. Прежде всего, MД, как никакая другая методика, чувствительна к выбору способа описания межатомных взаимодействий (межатомного потенциала взаимодействия). В молекулярной динамике, атомы движутся под действием мгновенной силы, результата взаимодействия атомов друг с другом. Как уже говорилось ранее, эти силы, как правило, получают как градиенты функции потенциальной энергии, которая зависит от положения атомов. По мере перемещения атомов, их относительные смещения и, соответственно, силы изменяются. Реалистичное моделирования – это моделирование, которое способно имитировать поведение реальной системы. т. е. в котором силы межатомного взаимодействия похожи на те, с которыми реальные атомы (или, точнее, ионы) будут взаимодействовать, когда элементы системы расположены в той же конфигурации. Поэтому степень реалистичности моделирования системы зависит от способности выбранного потенциала межатомного взаимодействия воспроизвести поведение материала в условиях, при которых моделирование выполняется. По этой причине многие работы в области компьютерного моделирования посвящены разработке соответствующих потенциалов. В большинстве случаев используемые потенциалы относятся к разряду “классических”, поскольку расчет межатомных сил взаимодействия из “первых принципов” в рамках МД требуют существенно более серьезных вычислительных мощностей. В этом случае типичное МД моделирование может быть выполнено для систем, содержащих тысячи и, может быть, миллионы атомов, и временного интервала от нескольких пикосекунд до сотен наносекунд.
Моделирование может считаться надежным с точки зрения временного интервала, когда " внутреннее" время моделирования (то есть - значение временного параметра t в конце моделирования) значительно превышает время релаксации изучаемых величин. Например, в случае моделирования диффузионных процессов, отдельные диффузионные скачки атомов являются редкими событиями, и t моделирования наносекундного диапазона позволяет, как правило, наблюдать всего несколько таких скачков. С другой стороны, для того, чтобы следовать атомной траектории и при этом удерживать температуру кристалла близкой к среднему значению, продолжительность шага " внутреннего" времени, как правило, выбирается равной нескольким фемтосекундам (10-15 с). Поэтому типичное МД моделирование требует 106-107 итераций, что предполагает использования большого количества процессорного времени при моделировании достаточно больших кристаллов. В результате, определение коэффициентов диффузии (а также энергии миграции, определенные из температурных зависимостей коэффициентов диффузии) методом молекулярной динамики требует дополнительных приемов, которые бы позволили построить достаточно длинные траектории.
Ограничение на размер моделируемой системы также может представлять собой проблему. В этом случае необходимо сравнить размер МД ячейки с длиной затухания пространственных корреляционных функций, представляющих интерес. При длине корреляций сравнимой с размером расчетной ячейки, результаты не надежны. Эту проблему можно частично решить с помощью метода, известного как масштабирование конечного размера. Его идея состоит в расчете некоторой физической величины A, используя несколько различных размеров расчетной ячейки L, а затем экстраполировании полученных результатов на большие размеры ячейки с использованием экстраполяционного соотношения
 (14.21)
(14.21)
где A0, A1, и n используются как экстраполяционные параметры. Тогда A0 – соответствующий предел значений A(L), когда L стремится к бесконечности, может быть принято как наиболее надежная оценка для “истинного”' значения физической величины.
При моделировании, например, диффузионных процессов ограничение на размер атомного ансамбля является важным фактором. Даже 106 атомов в расчетной ячейке представляют собой весьма небольшую часть реального кристалла и поэтому необходимо определить соответствующие граничные условия для того, чтобы имитировать взаимодействия атомов вблизи границы расчетной ячейки с остальным материалом. В МД моделировании часто используются периодические граничные условия. Использование периодических граничных условий не позволяет использовать расчетные ячейки малого размера, для которых упругое взаимодействие диффундирующих частиц с атомами вне расчетной ячейки (атомами “отображения”) играет важную роль. В этом случае, использование периодических граничных условий может привести к фиктивной локализации диффундирующих частиц вблизи периодической границы из-за накопления систематических расчетных ошибок. Частота диффузионных скачков также может зависеть от расстояния диффундирующих частиц от границы расчетной ячейки, что является чисто вычислительным артефактом, связанным с необходимостью учета взаимодействия с атомами отображения.
Типичная последовательность шагов для МД моделирования включает в себя:
- Создание модели кристалла;
- Релаксация полученной системы статическими или квази-динамическими методами, с использование предполагаемых межатомных потенциалов;
- При необходимости – предварительный нагрев расчетной ячейки до желаемой температуры и выдержка при этой температуре (в пределах нескольких пикосекунд) для доастижения моделируемой системой термодинамического равновесия;
- Моделирование траектории системы в фазовом пространстве при постоянных или переменных внешних условиях (температура, объем расчетной ячейки, давление и т.п.).
Алгоритмы интегрирования уравнений движения. Используемые алгоритмы интегрирования уравнений Ньютона, как правило, основаны на методе конечных разностей, где время дискретизации на сетке конечно, а расстоянием между соседними точками на сетке является шаг по времени  . Исходя из атомных координат и скоростей в момент времени t, схема интегрирования позволяет определить эти величины в момент времени
. Исходя из атомных координат и скоростей в момент времени t, схема интегрирования позволяет определить эти величины в момент времени  . Повторяя процедуру, можно проследить эволюцию системы во времени.
. Повторяя процедуру, можно проследить эволюцию системы во времени.
При выборе алгоритма интегрирования, важно помнить, что каждый итерационный шаг привносит расчетную ошибку и, таким образом, алгоритм должен гарантировать, что десятки миллионов итераций не приведут к существенной потере точности. Существует два основных источника расчетных ошибок. Первый из них связан с точностью, с которой метод конечных разностей приближает истинное решение. Конечно-разностные методы, как правило, основаны на разложении в ряд Тейлора. Поэтому эти ошибки являются неотъемлемой частью алгоритма и не зависят от конкретной реализации. Точность аппроксимации обычно достигается путем выбора надлежащего небольшого шага интегрирования  . Например, в алгоритм Верле такого рода ошибки пропорциональны
. Например, в алгоритм Верле такого рода ошибки пропорциональны  для каждого шага интегрирования по времени. Другой источник ошибок может быть связан с конкретной реализацией алгоритма (например - с конечным числом значащих цифр в представлении нецелых чисел). Ошибки округления уменьшаются с уменьшением
для каждого шага интегрирования по времени. Другой источник ошибок может быть связан с конкретной реализацией алгоритма (например - с конечным числом значащих цифр в представлении нецелых чисел). Ошибки округления уменьшаются с уменьшением  медленнее, чем погрешности аппроксимации, и являются доминирующими в пределе малых
медленнее, чем погрешности аппроксимации, и являются доминирующими в пределе малых  . Использование 64-разрядной точности в процессе численной реализации алгоритма итегрирования (что соответствует " двойной точности'' при использовании, например, языка FORTRAN) помогает существенно уменьшить ошибки округления.
. Использование 64-разрядной точности в процессе численной реализации алгоритма итегрирования (что соответствует " двойной точности'' при использовании, например, языка FORTRAN) помогает существенно уменьшить ошибки округления.
Наиболее известными методами численного интегрирования в МД расчетах являются алгоритм Эйлера, алгоритм Верле и алгоритм «предиктор-корректор».
Если расчетная ячейка содержит N одинаковых атомов, то позиции и скорости всех атомов полностью характеризуются 2ζ N координатами (ζ – размерность расчетной ячейки). В методе Эйлера уравнения, записанные в конечных разностях, принимают вид:
 , (14.22)
, (14.22)
 (14.23)
(14.23)
где Δ t – шаг интегрирования.
В качестве критерия выбора шага интегрирования Δ t используют эмпирическое правило: флуктуации полной энергии системы не должны превышать флуктуации потенциальной энергии. Для уменьшения энергетических флуктуаций, на величину Δ t накладывают математические и физические ограничения. Математические ограничения обусловлены погрешностями округления, возникающими при выполнении арифметических операций. Физические связаны с тем, что шаг интегрирования должен быть, по крайней мере, меньше ¼ наименьшего периода атомных колебаний. В противном случае колебания атомов становятся апериодическими, что приводит к возрастанию энергии системы. Начальные значения координат атомов задаются в зависимости от исследуемой задачи, причем перекрывающиеся конфигурации исключаются. Начальные скорости атомов в простейшем случае задаются одинаковыми по абсолютной величине и со случайными направлениями. При этом полная кинетическая энергия должна соответствовать заданной температуре, а суммарный импульс расчетной ячейки должен быть равен нулю. Как правило, предполагается, что в термическом равновесии скорости атомов отвечают распределению согласно распределению Больцмана, так что
 ,
,  , (14.24)
, (14.24)
где k – постоянная Больцмана, T – температура, v кв – среднеквадратичная скорость атома. При решении задач молекулярной динамики осуществляется контроль над потенциальной U и кинетической E энергиями расчетной ячейки. Кинетическая энергия определяется как:
 . (14.25)
. (14.25)
Средняя температура расчетной ячейки находится из выражения
 . (14.26)
. (14.26)
Устойчивость численного решения можно контролировать в случае, когда моделирование проводится в предположении сохранения полной энергии и объема системы. В этом случае полная энергия в процессе моделирования не должна отклоняться от своего первоначального значения. Очевидно, что в результате накопления ошибок в процессе вычислений, сохранение энергии системы возможно только с некоторой точностью и все что возможно потребовать, это чтобы погрешность энергии, накопленная в процессе расчета, была достаточно мала. Как правило, алгоритм Эйлера не может обеспечить сохранение энергии при достаточно длительных расчетах.
Наиболее известным из методов, обеспечивающих более точное соблюдение закона сохранения энергии, является алгоритм Верле (Verlet). В литературе по численному анализу его часто называют неявной симметричной разностной схемой. В случае алгоритма Верле записываются два разложения Тейлора третьего порядка для атомных позиций  в моменты времени
в моменты времени 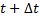 и
и  :
:
 (14.27)
(14.27)
где  обозначает третью производную координат по времени. Складывая эти два выражения, получаем основное выражение алгоритма Верле,
обозначает третью производную координат по времени. Складывая эти два выражения, получаем основное выражение алгоритма Верле,
 (14.28)
(14.28)
Так как мы интегрируем уравнения движения Ньютона, то ускорение частицы легко определяется через силы, которые, в свою очередь, являются функцией координат частицы  . Как можно сразу видеть, погрешность алгоритма, накапливающаяся за временной шаг эволюции системы
. Как можно сразу видеть, погрешность алгоритма, накапливающаяся за временной шаг эволюции системы  , порядка
, порядка  , т.е. алгоритм Верле обладает более высоким порядком точности по Δ t, чем алгоритм Эйлера. Несомненным достоинством данного алгоритма является простота его реализации, точность и устойчивость его работы, что и объясняет его большую популярность среди известных методов интегрирования уравнений молекулярной динамики.
, т.е. алгоритм Верле обладает более высоким порядком точности по Δ t, чем алгоритм Эйлера. Несомненным достоинством данного алгоритма является простота его реализации, точность и устойчивость его работы, что и объясняет его большую популярность среди известных методов интегрирования уравнений молекулярной динамики.
Определенным неудобством этой версии алгоритма Верле является то, что скорости частиц напрямую не генерируются, хотя часто бывают необходимы, например, для расчета кинетической энергии, проверки сохранения полной энергии и проверки устойчивости температуры в процессе моделирования. Скорость может быть вычислена, исходя из положений частиц, используя следующее выражение
 (14.29)
(14.29)
Однако, ошибки, связанные с этим выражением, порядка  , а не
, а не  . Еще одна проблема алгоритма Верле состоит в том, что атомные позиции определяются из двух предыдущих шагов по времени и, следовательно, этот алгоритм не может быть использован на первом шаге интегрирования. Поэтому, для первого шага используются другие методы такие как, например, скоростной алгоритм Верле, где положения, скорости и ускорения на шаге (t +Δ t) вычисляются следующим по формулам:
. Еще одна проблема алгоритма Верле состоит в том, что атомные позиции определяются из двух предыдущих шагов по времени и, следовательно, этот алгоритм не может быть использован на первом шаге интегрирования. Поэтому, для первого шага используются другие методы такие как, например, скоростной алгоритм Верле, где положения, скорости и ускорения на шаге (t +Δ t) вычисляются следующим по формулам:
 , (14.30)
, (14.30)
Преимуществом скоростной формы алгоритма Верле является то, что она является самостартующей.
Алгоритмы типа «предиктор-корректор» представляют собой другой класс методов интегрирования уравнений движения. Наиболее часто используемые в молекулярной динамике алгоритмы включают в себя три этапа на каждом временном шаге интегрирования: предсказание, оценка силы и коррекция. На этапе " предсказания” производится прогнозирование атомных координат и их производных по времени (включая и вторые производные - ускорение) в момент времени  . Прогнозирование производится, исходя из значений этих величин, известных для момента времени t с помощью разложения в ряд Тейлора. Этап “оценка сил” включает в себя вычисление сил, действующих на атомы, расположенных в предсказанных позициях, например, через расчет градиента потенциала взаимодействия. Полученные в результате величины ускорения, как это определено законом Ньютона, будут, в целом, отличается от «предсказанного» ускорения. Наличие разницы между ними является «сигналом ошибки». На этапе «корректировки» полученный сигнал ошибки используется для поправки атомных позиций и их производных. Все поправки пропорциональны сигналу ошибки, коэффициент пропорциональности является " магическим числом'' и определяется таким образом, чтобы алгоритм был максимально устойчивым.
. Прогнозирование производится, исходя из значений этих величин, известных для момента времени t с помощью разложения в ряд Тейлора. Этап “оценка сил” включает в себя вычисление сил, действующих на атомы, расположенных в предсказанных позициях, например, через расчет градиента потенциала взаимодействия. Полученные в результате величины ускорения, как это определено законом Ньютона, будут, в целом, отличается от «предсказанного» ускорения. Наличие разницы между ними является «сигналом ошибки». На этапе «корректировки» полученный сигнал ошибки используется для поправки атомных позиций и их производных. Все поправки пропорциональны сигналу ошибки, коэффициент пропорциональности является " магическим числом'' и определяется таким образом, чтобы алгоритм был максимально устойчивым.
Статистические ансамбли. При использовании методов молекулярной динамики для описания термодинамических свойств атомных систем необходимо учитывать особенности, характерные для различных термодинамических ансамблей. В статистической физике различаются 4 основных вида статистических ансамблей:
1. Микроканонический ансамбль, в котором сохраняющимися величинами являются число частиц N, объем V и внутренняя энергия E (или так называемая NVE-ансамбль).
2. Канонический ансамбль, в котором сохраняются число частиц N, объем V и температура T (NVT- ансамбль).
3. Изотермо-изобарический ансамбль с постоянными числом частиц N, давлением P и температурой T (NPT- ансамбль).
4. Большой канонический ансамбль с постоянным химическим потенциалом m, объемом V и температурой T (mPT- ансамбль).
Каждый ансамбль характеризуется набором заданных термодинамических величин (отраженных в названиях ансамблей), тогда как остальные величины определяются усреднением по ансамблю. Соответственно, для каждого мгновенного состояния системы значения этих величин отличаются от средних (флуктуируют).
Методы интегрирования уравнений движения, рассмотренные выше, обеспечивают (с разумной точностью) сохранение энергии системы. Объем расчетной ячейки и число частиц в ней также часто постоянны, что соответствует микроканоническому ансамблю. Однако МД позволяет проводить моделирование и в других ансамблях (чаще всего NVT и NPT). В таких ансамблях вместо полной энергии требуется поддерживать на более-менее постоянном уровне температуру системы атомов, а в случае NPT ансамбля – еще и давление.
Различают 4 основных способа поддержания постоянной термодинамической величины:
Дифференциальный, когда величина имеет строго фиксированное значение, и флуктуации около среднего отсутствуют.
Пропорциональный, когда величины, связанные с термодинамической величиной f, корректируются на каждом шаге интегрирования с использованием поправочного коэффициента, устанавливающего заданное значение f. Поправочный коэффициент определяет величину флуктуаций вокруг < f >.
Интегральный, когда гамильтониан системы расширяется путем включения новых независимых величин, которые отражают эффект внешней среды, фиксирующей состояние желаемого ансамбля. Эволюция во времени этих величин описывается уравнениями движения, полученными из расширенного гамильтониана.
Стохастический, когда значения величин, связанных с термодинамической величиной f, присваиваются в соответствии с модифицированными уравнениями движения, в которых некоторые степени свободы дополнительно изменяются стохастически, чтобы придать желаемое среднее значение величине f.
Молекулярная динамика при постоянной температуре. Прежде чем рассмотреть алгоритмы моделирования при постоянной температуре, вспомним, что означает “постоянная температура”. Температуру некоторой системы можно установить, приводя ее в тепловой контакт с большим тепловым резервуаром. В этих условиях вероятность нахождения системы в том или ином энергетическом состоянии определяется распределением Больцмана, а скорости (импульсы) распределены по закону Максвелла-Больцмана
 . (14.31)
. (14.31)
При таком распределении между средней кинетической энергией и температурой имеет место соотношение
 . (14.32)
. (14.32)
Алгоритмы, обеспечивающие поддержание средней кинетической энергии на уровне, соответствующем некоторой заданной температуре, обычно называю «термостатами».
1. Термостат Андерсена (стохастический метод). В методе Андерсена для поддержания постоянной температуры система “приводится в контакт” с тепловым резервуаром, который задает желаемую температуру. Этот контакт моделируется путем придания случайных импульсов случайно выбранным частицам системы, то есть столкновения выбранных частиц с виртуальными частицами. Можно показать, что термостат Андерсена воспроизводит канонический ансамбль.
Алгоритмическая реализация термостата Андерсена состоит из следующих шагов:
Начиная с исходного состояния, заданного совокупностью начальных координат и импульсов, интегрируются уравнения движения системы для некоторого интервала времени  .
.
Выбирается некоторая часть частиц, которые должны испытать столкновения с резервуаром.
Скорости выбранных частиц устанавливаются в соответствии с распределением Максвелла, соответствующего желаемой температуре. Остальные частицы не испытывают влияния этих столкновений.
Стохастические столкновения частиц системы с резервуаром “перекидывают” систему с одной изоэнергетической поверхности фазового пространства на другую. Между столкновениями система эволюционирует при постоянной энергии. Таким образом, стохастические столкновения обеспечивают пребывание системы во всех доступных энергетических состояниях в соответствии с их больцмановским весом.
В одной из реализаций метода вводится параметр связи, характеризующий степень связи с внешним резервуаром. В этом подходе память частицы нарушается не полностью, а только частично. Новый импульс выбранной частицы полагается равным
 , (14.33)
, (14.33)
где  ‑ импульс, выбранный из распределения Максвелла. Параметр
‑ импульс, выбранный из распределения Максвелла. Параметр  может быть выбран так, чтобы давать микроканонический ансамбль при
может быть выбран так, чтобы давать микроканонический ансамбль при  и канонический при
и канонический при  .
.
2. Метод расширенной системы, или интегральный метод. Интегральный метод часто называется методом расширенной системы, так как он основан на введении в гамильтониан системы одной или нескольких дополнительной степени свободы, для которых также могут быть получены уравнения движения. Эти уравнения интегрируются вместе с уравнениями для пространственных координат и импульсов атомов. Тепловые взаимодействия между резервуаром и системой приводят к изменению кинетической энергии, то есть скоростей частиц. Поэтому формально оно может быть выражено пропорциональным изменением скоростей. Система с гамильтонианом, содержащим все переменные, описывает канонический ансамбль. В известной реализации этого метода, изобретенной Нозэ и развитой Гувером, влияние внешней системы описывается с помощью только одной дополнительной степени свободы.
3. Метод ограничивающих условий, или дифференциальный термостат. Для поддержания фиксированной температуры без флуктуаций был предложен ряд моделей. Первый метод этого рода был введен Вудкоком (Woodcock) и основан на умножении импульсов на поправочный коэффициент:  , где
, где  ‑ желаемая, а
‑ желаемая, а  ‑ мгновенная, определенная из скоростей частиц, температура. Этот метод приводит к разрывам в импульсной части фазовой траектории. Кроме того, слишком резкое изменение температуры на каждом шаге может вызвать большой шум в высокочастотной области фононного спектра системы. Поэтому часто умножение производится не на сам поправочный коэффициент, а на корень высокой степени от этого фактора. Например, в известной программе XMD по умолчанию скорости умножаются на корень 33-й степени от
‑ мгновенная, определенная из скоростей частиц, температура. Этот метод приводит к разрывам в импульсной части фазовой траектории. Кроме того, слишком резкое изменение температуры на каждом шаге может вызвать большой шум в высокочастотной области фононного спектра системы. Поэтому часто умножение производится не на сам поправочный коэффициент, а на корень высокой степени от этого фактора. Например, в известной программе XMD по умолчанию скорости умножаются на корень 33-й степени от  . Это приводит к установлению желаемой температуры в течение 33-х шагов.
. Это приводит к установлению желаемой температуры в течение 33-х шагов.
4. Пропорциональный термостат. Пропорциональный термостат стремится корректировать отклонения текущей температуры T от заданной Т 0 путем умножения скоростей на некоторый фактор l, чтобы заставлять дрейфовать динамику системы к той, которая соответствует Т 0. Отличие от дифференциального термостата заключается в том, что метод допускает флуктуации температуры, не фиксируя ее значения. На каждом шаге Т придается значение, более близкое к Т 0. Термостат этого типа был предложен Берендсеном (Berendsen) и др., которые ввели метод слабой связи с внешним резервуаром. Этот метод минимизирует локальные отклонения стохастического термостата, не меняя глобального эффекта. В этом методе импульсы преобразуются как  , где
, где
 , (14.34)
, (14.34)
где t ‑ временная константа связи, которая определяет масштаб времени, в течение которого достигается желаемая температура. Можно показать, что пропорциональный термостат сохраняет распределение Максвелла.
Молекулярная динамика при постоянном давлении. Алгоритмы поддержания постоянного давления часто называются «баростатами». Как легко понять, поддержание давление невозможно при сохранении полного объема расчетной ячейки, так что суть практически всех баростатов – это изменение объема и/или формы системы таким образом, чтобы среднее давление в системе оставалось примерно постоянным.
1.Метод расширенной системы. Этот метод был предложен Андерсеном (1980). Объем расчетной ячейки в этом подходе рассматривается как дополнительная свободная переменная. Это моделирует воздействие на систему поршня. Поршень имеет массу Q, которая имеет размерность кг/м4 и кинетическую энергией  . Потенциальная энергия, связанная с дополнительной переменной, равна
. Потенциальная энергия, связанная с дополнительной переменной, равна  , где P ‑ заданное давление. Лагранжиан системы содержит кинетические и потенциальные энергии как частиц, так и стенки ячейки, и с его помощью можно получить уравнения движения, включающие также изменение объема. Масса поршня Q является оптимизуруемым параметром. Малая масса приводит к слишком быстрым осцилляциям размеров ячейки, которые не очень эффективно демпфируются случайным движением частиц. Слишком большая масса приводит к медленному движению фазовой точки в пространстве объема.
, где P ‑ заданное давление. Лагранжиан системы содержит кинетические и потенциальные энергии как частиц, так и стенки ячейки, и с его помощью можно получить уравнения движения, включающие также изменение объема. Масса поршня Q является оптимизуруемым параметром. Малая масса приводит к слишком быстрым осцилляциям размеров ячейки, которые не очень эффективно демпфируются случайным движением частиц. Слишком большая масса приводит к медленному движению фазовой точки в пространстве объема.
2. Методы ограничивающих условий. Среди методов, использующих ограничивающие условия, наиболее простым методом является метод фиксация давления (англ. pressure clamp). На каждом шаге МД размеры расчетной ячейки автоматически изменяются для того, чтобы поддерживать постоянное давление. Для этого пользователь задает желаемое значение давления. На каждом шаге рассчитывается давление в системе. Исходя из этого давления и модуля сжатия, рассчитывается изменение объема ячейки, которое это давление компенсирует:
 , (14.35)
, (14.35)
где  ‑ размер ячейки в направлении i,
‑ размер ячейки в направлении i,  ‑ изменение этого размера,
‑ изменение этого размера,  ‑ напряжение в направлении i, B ‑ модуль всестороннего сжатия, а m ‑ параметр, контролирующий, как быстро алгоритм устанавливает нужный размер ячейки. Значение модуля всестороннего сжатия для конкретного моделируемого материала как правило берется равным экспериментальному.
‑ напряжение в направлении i, B ‑ модуль всестороннего сжатия, а m ‑ параметр, контролирующий, как быстро алгоритм устанавливает нужный размер ячейки. Значение модуля всестороннего сжатия для конкретного моделируемого материала как правило берется равным экспериментальному.
3.Изменение формы ячейки моделирования. Метод Андерсена допускает только изотропное изменение объема расчетной ячейки. Паринелло и Рамэн (Parinello, Rahman 1980-1982) доработали этот метод с тем, чтобы он допускал изменение не только размера, но также и формы ячейки. Эта степень свободы особенно важна при моделировании твердых тел, когда возможны фазовые переходы, изменяющие соотношения линейных размеров в различных направлениях и углы. В этом подходе дополнительная степень свободы связывается не только с объемом ячейки, но и с направлениями нормалей к ее граням. Соответственно, для этих переменных также записываются и решаются уравнения движения.
|
|