
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обобщенный метод наименьших квадратов
|
|
При наличии гетероскедастичности в остатках рекомендуется традиционный метод наименьших квадратов (МНК) заменять обобщенным методом наименьших квадратов (ОМНК).
Будем предполагать, что среднее значение остаточных величин равно нулю. А вот дисперсия их не остается неизменной для различных значений фактора, а пропорциональна некоторой величине 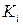 , т.е.
, т.е.
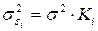 ,
,
где  - дисперсия ошибки на конкретном (i – ом) значении фактора;
- дисперсия ошибки на конкретном (i – ом) значении фактора;
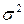 - постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
- постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
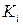 - коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обуславливает неоднородность дисперсии.
- коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обуславливает неоднородность дисперсии.
При этом полагается, что величина 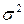 неизвестна, а в отношении величины
неизвестна, а в отношении величины 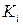 выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
В общем виде уравнение регрессии примет вид
 .
.
Исходные данные для этого уравнения будут иметь вид:
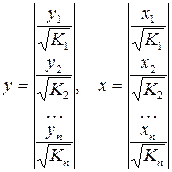 .
.
По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные x и y взяты с весами 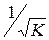 .
.
Оценка параметров нового уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для которого необходимо минимизировать сумму квадратов отклонений вида
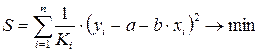 .
.
|
|