
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Часовий ряд.
|
|
Як було відмічено у попередньому підрозділі 4.2, використання засобів обчислювальної техніки при аналізі сигналів пов’язано з перетворенням неперервних сигналів в сигнали з дискретним часом, що приводить до розгляду часових рядів.
Під часовим рядом 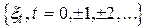 розуміють послідовність спостережень, як правило, впорядковану по часу.
розуміють послідовність спостережень, як правило, впорядковану по часу.
Одержаний часовий ряд 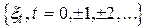 є вихідними даними для статистичного оцінювання характеристик досліджуваних випадкових процесів.
є вихідними даними для статистичного оцінювання характеристик досліджуваних випадкових процесів.
Основними видами статистичного аналізу вважається:
1. статистичне оцінювання;
2. перевірка статистичних гіпотез.
Статистичне оцінювання поділяють на параметричне та непараметричне. Параметричне оцінювання включає в себе:
а) точкове оцінювання;
б) інтервальне оцінювання.
Точкове оцінювання. Розглянемо досліджувану випадкову величину 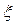 з відомою функцією розподілу
з відомою функцією розподілу 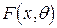 , де
, де  - деякий невідомий параметр. Задана послідовність результатів спостережень над
- деякий невідомий параметр. Задана послідовність результатів спостережень над 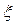 , тобто вибірка
, тобто вибірка 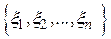 обсягу
обсягу 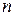 , яка залежить від невідомого параметра
, яка залежить від невідомого параметра  .
.
ОЗНАЧЕННЯ 4.4. Точковою оцінкою параметра  називають однозначно визначену функцію
називають однозначно визначену функцію  від результатів спостережень над випадковою величиною
від результатів спостережень над випадковою величиною 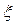 .
.
Точкове оцінювання полягає у виборі цієї функції таким чином, щоб її значення можна було прийняти за найкраще в даних умовах і в певному ймовірнісному розумінні наближення до параметра  для оцінюваної випадкової величини
для оцінюваної випадкової величини 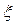 , наприклад, щоб її розподіл концентрувався навколо параметра
, наприклад, щоб її розподіл концентрувався навколо параметра  .
.
Точкова оцінка є функцією випадкових змінних  , а тому вона сама являє собою випадкову величину і називається вибірковою. Її можна охарактеризувати умовною функцією розподілу
, а тому вона сама являє собою випадкову величину і називається вибірковою. Її можна охарактеризувати умовною функцією розподілу 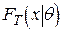 , а якщо випадкова величина
, а якщо випадкова величина 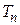 - неперервна, то й щільністю розподілу
- неперервна, то й щільністю розподілу 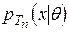 .
.
Функція розподілу ймовірностей 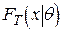 при заданій функції
при заданій функції 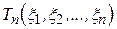 може бути одержана із заданої функції розподілу ймовірностей компонент вектора
може бути одержана із заданої функції розподілу ймовірностей компонент вектора 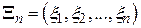 , яку позначимо через
, яку позначимо через 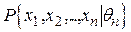 . Для цього невипадкову функцію
. Для цього невипадкову функцію 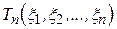 можна розглядати як деякий закон перетворення вектора
можна розглядати як деякий закон перетворення вектора 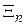 у випадкову величину
у випадкову величину 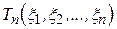 , а шукана щільність (при умові, що існує функція
, а шукана щільність (при умові, що існує функція 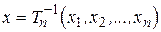 , обернена до функції
, обернена до функції  може бути отримана із заданої функції розподілу ймовірностей компонент вектора
може бути отримана із заданої функції розподілу ймовірностей компонент вектора 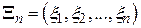 таким чином:
таким чином:
 (4.13)
(4.13)
де  множина в
множина в 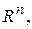 для якої
для якої 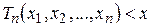 . Взагалі при записі вибіркової оцінки аргумент опускають і пишуть лише
. Взагалі при записі вибіркової оцінки аргумент опускають і пишуть лише 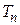 , дe
, дe 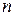 - обсяг вибірки. Іноді така оцінка доповнюється величиною дисперсії D
- обсяг вибірки. Іноді така оцінка доповнюється величиною дисперсії D 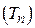 , як характеристикою похибки.
, як характеристикою похибки.
Відносно простими точковими оцінками є лінійні, що являють собою лінійні функції елементів вибірки.
Оскільки головна проблема теорії точкових оцінок полягає у виборі найкращої оцінки, то для здійснення такого вибору потрібно знати їх основні властивості. Зупинимося на деяких з них.
1. Вибіркова оцінка називається незсуненою (більш точно - незсуненою в середньому), якщо вона задовольняє співвідношенню
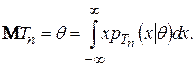 (4.14)
(4.14)
Фактично тут наведено умовне математичне сподівання, тобто прийнято 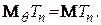
Іноді говорять, що незсунена оцінка дозволяє визначити параметр  без систематичної похибки.
без систематичної похибки.
В багатьох прикладних задачах часто на підставі вибірок достатньо знайти незсунені оцінки параметрів розподілу випадкової величини 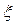 , таких як
, таких як  та D
та D 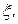 тобто середнє значення та дисперсію.
тобто середнє значення та дисперсію.
Зсувом оцінки називають різницю 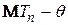 .
.
Якщо 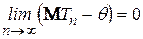 , то оцінка називається асимптотично незсуненою.
, то оцінка називається асимптотично незсуненою.
ПРИКЛАД 4.2. Незсуненою лінійною оцінкою для 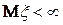 є середнє арифметичне від результатів спостережень над випадковою величиною
є середнє арифметичне від результатів спостережень над випадковою величиною 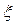 :
:
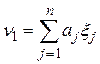 , де
, де 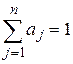 , (4.15)
, (4.15)
дійсно 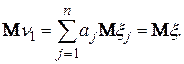
ПРИКЛАД 4.3. 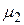 - вибірковий центральний момент другого порядку, визначається як
- вибірковий центральний момент другого порядку, визначається як
 , (4.16)
, (4.16)
тобто
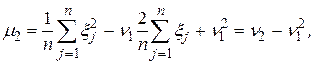
Далі маємо 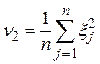 . Його математичне сподівання
. Його математичне сподівання
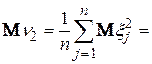
 D
D 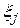 +
+ 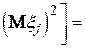 D
D 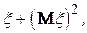
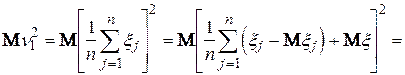
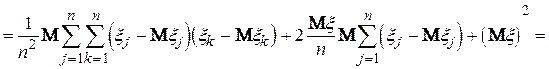
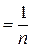 D
D 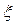
 .
.
Таким чином,
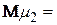 D
D 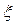 +
+  -
- 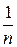 D
D 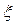 -
- 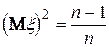 D
D 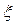 (4.17)
(4.17)
тобто  - є зсуненою оцінкою дисперсії
- є зсуненою оцінкою дисперсії 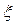 .
.
Користуватися незсуненими оцінками зручно, але однієї незсуненості мало, щоб вважати оцінку найкращою. Незсуненість вперше застосував Марков А.А. при обґрунтовуванні методу найменших квадратів.
2. Вибіркова оцінка параметра називається слушною, якщо при як завгодно малій величині  має місце наступне співвідношення:
має місце наступне співвідношення:
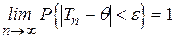 , (4.18)
, (4.18)
іншими словами, якщо вона збігається по ймовірності до  .
.
Ознака. Якщо оцінка 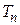 параметра
параметра  задовольняє наступним умовам:
задовольняє наступним умовам:
1. Є незсуненою або асимптотично незсуненою;
2.  D
D 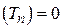 , то така оцінка називається слушною.
, то така оцінка називається слушною.
Цей факт випливає з нерівності Чебишева (див., наприклад [2, 4])
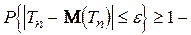
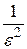 D
D 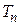 . (4.19)
. (4.19)
Останній вираз при 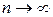 з врахуванням сформульованих вище умов доводить справедливість наведеного вище твердження.
з врахуванням сформульованих вище умов доводить справедливість наведеного вище твердження.
Середнє арифметичне 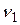 є слушною оцінкою тоді і лише тоді, коли вибіркові значення при
є слушною оцінкою тоді і лише тоді, коли вибіркові значення при 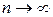 будуть некорельованими. Для випадку незалежних спостережень ця оцінка завжди слушна.
будуть некорельованими. Для випадку незалежних спостережень ця оцінка завжди слушна.
Якщо є декілька незсунених оцінок, то потрібно брати ту з них, яка має найменшу дисперсію.
ОЗНАЧЕННЯ 4.5. Незсунена вибіркова оцінка 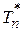 , яка має найменшу дисперсію серед усіх можливих незсунених оцінок параметра
, яка має найменшу дисперсію серед усіх можливих незсунених оцінок параметра  , розрахованих по
, розрахованих по 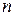 членах вибіркового ряду, називається ефективною оцінкою, тобто
членах вибіркового ряду, називається ефективною оцінкою, тобто
D 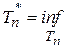 D
D 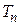 , (4.20)
, (4.20)
де 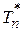 - ефективна оцінка, а
- ефективна оцінка, а 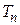 - довільна дійсна оцінка параметра
- довільна дійсна оцінка параметра  .
.
Якщо для дисперсій оцінок 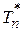 і
і 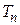 виконується умова
виконується умова
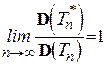 , (4.21)
, (4.21)
то оцінка 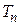 називається асимптотично ефективною.
називається асимптотично ефективною.
Зокрема, для незалежних спостережень дисперсія ефективної оцінки визначається виразом

 , (4.22)
, (4.22)
де  - кількість інформації на одне спостереження. В неперервному випадку її можна представити у вигляді
- кількість інформації на одне спостереження. В неперервному випадку її можна представити у вигляді
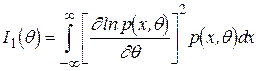 , (4.23)
, (4.23)
а в дискретному випадку
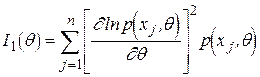 . (4.24)
. (4.24)
В неперервному випадку 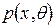 - щільність розподілу ймовірностей, а в дискретному
- щільність розподілу ймовірностей, а в дискретному 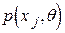 - розподіл ймовірностей.
- розподіл ймовірностей.
Функцію  Р.А.Фішер (1922-1925 р.р.) назвав інформацією, що знаходиться у вибірці. Якщо є два незалежних ряди спостережень, то інформація в них визначається сумою
Р.А.Фішер (1922-1925 р.р.) назвав інформацією, що знаходиться у вибірці. Якщо є два незалежних ряди спостережень, то інформація в них визначається сумою
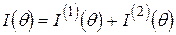 .
.
ПРИКЛАД 4.4. 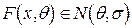 ,
,  - відомо, оцінити
- відомо, оцінити  . Оцінку
. Оцінку  знаходимо за допомогою виразу
знаходимо за допомогою виразу
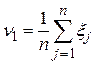 .
.
Згідно формули (4.23) маємо
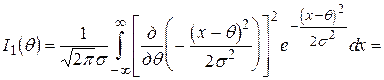


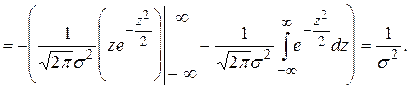
З іншого боку
D  D
D 
 D
D 
Порівнюючи ці два результати, робимо висновок, що
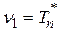 ,
,
тобто 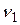 - є ефективною оцінкою
- є ефективною оцінкою  , якщо розподіл
, якщо розподіл 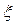 - нормальний.
- нормальний.
4. Статистична оцінка 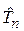 параметра
параметра  називається достатньою, якщо для довільної іншої оцінки
називається достатньою, якщо для довільної іншої оцінки 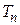 умовна випадкова величина
умовна випадкова величина 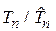 має розподіл, що не залежить від
має розподіл, що не залежить від  , тобто поява
, тобто поява 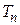 не дає нічого нового для оцінювання параметра
не дає нічого нового для оцінювання параметра  в порівнянні з тим, що отримується при появі
в порівнянні з тим, що отримується при появі 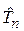 . Іншими словами, при заміні
. Іншими словами, при заміні 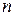 - вимірної системи координатного простору спостережень
- вимірної системи координатного простору спостережень 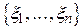 на нову
на нову 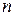 - вимірну систему з першою координатою
- вимірну систему з першою координатою 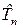 , а інші довільно взяті з вказаного вектора, вся інформація залишається лише у першій координаті.
, а інші довільно взяті з вказаного вектора, вся інформація залишається лише у першій координаті.
Незсуненість та ефективність вперше використовував А.А. Марков (1856-1922 р.р.), а слушність та достатність введені Р.А.Фішером (1922-1925 р.р.).
Інтервальне оцінювання. Формулювання задачі інтервального оцінювання будується на початку аналогічно до постановки задачі точкового оцінювання.
ОЗНАЧЕННЯ 4.6. Довірчим інтервалом  для невідомого параметра
для невідомого параметра  називають такий інтервал, відносно якого можна з раніш визначеною ймовірністю
називають такий інтервал, відносно якого можна з раніш визначеною ймовірністю 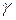 стверджувати, що він містить невідоме нам значення параметра
стверджувати, що він містить невідоме нам значення параметра  .
.
Таким чином, при інтервальному оцінюванні по Нейману, оцінюваний параметр  вважається невипадковим, в той час як
вважається невипадковим, в той час як 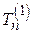 та
та 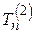 - межі довірчого інтервалу, являють собою випадкові величини, тобто функції від результатів спостережень
- межі довірчого інтервалу, являють собою випадкові величини, тобто функції від результатів спостережень 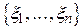 ;
; 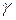 називається довірчим коефіцієнтом, він вибирається близьким до 1.
називається довірчим коефіцієнтом, він вибирається близьким до 1.
ПРИКЛАД 4.5. Припустимо, що є вибірка з незалежними елементами  , для оцінки математичного сподівання нормальної випадкової величини, у якої відома дисперсія
, для оцінки математичного сподівання нормальної випадкової величини, у якої відома дисперсія 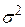 , тобто
, тобто  . Побудувати довірчий інтервал з заданим довірчим коефіцієнтом
. Побудувати довірчий інтервал з заданим довірчим коефіцієнтом 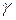 .
.
Неважко бачити, що в цьому випадку випадкова величина 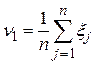 також має нормальний розподіл
також має нормальний розподіл  . Це можна довести, використовуючи поняття характеристичної функції:
. Це можна довести, використовуючи поняття характеристичної функції:
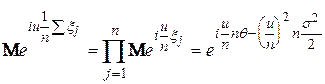 .
.
Тому нормовані відхилення 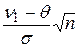 мають стандартний нормальний розподіл
мають стандартний нормальний розподіл 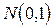 , для якого є таблиці, що дають змогу знаходити значення границь інтервалу із співвідношення
, для якого є таблиці, що дають змогу знаходити значення границь інтервалу із співвідношення
 .
.
Наприклад, при  , при
, при 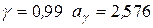 .
.
Вираз у фігурних дужках можна перетворити так, щоб у середньому члені залишилось лише  , а саме
, а саме
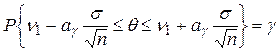 ,
,
звідки можна відразу виписати шукані межі довірчого інтервалу:

Половина довжини інтервалу  при заданому
при заданому 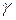 легко дозволяє обчислити необхідний обсяг вибірки для досягнення заданої точності при статистичній обробці за методом довірчих інтервалів в умовах цієї задачі.
легко дозволяє обчислити необхідний обсяг вибірки для досягнення заданої точності при статистичній обробці за методом довірчих інтервалів в умовах цієї задачі.
Доповнимо цей приклад числами. Знайти при 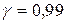 і відповідно
і відповідно  довірчий інтервал для оцінки кута цілі на площині по вибірці з 9-ти вимірювань, отриманих різними рівноточними методами (середньоквадратичне відхилення
довірчий інтервал для оцінки кута цілі на площині по вибірці з 9-ти вимірювань, отриманих різними рівноточними методами (середньоквадратичне відхилення 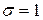 ), якщо були отримані наступні результати вимірювань (див. таблиця 4.1):
), якщо були отримані наступні результати вимірювань (див. таблиця 4.1):
Таблиця 4.1
Номер експерименту
| |||||||||
Результати
вимірювань 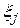
| +3 | +1 | -2 | +4 | +2 | +4 | -2 | +5 | +3 |
Знаходимо

Таким чином, 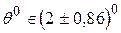 з ймовірністю
з ймовірністю 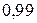 .
.
Контрольні запитання
1. Дати приклад стаціонарного випадкового процесу і навести його основні властивості.
2. Визначити слабо стаціонарний випадковий процес і дати приклади таких процесів.
3. Визначити одновимірну функцію розподілу, щільність розподілу, характеристичну функцію, математичне сподівання стаціонарного процесу.
4. Визначити двовимірну функцію розподілу, щільність розподілу та характеристичну функцію стаціонарного процесу.
5. Визначити дисперсію, коваріаційну та кореляційну функцію стаціонарного процесу.
6. Дати означення спектральної функції, спектральної щільності потужності стаціонарного процесу, визначити їх властивості, розклад на компоненти, зв’язок з автокореляційною функцією.
7. Зробити аналіз відгуку RLC- контуру при дії білого шуму в рамках кореляційної теорії.
8. Навести означення часового ряду як реалізації випадкового ряду; як послідовності випадкових величин; як послідовності незалежних випадкових величин, які мають один і той же закон розподілу ймовірностей.
9. Як задати закон розподілу часового ряду: послідовність функцій розподілу; таблиці ймовірностей; послідовність характеристичних функцій?
10. Визначити моментні функції часового ряду: початкові, центральні змішані.
11. Дати означення стаціонарних часових рядів: стаціонарних та слабо стаціонарних (стаціонарних в широкому розумінні).
12. Навести теорему для стаціонарного часового ряду, яка аналогічна теоремі Хінчина для неперервного стаціонарного випадкового процесу. Що спільного для цих теорем, які відмінності між ними?
13. Навести означення спектральної щільності, спектральної функції стаціонарного часового ряду, дати їх основні властивості.
14. Дати означення терміну “статистична оцінка” параметра функції розподілу.
15. На прикладі гауссового розподілу випадкової величини показати, які параметри потрібно оцінювати.
16. Назвати основні види статистичного оцінювання і навести приклади.
17. Які основні властивості статистичної оцінки?
18. При яких умовах середнє арифметичне вибірки обсягу 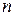 є статистичною оцінкою математичного сподівання? Які властивості такої оцінки і для яких випадкових функцій?
є статистичною оцінкою математичного сподівання? Які властивості такої оцінки і для яких випадкових функцій?
19. Які властивості асимптотичних статистичних оцінок?
20. Навести формули обчислення статистичної оцінки:
а) зсуненої;
б) незсуненої.
21. Наведіть визначення терміну “довірчий інтервал” невідомого параметра з використанням характерного прикладу.
22. На прикладі гауссового закону розподілу знайти межі довірчого інтервалу, коли:
а) 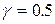 ;
;
б) 
23. Яким чином проводиться обґрунтування довірчого коефіцієнта 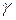 ?
?
|
|