
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель популяций Мальтуса
|
|
Лабораторная работа 1 ММ
Моделирование простейших систем
Модель математического маятника
Справочный материал
Рассмотрим модель математического маятника, используемая для определения скорости пули (Рис. 1):
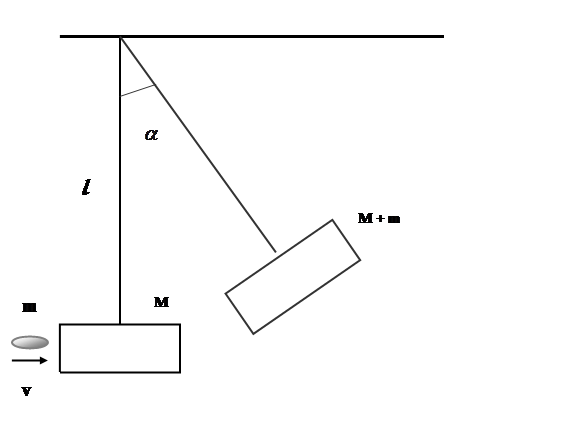
Рис. 1.
Здесь: M – масса маятника, m – масса пули, l – длина маятника,
α – угол отклонения маятника. Скорость пули v, рассчитанная на основе этой модели, вычисляется по формуле:
v= 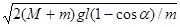
Пример. Пусть M = 60 кг =60000 г, m = 9 г, l = 2 м, g = 9.8 м/с2, α = 600,
Тогда по формуле (1) для скорости пули получаем величину
v =  .
.
Отсюда получаем v= 361 м/с.
Задание. По заданным величинам M, m, l, α рассчитать величину скорости пули v:
| №№ варианта | Масса маятника M (кг) | Масса пули m(г) | Длина маятника l (м) | Угол отклонения маятника (град) |
| 2.1 | ||||
| 2.0 | ||||
| 1.9 | ||||
| 1.8 | ||||
| 2.1 | ||||
| 2.2 | ||||
| 2.3 | ||||
| 2.4 | ||||
| 2.5 | ||||
| 1.9 | ||||
| 1.8 | ||||
| 1.7 | ||||
| 1.8 | ||||
| 1.9 | ||||
| 2.1 | ||||
| 2.3 | ||||
| 2.4 | ||||
| 2.2 | ||||
| 2.5 | ||||
| 2.1 |
Модель популяций Мальтуса
Справочный материал
В основу модели популяций Мальтуса положено простое утверждение - скорость изменения населения со временем t пропорциональна его текущей численности N(t), умноженной на сумму
коэффициентов рождаемости 
 и смертности
и смертности 
 . В результате приходим к уравнению
. В результате приходим к уравнению
 .
.
Задание. Проинтегрировать это соотношения при постоянных значениях α (t)=α и β (t)=β и начальном условии N(0)= 100, построить графики функций N(t) при значениях величин α и β из таблицы
| №№ варианта | α | β |
| 0.5 | ||
| 0.5 | ||
| 9.9 | ||
| 9.5 | ||
3. Модель «хищник - жертва»
Справочный материал
Математическая модель наиболее простой, т. е. двух видовой системы «хищник – жертва» основывается на следующих предположениях:
1) численности популяций жертв N и хищников M зависят только от времени (модель не учитывающая пространственное распределение популяции на занимаемой территории);
2) в отсутствие взаимодействия численность видов изменяется по модели Мальтуса; при этом число жертв увеличивается, а число хищников падает, так как им в этом случае нечем питаться:
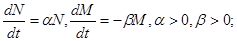
3) естественная смертность жертвы и естественная рождаемость хищника считаются несущественными;
4) эффект насыщения численности обеих популяций не учитывается;
5) скорость роста численности жертвы уменьшается пропорционально численности хищников, т. е. величине Cm, c> 0, а темп роста хищников увеличивается пропорционально численности жертвы, т. е. величине Dn, d> 0.
Объединяя предположения 1) – 5), приходим к системе уравнений Лотки

(1)
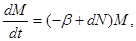
из которой по начальным численностям N(0), M(0) определяется численность популяций в любой момент t > 0.
Нелинейную систему (1) удобно исследовать в плоскости переменных N, M, для чего первое уравнение поделим на второе:
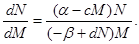 (2)
(2)
Уравнения (1), (2) имеют положение равновесия (или стационарное, не зависящее от времени решение):
M0 = 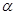 /c, N0 =
/c, N0 = 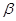 /d. (3)
/d. (3)
Исследуем устойчивость положения равновесия (3). Под этим подразумевается следующее. Если начальные численности в точности равны величинам (3), то как с течением времени они изменяются? Если по каким-то причинам численности ненамного отклоняются от величин M0, N0, то вернется ли система в положение равновесия? Наконец, если начальные значения N(0), M(0) заметно отличаются от равновесных, то каким образом они меняются со временем относительно величин N0, M0?
Для ответа на эти вопросы преобразуем уравнение (2) к виду
dn(- 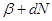 )M = dm(
)M = dm( 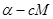 )N
)N
или, после деления на NM и переноса всех членов в левую сторону, к виду
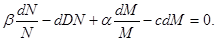 (4)
(4)
Уравнение (4) нетрудно проинтегрировать и получить соотношение
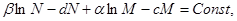
где константа в правой части определяется по начальным значениям N(0) M(0). Другими словами, уравнение (2), или, что то же самое, система (1) имеет интеграл вида
N 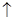
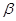 exp(-Dn)=C1 M
exp(-Dn)=C1 M 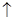 (-
(- 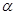 )exp(Cm), C1 > 0. (5)
)exp(Cm), C1 > 0. (5)
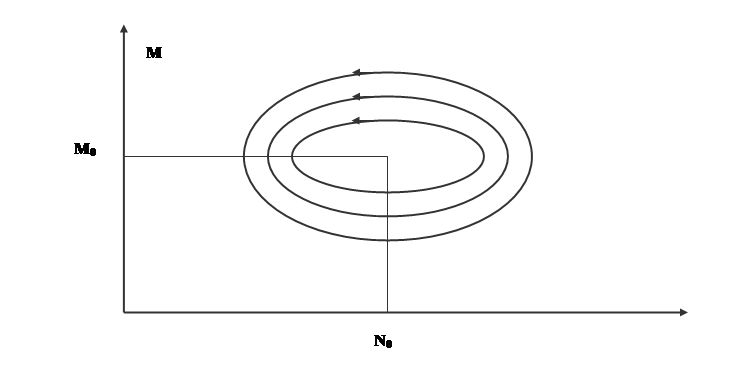
Существование интеграла (5) дает возможность ответить на поставленные выше вопросы (на Рис. 2 изображены фазовые траектории системы (1); направление движения по траекториям с течением времени – против часовой стрелки):

|
Рис. 2. Фазовые траектории системы «хищник-жертва»
а) если N(0)=N0, M(0)=M0, то во все моменты времени численности популяций не меняются;
б) при малом отклонении от положения равновесия численности как хищников, так и жертв с течением времени не возвращаются к равновесным значениям (при этом из модели (1) получается стандартное уравнение колебаний);
в) если отклонение от положения равновесия велико, то поведение функций N(t), M(t) такое же, как и в случае б).
Эти выводы означают, что численности популяций жертв и хищников совершают периодические колебания вокруг положения равновесия. Амплитуда колебаний и их период определяются начальными значениями численностей N()0, M(0), они совершаются не в фазе: максимальному значению N(t) соответствует среднее значение M(t) и наоборот.
Задание. Решить численно в окрестности положения равновесия
систему дифференциальных уравнений (1), начальные значения выбирать вблизи положения равновесия, шаг интегрирования выбирать равным одной десятой от равновесных значений M(0) и N(0), интервал интегрирования выбирать не менее, чем период колебаний. Построить графики N(t) и M(t). Значения величин α, β, c, d, необходимые для конкретизации системы (1), приведены в таблице:
| №№ варианта | α | β | c | d |
|
|