Двохвильова дифракція в ідеальному кристалі.

При розсіянні в кристалі монохроматичного рентгенівського випромінювання довжинами хвиль l порядку міжатомних відстаней (l~1Å), як правило, виникає обмежене число дифракційних хвиль, що мають помітну інтенсивність. Пов’язано це з тим, що при l»d умова дифракції (1.16) накладає досить жорсткі умови на можливі значення 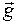, оскільки 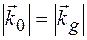і одночасно 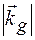, 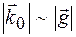. В результаті завжди можна реалізувати ситуацію, коли в кристалі наряду з заломленою хвилею хвильового вектору 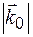є тільки одна дифракційна хвиля із хвильовим вектором 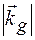. Оскільки амплітуди тільки цих двох хвиль відмінні від нуля, із всієї системи (1.20) слідує зберегти тільки ті два рівняння, які описують реально існуючі дифракційні хвилі в кристалі, тобто ми приходимо до двохвильової дифракційної задачі. Як правило на практиці використовуються пластини, які за двома розмірами можна вважати безмежними, наприклад в напрямку вісі х та у, і кінечні по вісі z.

Оскільки в двопроменевій задачі вектори 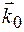, 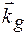і 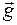знаходяться в одній площині (площині дифракції), то зручно ввести двомірну систему координат (x, z). В загальному випадку ця система може складати з вихідною поверхнею кристалу кут j. Дія подвійного векторного добутку в (1.20) для двохвильової дифракції зводиться до появи поляризаційного множника С:

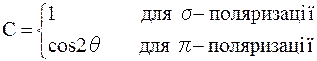, (1.21)

де s- поляризація випромінювання перпендикулярна площині дифракції, а p- поляризація паралельна їй; q- кут Брега. В цьому випадку дифракції немає принципової різниці між поляризаціями, оскільки перехід від рішення для s- поляризації вектору 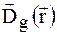до рішення для p- поляризації виконується формальною заміною в системі (1.20): .

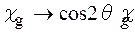Згідно елементарної кінематичної теорії дифракції вектор 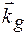за величиною і напрямком визначається умовою (1.16), із якої трикутник із векторів 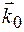, 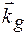і 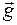є рівнобедрений і кут між векторами 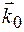і 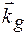рівний подвоєному куту q (рис.1). Умова (1.16) є ідеалізованою, оскільки вона визначає лише величину і напрямок хвильового вектору дифракційної хвилі 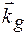без врахування ефектів заломлення і взаємодії хвиль в кристалі і точно в максимумі кривої дифракційного відбивання. Тобто умова (1.16) одночасно представляє собою і умову фазового синхроїзму – умову найбільш ефективної конструктивної інтерференції розсіяних хвиль, і закон збереження квазіімпульсу для поля в кристалі.

Реально кристал відбиває випромінювання в деякому кінечному інтервалі кутів навколо цього напрямку. Це значить, що при незначній зміні напрямку падіння первинного променю дифракційний промінь не зразу пропадає, а лише поступово по мірі віддалення від точного кута Брега q. Дослідимо, як при цьому зміниться умова (1.16). Трикутник дифракції повинен залишатись замкнутим, оскільки ця умова представляє собою закон збереження квазіімпульсу поля в кристалі. Для цього, очевидно, кристал повинен володіти дуже сильною просторовою дисперсією у вузькому кутовому інтервалі поблизу кута q₀. Дійсно, положення вектора дифракції 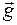фіксовано у просторі, оскільки визначається орієнтацією відбивної системи площин. Тому при зміні напрямку хвильового вектору 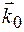(напрямок падіння первинної хвилі) хвильовий вектор 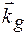повинен не тільки змінити своє положення в просторі, але і в кристалі. Щоб встановити, як міняється величина вектора 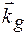при повороті 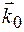, розглянемо рис.3. Із теореми косинусів для DА¢ ОВ¢ маємо 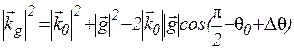, де Dq– кут повороту вектору 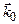, що відраховується від кута q₀, а 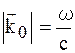. Величина Dq– додатна, якщо кут падіння променю більше q₀.

Поставимо 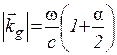, де в силу малості Dq добавка до величини хвильового вектору a/2 набагато менше 1 (a/2< < 1). Величина a і визначає необхідну для виконання закону збереження квазіімпульсу зміни фазової швидкості вторинних хвиль, що розповсюджуються під кутом падіння q, відмінним від кута q₀, для якого виконується умова фазового синхроїзму (1.16). Використовуючи введені позначення і зберігаючи тільки лінійні по a складові, знаходимо

_.

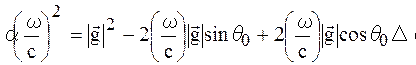Дві перших складові в правій частині, згідно умови дифракції (1.16), взаємно знищуються. Повторно використовуючи цю умову у вигляді умови Вульфа-Брега (1.16а), отримаємо

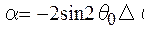, (1.22)

де 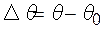, так що

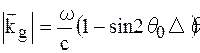. (1.23)

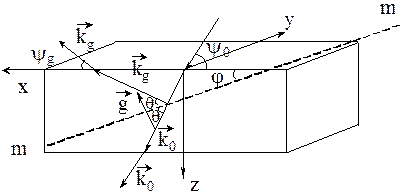
Рис.2. Система координат і одна з можливих схем двохвильової дифракції – асиметричне брегівське відбивання; 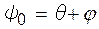і 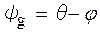- кути ковзання і виходу падаючої і відбитої хвиль відповідно; t- товщина кристалу; 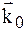- хвильовий вектор падаючої на кристал хвилі; j- кут між системою відбивних площин і вхідною поверхнею кристалу.

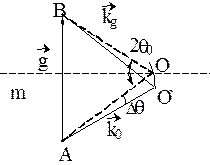
Рис.3. Визначення величини акомодації a (1.22). Умова дифракції при відхиленні кута падіння q первинної хвилі від точного кута Брега q₀ на кут Dq< 0. Штрих-пунктирними лініями показані хвильові вектори 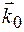і 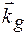в точному положенні дифракції (1.16); ОО` – дуга кола радіусу 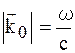, по якій переміщається початок хвильового вектора 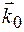при зміні напрямку розповсюдження первинної хвилі.

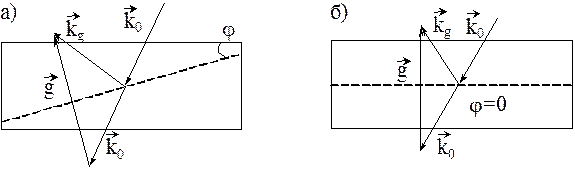
Рис.4. Схеми відбивання за Брегом: а- асиметричний випадок; б- симетричний (j=0).

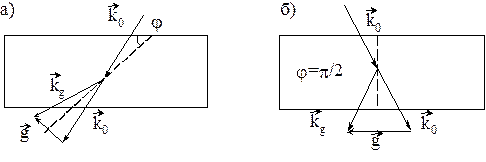
Рис.5 Схема дифракції за Лауе: а) асиметричний випадок; б) симетричний.

Рис. 6. Одна із можливих різко асиметричних схем: брегівське відбивання при 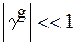. Кут падіння дифрагованого променю відносно поверхні кристалу близький до кута повного зовнішнього відбивання y_g»q_кр; 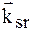- хвильовий вектор дзеркально відбитої хвилі.

Для рішення конкретних дифракційних задач слідує задати граничні умови:

для геометрії Брега: 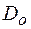=0 при z=0; 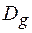=0 при z= l (1.26а)

для геометрії Лауе: 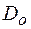=1 при z=0; 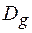=0 при z=0 (1.26б)

Граничні умови на похідні амплітуд 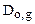отримуються підстановкою (1.26а) або (1.26б) в систему (1.25). Зазначимо, що в геометрії Брега граничні умови задаються на різних поверхнях кристалу, а в геометрії Лауе – тільки на вхідній.

Величину a назвемо акомодацією. Враховуючи (1.23) і (1.21) перепишемо систему (1.20) для двохвильової дифракції у вигляді:

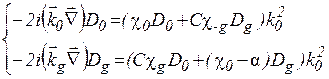(1.24)

Відзначимо, що якщо кристал однорідний по своїх властивостях вздовж вісі х, а падаюча на нього хвиля плоска, то амплітуди 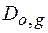не залежать від координати х і задача із двовимірної стає одновимірною. При цьому система диференціальних рівнянь в частинних похідних (1.24) переходить в систему звичайних диференціальних рівнянь з постійними коефіцієнтами:

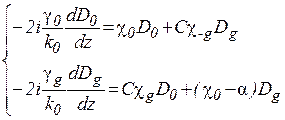(1.25)

де 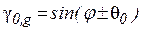– направляючі косинуси хвильових векторів .

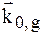В лівій частині (1.25) другого рівняння опущений малий член, пропорційний 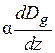. Крім того, в 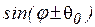під q ми приймаємо не врахованим заломлення, тобто кут q₀. Іншими словами, кут q в цих виразах змінний, проте врахування цього факту дає в системі (1.25) складові другого порядку малості, які в рамках зроблених вище наближень також можна опустити.

Отже, отримана нами система (1.25) описує розповсюдження в кристалі двох зв’язаних хвиль з амплітудами 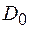і 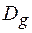на довільній глибині z під вхідною поверхнею пластини в залежності від величини акомодації a (тобто згідно (1.22), від величини кутового відхилення Dq). Члени пропорційні в рівняннях системи (1.25) описують явища заломлення 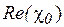і фотоелектричне поглинання 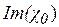хвиль. Складова пропорційна 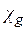, описує процес розсіяння поля із заломленої хвилі в дифраговану і навпаки, а складова пропорційна a– просторову дисперсію хвильових векторів 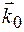і 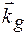при відхиленні напрямку розповсюдження падаючої на кристал хвилі від напрямку, що визначається умовою Вульфа - Брега (1.16а). Власне всі динамічні ефекти взаємодії хвиль в кристалі описуються складовою, пропорційною 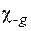, оскільки саме вона враховує існування оберненого зв’язку між хвилями 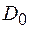і .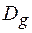

Для двопроменевої дифракції розрізняють наступні геометрії дифракції: а) падаюча і дифрагована хвилі лежать по одну сторону пластини – геометрія Брега (рис.4) 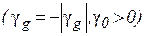; б) падаюча і дифрагована хвилі лежать по різні сторони пластини – геометрія Лауе (рис.5) .

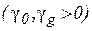Часткові випадки при j=0 і j=p/2 називаються, відповідно, симетричними геометріями Брега і Лауе. В першому випадку вектор 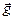перпендикулярний поверхні пластини, а в другому – паралельний їй (рис.4б і рис.5б). Всі інші геометрії асиметричні. Природно, що між геометріями Брега і Лауе повинна існувати проміжна область, коли дифрагований промінь розповсюджується вздовж кристалічної пластини в інтервалі кутів Dq~2q_кр, де 2q_кр– критичний кут повного зовнішнього відбивання рентгенівських променів. При такій умові дифрагований промінь повністю або частково розповсюджується в середині кристалу. В цій області кутів, в якій наряду з дифракцією суттєво проявляється повне зовнішнє відбивання, система рівнянь (1.25) непридатна, так як 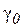або 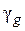є значно меншими одиниці і вже не можна знехтувати другими похідними п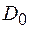о або 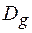в системі рівнянь (1.17). Такі геометрії називаються різко асиметричними.

Рішення системи (1.25) для полів 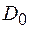і 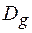записують не через кутове відхилення Dq, а через зміну у, яка наступним чином пов’язана з акомодацією a:

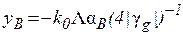для геометрії Брега (1.27а)

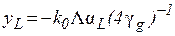для геометрії Лауе (1.27б).

Тут 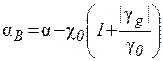, 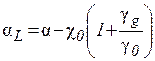– брегівська і лауевська акомодації, відповідно, що враховують ефекти заломлення хвиль в кристалі,

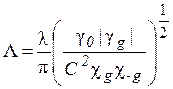(1.27в)

Якщо вважати, що кристал має нехтовно мале поглинання, то L рівна довжині первинної екстинкції 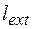. В противному випадку довжина первинної екстинкції 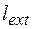визначається як дійсна частина L:

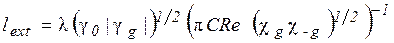
Величина у_В, а також і у_L при дуже незначному поглинанні мають зміст нормованого кутового відхилення кутової від невиправленого на заломлення кута Брега q₀, вираженої в одиницях ширини області повного відбивання:

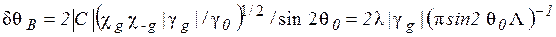
для ідеального кристалу напівбезмежної товщини. Згідно (1.22) і (1.27а) нормована зміна у_В (і у_L) має той же знак, що і кутове відхилення Dq: при збільшенні кута падіння первинного пучка Dq> 0 і у_В> 0.