
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Форми зображення логічних функцій.
|
|
Будь-яку логічну функцію можна задати або зобразити у різних формах: словесне, таблично, числового запису, аналітичне і координатної карти чи діаграми. Розглдаємо кожну з цих форм окремо. Словесне зображення – це логічне висловлення, під яким розуміють довільне твердження, щодо якого можна сказати, істинне воно або хибне.
Словесне зображення – це логічне висловлення, під яким розуміють довільне твердження, щодо якого можна сказати, істинне воно або хибне. Наприклад, функцію  – імплікацію від
– імплікацію від 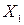 до
до 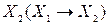 словесно можна зобразити (описати) так: функція
словесно можна зобразити (описати) так: функція 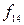 хибна тоді і тільки тоді, коли
хибна тоді і тільки тоді, коли 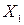 істинне і
істинне і  хибне.
хибне.
Табличне зображення характеризується таблицею істинності, яка має  рядки за числом вхідних наборів, n-стовпців за числом змінних
рядки за числом вхідних наборів, n-стовпців за числом змінних  і m-стовпців за числом функцій (
і m-стовпців за числом функцій ( ). У випадку однозначної функції число стовпців таблиці істинності дорівнює
). У випадку однозначної функції число стовпців таблиці істинності дорівнює 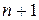 , а для багатозначної функції
, а для багатозначної функції 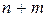 . Приклад однозначної функції трьох змінних
. Приклад однозначної функції трьох змінних 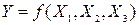 , яку зображено таблицею істинності, наведеної у табл.6. Функцію, зображену таблицею істинності, можна також “читати” аналогічно, як при словесному зображенні.
, яку зображено таблицею істинності, наведеної у табл.6. Функцію, зображену таблицею істинності, можна також “читати” аналогічно, як при словесному зображенні.
Кожний спосіб чи форма зображення має свою специфіку і тому буде зручною там, де даний спосіб є найбільш простим чи компактним.
Таблична форма запису хоча й наочна і може бути застосована для довільного числа змінних, однак при аналізі властивостей функції такий запис не є компактним. Для випадку чотирьох і більше змінних табличне зображення логічної функції є суттєво складнішим та громіздким. Простішим буде числовий запис, коли логічна функція задається у вигляді послідовності десяткових чисел, що є еквівалентами тих вхідних наборів, на яких дана функція набував значення 1 або 0.
Таблиця 6
| № | 
| 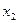
| 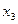
| 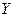
|
При аналітичному зображенні функція задається алгебраїчним виразом, який отримують при застосуванні логічних операцій до змінних бульової алгебри. Якщо попередні форми зображення логічної функції лише вказують значення функції на конкретних наборах змінних, то аналітичне зображення, крім того, ще дозволяв виконувати різні аналітичні перетворення, які необхідні як для аналізу, так і для синтезу цифрового пристрою, що реалізує або мав реалізувати дану логічну функцію.
Нехай на фіксованому вхідному наборі {  } задана логічна функція
} задана логічна функція 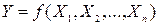 . Оскільки кожна змінна
. Оскільки кожна змінна 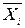 є {
є { 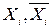 }={1, 0}, набір значень змінних, очевидно, є конкретним двійковим числом {
}={1, 0}, набір значень змінних, очевидно, є конкретним двійковим числом { 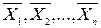 } За номер вхідного набору можна взяти довільне число
} За номер вхідного набору можна взяти довільне число
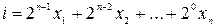
В інших випадках, наприклад, коли набір { 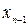 ,
, 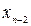 , …,
, …, 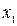 ,
, 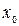 } зображує двійкове число, більш зручним є запис номера набору як
} зображує двійкове число, більш зручним є запис номера набору як

Найбільш раціональним є зображення логічних функцій в так званих нормальних (канонічних) формах запису, зокрема, у вигляді диз’юнкції кон’юнкцій або кон’юнкції диз’юнкцій змінних, що взяті з інверсіями або без них. Окремі вирази функції змінних 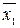 ,
, 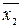 , …,
, …, 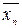 називають термами *, а самі (однозначні) функції
називають термами *, а самі (однозначні) функції 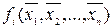 – конституентами.
– конституентами.
* Терм (від англ. term – вираз, член) – поняття алгебри логіки, що аналогічне поняттю іменника у граматиці.
Кон’юнктивний терм (мінтерм або конституента одиниці)  – це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком кон’юнкції, причому
– це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком кон’юнкції, причому
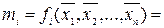
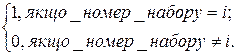
Наприклад, 
або 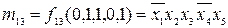
Диз’юнктивний терм (макстерм або конституента нуля) 
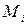 – це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком диз’юнкції, причому
– це терм, що зв’язує всі змінні, які зображені у прямій або у інверсній формі знаком диз’юнкції, причому

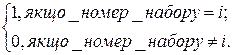
Наприклад, 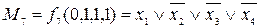
або 
Ранг терма 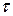 визначається кількістю змінних, які входять у даний терм. Наприклад, мінтерм
визначається кількістю змінних, які входять у даний терм. Наприклад, мінтерм  має
має 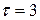 , а
, а 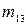 має
має  , макстерм
, макстерм 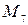 має
має 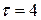 , а
, а 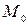 має
має 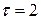 .
.
Згідно із законом дуальності будь-яку логічну функцію n-змінних можна зобразити як диз’юнкцію кон’юнкцій (мінтерм) або як кон’юнкцію диз’юнкцій (макстерм) змінних. Однозначне зображення логічних функцій одержують тільки при так-званих удосконалених нормальних формах (УНФ), тобто таких, при яких мінтерми або макстерми формуються з усіх аргументів логічної функції і в одного (причому максимального) рангу. Якщо логічна функція складається з набору диз’юнкцій елементарних кон’юнкцій одного рангу, її називають удосконаленою диз’юнктивно нормальною формою (УДНФ), а якщо– з набору кон’юнкцій елементарних диз’юнкцій – удосконаленою кон’юнктивно нормальною формою (УКНФ) зображення. Для n-змінних складається  мінітерм
мінітерм 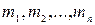 (при УДНФ) або
(при УДНФ) або  макстерм
макстерм 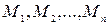 (при УКНФ2).
(при УКНФ2).
В загальному випадку алгебраїчний вираз логічної функції в УДНФ набуває вигляду
 , (1.8)
, (1.8)
де 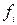 ,
, 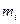 – значення функції (0 або 1) та мінтерма на i-му наборі змінних.
– значення функції (0 або 1) та мінтерма на i-му наборі змінних.
В УКНФ загальний вираз логічної функції
 , (1.9)
, (1.9)
де 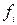 ,
,  – значення функції (0 або 1) та макстерма на i-му наборі змінних.
– значення функції (0 або 1) та макстерма на i-му наборі змінних.
Застосовуючи закони алгебри логіки (див. табл.3), неважко довести еквівалентність обох форм зображення будь-якої логічної функції. Такі форми зображення логічних функцій необхідні при проектуванні цифрових пристроїв.
Для згаданого прикладу (див. табл.6) можна записати два тотожних (дуальних) вирази логічної функції. Беручи лише до уваги конституенти 1, маємо
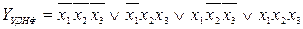 ,
,
а для конституент 0
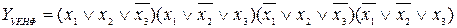 .
.
Отже, якщо логічну функцію задано таблично, то для переходу до її аналітичного зображення в УНФ роблять так:
для зображення в УДНФ виписують ті набори змінних, для яких функція дорівнює одиниці, тобто для конституент 1; для кожного такого набору складають мінтерм, причому змінні 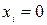 замінюють на
замінюють на 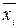 і одержані мінтерми з’єднують диз’юнкцією;
і одержані мінтерми з’єднують диз’юнкцією;
для зображення в УКНФ виписують набори, для яких функція дорівнює нулю, тобто для конституент 1; для кожного набору складають макстерм, причому змінні 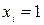 замінюють на
замінюють на 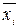 і одержані макстерми об’єднують кон’юнкцією.
і одержані макстерми об’єднують кон’юнкцією.
Слід зауважити, що в даному прикладі вибір форми зображення логічної функції не має принципового значення, бо число мінтерм дорівнюз числу макстерм. Проте у випадках, коли число одних переважав над числом інших, наприклад, кількість 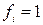 більша за кількість
більша за кількість 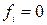 , або навпаки, тоді менш громіздким буде функція з меншим числом терм.
, або навпаки, тоді менш громіздким буде функція з меншим числом терм.
Досить зручним і наглядним зображенням логічної функції є координатний спосіб, тобто у вигляді координатної карти (таблиці, діаграми) логічних станів. Одною з координатних форм зображення логічної функції, що знайшла найбільше поширення в інженерній практиці для досить незначного числа змінних 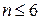 , є побудова карт мінтермів або карт Карно. Карта Карно містить
, є побудова карт мінтермів або карт Карно. Карта Карно містить  клітинок, причому кожній клітинці відповідає один з
клітинок, причому кожній клітинці відповідає один з  мінтермів. Для логічної функції, яка задана в УДНФ, в клітинках карти записуються 1 відповідних мінтерм, для яких функція дорівнює одиниці. Значення функції, що дорівнюз нулю в карті, як правило, не відображається.
мінтермів. Для логічної функції, яка задана в УДНФ, в клітинках карти записуються 1 відповідних мінтерм, для яких функція дорівнює одиниці. Значення функції, що дорівнюз нулю в карті, як правило, не відображається.
Карта Карно будується так, щоб сусідні клітинки відрізнялися значенням тільки одної змінної. Сусідніми вважаються ті клітинки карти Карно, які дотикаються своїми сторонами, а також клітинки, що розташовані по краях карти (у верхньому і нижньому рядках та лівому і правому стовпцях).
На рис.1.2, а-в, показані таблиці Карно для логічних функцій відповідно двох, трьох і чотирьох змінних.
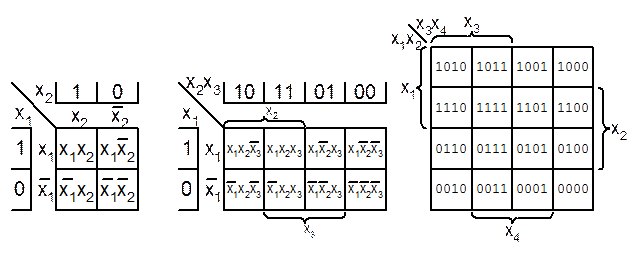
а) б) в)
Рис. 1.2. Таблиці Карно.
Таблицю Карно для п’яти і більше змінних розглядають як складену з меншого числа змінних, тобто з двох або біпьше простих підкарт. Наприклад, карту для п’яти змінних будують як дві підкарти для чотирьох змінних. При цьому зручно під’єднати (склеїти) їх одну до одної зі сторони одно іменних стовпців. Сусідніми клітинками тоді будуть також клітинки стовпців, що симетрично розташовані відносно лінії з’єднання підкарт для чотирьох змінних одноіменних рядків.
Для логічних функцій з числом змінних 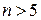 карти Карно стають громіздкими, адже число клітинок для
карти Карно стають громіздкими, адже число клітинок для  становить
становить 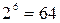 , що стає незручним для практичного застосування.
, що стає незручним для практичного застосування.
Зведення логічної функції до УНДФ або до УКНФ дає однозначне зображення  . Однак для технічної реалізації такої логічної функції властивість однозначності зображення буде зручним тільки в тому випадку, якщо повним набором логічних елементів з елементарний базис, що складається з окремих елементів I, АБО, НЕ, причому з числом входів елементів І та АБО, що дорівнює рангу термів логічної функції. На практиці часто доводиться будувати цифрові пристрої на різних базисах, і тоді з’ясовується, що удосконалені форми зображення логічних функцій не завжди найекономніші. Їм властива надлишковість, яка підлягав спрощенню, тобто мінімізації. Цій процедурі, до речі, можуть підлягати логічні функції інших, не обов’язково удосконалених, форм зображення.
. Однак для технічної реалізації такої логічної функції властивість однозначності зображення буде зручним тільки в тому випадку, якщо повним набором логічних елементів з елементарний базис, що складається з окремих елементів I, АБО, НЕ, причому з числом входів елементів І та АБО, що дорівнює рангу термів логічної функції. На практиці часто доводиться будувати цифрові пристрої на різних базисах, і тоді з’ясовується, що удосконалені форми зображення логічних функцій не завжди найекономніші. Їм властива надлишковість, яка підлягав спрощенню, тобто мінімізації. Цій процедурі, до речі, можуть підлягати логічні функції інших, не обов’язково удосконалених, форм зображення.
Мінімізація – це процес зведення логічної функції до такого виду, який припускає більш просту і дешеву її фізичну реалізацію, тобто з меншим числом логічних елементів за рахунок зменшення числа логічних символів, кількості змінних та зв’язків між елементами.
Відомо кілька методів мінімізації [2-4], серед яких найбільш поширеними в інженерній практиці є такі:
· безпосередніх перетворень;
· карт Карно;
· Квайна.
Знайти гарантовано мінімальний вираз для довільної логічної функції можна лише методом повного перебору в процесі мінімізації всіх можливих варіантів. Від руки (на папері) це реально здійснити для невеликої кількості змінних. Із збільшенням числа змінних складність розглянутих методів мінімізації зростає за геометричною прогресією і стає під силу лише автоматизованим методам, які призначені для ЕОМ.
Розглянемо перераховані методи мінімізації логічних функцій.
Метод безпосередніх перетворень – це аналітичний метод спрощення логічних функцій з допомогою аксіом та законів бульової алгебри. При набутті певних навичок цей метод є досить ефективним для малої кількості змінних (як правило, не більше трьох).
Для мінімізації логічних функцій методом безпосередніх перетворень корисно використовувати такі формули бульової алгебри:

| 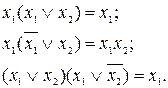 (1.10) (1.10)
|
У деяких випадках ефективніше мінімізувати інверсію логічної функції для отримання простішого виразу в МДНФ. Це може бути тоді, коли логічна функція має переважаюче число одиниць, ніж кулів. Тоді, маючи МДНФ інверсної функції, при технічній реалізації цієї функції достатньо на виході побудованої схеми під’єднати інвертор для відновлення прямої функції.
Метод таблиць (карт) Карно застосовують переважно для мінімізації логічних функцій невеликого числа змінних (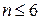 ). Необхідного умовою застосування цього методу є попереднє зображення заданої логічної функції в УДНФ. Якщо метод безпосередніх перетворень є універсальним, причому кінцевий результат залежить від кваліфікації користувача, даний метод відрізняється простотою та наглядністю, а при дотриманні формальних правил– іноді простішим кінцевим виразом МДНФ.
). Необхідного умовою застосування цього методу є попереднє зображення заданої логічної функції в УДНФ. Якщо метод безпосередніх перетворень є універсальним, причому кінцевий результат залежить від кваліфікації користувача, даний метод відрізняється простотою та наглядністю, а при дотриманні формальних правил– іноді простішим кінцевим виразом МДНФ.
Суть мінімізації за допомогою карт Карно полягає в тому, що шукаються мінтерми (конституенти 1), які “склеюються” за законом склеювання для диз’юнкції. Склеєними вважаються сусідні одиниці, які розташовані як у вертикальних, так і у горизонтальних клітинках. Сусідніми вважаються також клітинки, які стають суміжними після згортання карти у горизонтальний і у вертикальний циліндр. Це бував тільки для випадку логічних функцій, що мають три або більше змінних. Оскільки дві сусідні клітинки карти Карно відрізняються лише на одну зміну, диз’юнкція цих двох мінтермів дає один кон’юнктивний член, з якого вилучена спільна змінна (згідно із законом склеювання для диз’юнкцїй). У карті Карно клітинки з одиницями графічно об’єднують обведенням контурів, що відповідає процедурі покриття. Це еквівалентно. виділенню спрощеного мінтерма, а саме – доповнення типу (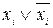 ). Всі об’єднані (по 2, 4 або по 8) клітинки відповідають мінтермам-імплікантам, диз’юнкція яких дає МДНФ даної логічної функції.
). Всі об’єднані (по 2, 4 або по 8) клітинки відповідають мінтермам-імплікантам, диз’юнкція яких дає МДНФ даної логічної функції.
Зауважимо, що будувати карту Карно для логічної функції двох змінних недоцільно. В цьому випадку простіше функцію мінімізувати аналітичним методом.
Таким чином, процес мінімізації за допомогою каpт Карно зводиться до знаходження найбільших за площею покриттів з  сусідніх (заповнених) клітинок. Чим більше клітинок карти Карно в покритті, тим простіша імпліканта. При цьому слід прагнути до того, щоб кожна заповнена клітинка обов’язково входила в яке-небудь покриття. Імпліканта, що відповідає деякому покриттю заповнених клітинок карти, містить символи тих змінних, значення яких збігаються у всіх об’єднаних клітинках.
сусідніх (заповнених) клітинок. Чим більше клітинок карти Карно в покритті, тим простіша імпліканта. При цьому слід прагнути до того, щоб кожна заповнена клітинка обов’язково входила в яке-небудь покриття. Імпліканта, що відповідає деякому покриттю заповнених клітинок карти, містить символи тих змінних, значення яких збігаються у всіх об’єднаних клітинках.
Проілюструємо процес мінімізації методом карт Карно на прикладі для логічної функції:
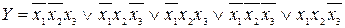 .
.
Спочатку задану функцію зобразимо картою Карно, розміщуючи у відповідні клітинки конституенти 1 (рис.1.3). Далі об’єднуємо конституенти сусідніх клітинок (тобто виконуємо покриття), у даному випадку по дві одиниці (контур 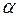 ) і по чотири одиниці (контур
) і по чотири одиниці (контур 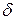 ). Тепер можна виконати так зване зчитування карти, тобто одержати з об’єднаних клітинок імпліканти. Такими імплікантами в даному випадку для контуру
). Тепер можна виконати так зване зчитування карти, тобто одержати з об’єднаних клітинок імпліканти. Такими імплікантами в даному випадку для контуру 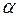 є
є  і для контуру
і для контуру 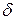 –
– 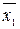 , які для одержання результату МДНФ об’єднують диз’юнкцією, а саме:
, які для одержання результату МДНФ об’єднують диз’юнкцією, а саме: 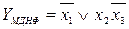 .
.
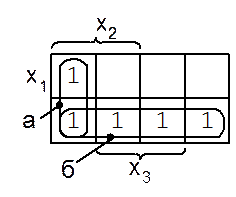
Рис. 1.3. Метод склеювання клітинок таблиць Карно.
|
|