
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модулярна арифметика.
|
|
Основною в модулярній арифметиці вважається алгебраїчна операція знаходження остачі r від ділення цілого числа a на натуральне число m, що позначається як r = a mod m.
Ця операція здійснюється на підставі наступного правила.
Правило 1.1. Будь-яке ціле a подається через натуральне m единим способом a = m × q + r, де ціле q називається неповною часткою, m називається модулем, 0 ≤ r < m називається остачею від ділення або залишком числа a по модулю m.
Операція знаходження неповної частки q від ділення цілого числа a на натуральне число m позначається як q = a div m.
Приклад 1. Знайдемо q і r для чисел a = 43 і m = 11. Виконаємо звичайне ділення:
a/m=43/11 =3.9091
Заокруглимо отриманий десятковий дріб до цілого в меншу сторону:
отримаємо q = 3. Тепер за формулою r = a - m × q знайдемо: r = 43 - 11 × 3 = 10.
Означення 1.1. Якщо двум цілим a і b відповідає одна й та ж остача r, то вони називаються конгруентними по модулю m, тобто a ≡ b (mod m).
Приклад 3. Відомо, що r = 17 mod 5 = 2 і r = 32mod 5 = 2. Отже, можна записати, що 32 ≡ 17 (mod 5).
Найбільший спільний дільник.
Означення 2.1. Найбільший спільний дільник натуральних чисел M і N позначається НСД(M, N) і являє собою найбільше можливе натуральне число, на яке ці числа діляться без остачі.
Означення 2.2. Натуральні числа M і N, для яких НСД(M, N)=1, називаються взаємно простими.
В кріптографії досить часто використовуються взаємно прості числа, тому потрібний алгоритм пошуку НСД для перевірки, чи не є дані числа взаємно простими.
Пошук Найбільшого Спільного Дільника базується на алгоритмі Евкліда.
Розглянемо деякі додатні цілі M і N, для яких M > N. Тоді число M можна єдиним способом представити у вигляді M = N * q + r, де 0 < r < N. Тут ціле число q – неповна частка, а r – остача від ділення M на N. В окремому випадку, якщо r = 0, то кажуть, що M кратно N, або, що M ділиться на N без остачі
Наприклад, при M = 140 і N = 12 маємо 140 = 12 * 11 + 8. Тепер розглянемо дільників чисел M і N: число M = 140 має 12 дільників (1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70 і 140), число N = 12 має 6 дільників (1, 2, 3, 4, 6 і 12). Бачимо, що серед дільників чисел M і N є спільні (1, 2 і 4). Найбільший серед них – це 4.
Правило 2.1. Якщо для даних додатних цілих M > N виконується рівність M = N * q + r, де q – ціле, 0 < r < N, то сукупність спільних дільників чисел M і N співпадає із сукупністю спільних дільників чисел N і r. Зокрема, найбільший спільний дільник чисел M і N рівний найбільшому спільному дільнику чисел N і r.
Замінимо дані числа M і N числами N і r відповідно. Нові числа M і N представимо аналогічно і т.д. Цей процес закінчується, коли отримуємо деяку остачу від ділення r = 0.
Якщо остання остача від ділення у цьому процесі обов’язково дорівнює нулю, то це означає, що в останній парі M кратно N, тобто N є дільником числа M. Отже, остання не рівна нулю остача одночасно є найбільшим спільним дільником у процесі утворення всіх послідовних пар чисел M і N, в тому числі і для даної початкової пари M і N.
Деякі поняття матричної алгебри
Означення 3.1. У загальному випадку добутком матриці A = (aij) розміром m*k на
матрицю B = (bij) розміром k*n називається матриця C = (cij) розміром m*n, в якій кожний
елемент cij дорівнює сумі добутків елементів i-го рядка матриці A та j-го стовпчика матриці
B, тобто для всіх i та j справедлива рівність  .
.
Добуток матриць C=A× B існує тільки тоді, коли кількість стовпчиків матриці A
дорівнює кількості рядків матриці B. При цьому результат множення C має ту ж кількість
рядків, що й матриця A, і ту ж кількість стовпчиків, що й матриця B.
Якщо в матриці кількості рядків та стовпчиків співпадають, тобто m=n, то матриця
називається квадратною. Кількість рядків або стовпчиків квадратної матриці називається її
порядком. Для квадратної матриці C порядку n існує поняття оберненої матриці.
Означення 3.2. Оберненою матрицею C-1 порядку n називається така матриця, яка
задовольняє умові C - 1 × C = C × C - 1 = E, де E – одинична матриця порядку n, тобто така
діагональна матриця, всі елементи головної діагоналі якої рівні одиниці.
Правило 3.1. Обернена матриця обчислюється за формулою

, де D – визначник матриці C, Cij – алгебраїчні доповнення
елементів cij, які обчислюються через відповідні мінори.
Мінором елемента ij c у даному визначнику порядка n називається інший визначник
порядка n-1, який утворюється, якщо із даного визначника викреслити рядок і стовпчик, на
перетині яких стоїть елемент ij c. Мінор елемента ij c позначається ij M.
Алгебраїчним доповненням деякого елемента ij c у даному визначнику називається
мінор цього елемента, помножений на величину (- 1) i j, тобто Cij = (- 1) i j × M i j.
Прості числа. Означення простого числа. Тестування числа на простоту.
Кріптографія використовує дуже великі прості числа. На жаль, використання стандартних засобів мов програмування надає можливість працювати лише з такими цілими числами, значення яких не виходять за межі довгого цілого типу LongInt, для якого
найбільше допустиме значення становить 2147483647 що далеко не задовольняє потреби кріптографії. Саме тому дуже важливо розробляти швидкодіючі алгоритми обробки простих чисел.
Теорія чисел визначає прості числа наступним чином:
· всі натуральні числа, крім 1, мають, щонайменше, двох дільників – одиницю та самого себе;
· ті з них, що не мають ніяких інших дільників, називаються простими; наприклад, декілька перших простих чисел 2, 3, 5, 7, 11, 13, 17, 19;
· ті числа, які мають ще й інших дільників, називаються складеними; наприклад, 12 – складене число (його дільники 1, 2, 3, 4, 6, 12);
· число 1 розглядають окремо, не відносячи ні до простих, ні до складених, оскільки одиниця не має всіх властивостей, справедливих для всіх інших простих чисел.
Тестуванням деякого числа M числа на простоту називається перевірка, є дане число M простим чи ні. Для цього достатньо перевірити всі можливі прості дільники цього числа за винятком самого числа M.
Якщо остача від ділення числа M на деякий можливий простий його дільник рівна
нулю, то таке число M не є простим.
Всі можливі прості дільники числа M, яких слід перевірити, знаходяться в межах від 2 до M div 2. Для великого числа M така перевірка може тривати занадто довго. Тому важливе значення мають різні методи скорочення терміну перевірки.
Один із методів пов’язаний з тим, що дільники числа завжди зустрічаються парами. Наприклад, число 144 має своїм дільником число 3, тобто 144 mod 3 = 0. Але дільник 3 обов’язково супроводжується також дільником 48, оскільки 48 * 3 = 144. Таким чином, зрозуміло, що перевіривши дільник 3, немає потреби перевіряти супутній дільник 48. Остаточний висновок за таких умов полягає в тому, що при тестуванні числа M на простоту достатньо перевірити тих можливих простих дільників, які знаходяться в межах від 2 до √ M.
Набори залишків та первісні корені.
Означення 5.1. Набір m цілих чисел від 0 до m-1 називається повним набором
залишків по модулю m.
Це означає, що для будь-якого r в межах від 0 до m-1 завжди знайдеться ціле число a, для якого задовольняється співвідношення r = a – m · q, де q – ціле число.
Наприклад, повний набір залишків для m=12 становить r Î { 0, 1, 2, K, 11 }. При цьому для r = 7 справедлива рівність 7 = 31 – 12 · 2, де a = 31, для r = 2 – рівність 2 = 14 – 12 · 1, де a = 14 і т.д.
Означення 5.4. Дано просте число p. Ціле число g називається первісним коренем за простим модулем p, якщо послідовність, яка складається із p–1 елементів
g0mod p = 1, g1mod p, g2mod p, g3mod p,..., g p - 2 mod p містить всі елементи зведеного набору залишків по модулю p, тобто { 1, 2,...., p - 1 }.
Дискретне піднесення до степеня.
Реальний процес дискретного піднесення до степеня 750 mod 11 можна представити у
вигляді наступної таблиці:


Зміст таблиці циклічного процесу дискретного піднесення до степеня наступний:
· стовпчик Показник містить результати поступового цілочисельного ділення на 2 даного показника степеня 50; ознакою завершення процесу є нульове значення показника степеня;
· в стовпчику Основа здійснюється множення попереднього результату самого на себе за заданим модулем, починаючи із заданого значення 7;
· в стовпчику Результат здійснюється накопичення потрібного результату шляхом множення попереднього його значення на поточне значення Основи в ті моменти, коли Показник є непарним; початкове значення Результату вважається рівним одиниці
Особливо добре ефективність бінарного методу видно на великих числах.
Розширений алгоритм Евкліда.
Відомо, що взаємно прості числа – це такі натуральні числа a і b, для яких НСД(a, b)=1. Для кожної пари взаємно простих чисел a і b завжди можна знайти такі цілі u і v, що u × a + v × b = 1. Для розв’язування цього рівняння використовують розширений алгоритм Евкліда, основні складові якого такі:
· послідовно виконують ділення з остачею попереднього значення натурального ri-1 на наступне ri у відповідності із рівністю ri-1=ri*qi+1+ri+1;
· використовують рекурентне співвідношення ui-1=ui*qi+1+ui+1;
· використовують рекурентне співвідношення vi-1=vi*qi+1+vi+1;
· щоб почати процес виконання алгоритму, використовують значення r0=a, r1=b, u0=1, u1=0, v0=0, v1=1
Роботу алгоритма демонструє таблиця виконання для a = 211, b = 79.
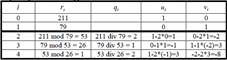
Кінець процесу при r i = 1. При цьому u = 3, v = - 8. Дійсно, 3*211+(-8)*79=633-632=1.
Функція Ейлера та мала теорема Ферма.
Функція Ейлера j(m) визначається як кількість натуральних чисел, які менші m та
взаємно прості з ним. Інакше кажучи, функція Ейлера указує число елементів зведеного
набору залишків по модулю m.
Приклад 1. Для m=10 взаємно простими з ним та меншими його є натуральні числа 1,
3, 7 і 9. Отже, ᵩ (10) = 4.
Функція Ейлера має властивість, яка називається її мультиплікативністю, а саме: для
попарно взаємно простих m1, m2… mk справедлива рівність
ᵩ (m1*m2*…mk)= ᵩ (m1)* ᵩ (m2)… ᵩ (mk)
З функцією Ейлера пов’язана його ж знаменита теорема: для взаємно простих цілого
x і натурального m справедлива конгруенція x ᵩ ( m)≡ 1(mod m) або x ᵩ ( m) mod m =1.
Наслідок з теореми Ейлера відомий під назвою “ мала теорема Ферма ”.
Якщо p – просте число і НОД(a, p) = 1, то a p - 1 ≡ 1 (mod p) або a p - 1 mod p = 1.
Мультиплікативно обернене число.
Мультиплікативно оберненим числу 0 < a < m по модулю m називається число
0< a - 1 < m таке, що a × a - 1 ≡ 1 (mod m).
Ще Евклід стверджував, що таке число існує тільки тоді,
коли a і m – взаємно прості числа. Наприклад, мультиплікативно оберненими є:
· 7 і 4 по модулю 9, оскільки (7·4) mod 9 = 28 mod 9 = 1;
· 3 і 3 по модулю 8, оскільки (3·3) mod 8 = 9 mod 8 = 1;
Китайська теорема про остачі.
Для будь-якої пари взаємно простих натуральних чисел m1 і m2 та для будь-якої пари цілих чисел x1 і x2 можна знайти таке ціле x, що x≡ x1(mod m1) i x≡ x2(mod m2).
Отже, дана теорема дозволяє відновити число, якщо відомі його залишки за деякими модулями.
Алгоритм пошуку такого x визначається рівністю 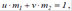 , із якої випливає,
, із якої випливає,
що  . В свою чергу, використовуючи ці рівності, можна пересвідчитись, що число
. В свою чергу, використовуючи ці рівності, можна пересвідчитись, що число  задовольняє заданим умовам, тобто
задовольняє заданим умовам, тобто  . І цим умовам задовольняє також шукане число
. І цим умовам задовольняє також шукане число
 , яке є остачею від ділення
, яке є остачею від ділення 
Цілі числа u і v, які задовольняють рівності  , можна знайти за
, можна знайти за
допомогою розширеного алгоритма Евкліда
Звужена задача факторизації.
Цілочисельне множення належить до класу односторонніх функцій. Пряма задача – обчислення добутку послідовності дуже великих чисел є відносно простою. Обернена задача називається задачею факторізації. Вона полягає у розкладі даного натурального числа n на прості множники і вважається практично нерозв’язуваною. Особливо ускладнюється розв’язок цієї задачі при невідомій кількості співмножників.
Якщо відомо, що n є добутком тільки двох простих чисел, то виникає звужена задача факторизації, розв’язок якої був запропонований Ферма.
Припустимо, що n = p × q, де p і q – досить великі прості числа. Припустимо також,
що різниця q - p невелика і, крім того, p≠ 2
За таких умов q - p – парне число, і можна записати q = p + 2× d. Тоді
 Алгоритм розв’язування полягає в тому, що послідовно переглядають числа t (відповідник p + d), які відповідають умові t 2 ≥ n, і перевіряють, чи не є t 2 - n повним квадратом. Якщо це так, то
Алгоритм розв’язування полягає в тому, що послідовно переглядають числа t (відповідник p + d), які відповідають умові t 2 ≥ n, і перевіряють, чи не є t 2 - n повним квадратом. Якщо це так, то  , звідки отримуємо
, звідки отримуємо
p = t - d, q = t + d.
5. ШИФРИ АНАЛІТИЧНИХ ПЕРЕТВОРЕНЬ.
|
|