
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Практическое занятие 2
|
|
1. Даны точки А(2; 3; -1) и В(1; -2; -1). Найти координаты вектора 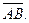
Отв. A) (-1; -5; 0); B(3; 1; -2); C(2; -6; 1); D(1; 5; 0); E(-2; 6; -1).
2. Даны векторы 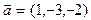 и
и 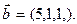 Найти вектор
Найти вектор 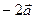 +
+ 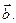
Отв. A) (6; -2; -1); B(3; 7; 5); C(2; -6; 1); D(3; 7; -5); E(-3; -7; -5).
3. Найти координаты вектора 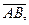 если А(1; 3; -4) и В(3; 2; 1).
если А(1; 3; -4) и В(3; 2; 1).
Отв. А) 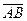 =
= 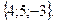 ; В)
; В) 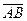 =
= 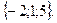 ; С)
; С) 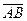 =
= 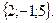 D)
D) 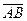 = (-2; -1; 5);
= (-2; -1; 5);
E) 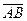 =
= 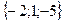 .
.
4. Найти единичный вектор вектора 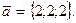
Отв. А) 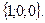 В)
В)  С)
С) 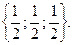 D)
D) 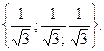 E)
E) 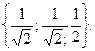
5. Найти скалярное произведение векторов 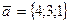 и
и 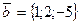 .
.
Отв. А)  ; В)
; В)  С)
С) 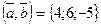 D)
D) 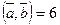 E)
E) 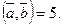
6. Указать условие перпендикулярности векторов 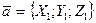 и
и 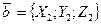 .
.
Отв. А) 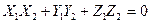 ; В)
; В) 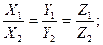 C)
C) 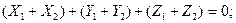
D) 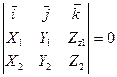 ; E)
; E)  .
.
7. Указать формулу для нахождения векторного произведения двух векторов 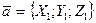 и
и 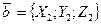 .
.
Отв. А) 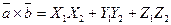 ; В)
; В) 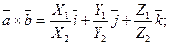
C)  ; D)
; D) 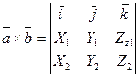 ; E)
; E) 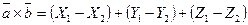 .
.
8. Найти модуль суммы векторов 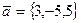 и
и 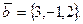
Отв. А) 3; В) 6; С) 11;.D) 9; E) 12.
9. Найти координаты вектора 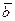 , если
, если 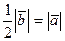 и
и 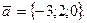 Направление вектора
Направление вектора 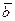 противоположно направлению вектора
противоположно направлению вектора 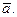
Отв. А) 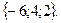 B)
B)  C)
C) 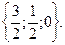 D)
D) 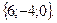 E)
E) 
10. Указать условие коллинеарности векторов 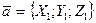 и
и 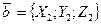 .
.
Отв. А) 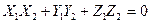 ; B)
; B) 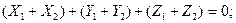
C) 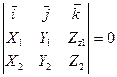 ; D)
; D)  . E)
. E) 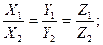
11. Найти скалярное произведение векторов 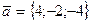 и
и 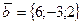 .
.
Отв.А) 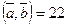 . В)
. В)  . С)
. С) 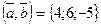 . D)
. D) 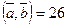 . E)
. E) 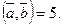
12. При каком значении k векторы 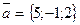 и
и 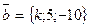 коллинеарны.
коллинеарны.
Отв. A) 25. B) –25. C) –5. D) 5. E) 2.
13. Дан модуль вектора 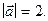 Углы, составленные вектором с осями
Углы, составленные вектором с осями
координат, равны a=450, b=600, g=1200. Вычислить проекции вектора 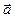 на координатные оси.
на координатные оси.
Отв. А) 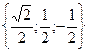 . B)
. B) 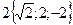 . С)
. С) 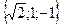 . D)
. D) 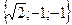 . E)
. E) 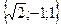 .
.
14. Вычислить направляющие косинусы вектора  .
.
Отв. A) 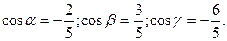 . B)
. B)  .
.
C) 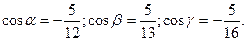 . D)
. D) 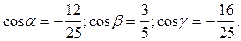 .
.
E) 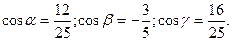 .
.
15. Найти скалярное произведение векторов 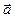 и
и 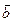 , если их модули равны 5
, если их модули равны 5
и 8 соответственно и угол между ними равен 600.
Отв. A) –20. B) 40. C) 10. D) –10. E) 20.
16.Даны векторы 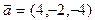 и
и 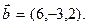 Вычислить
Вычислить 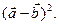
Отв. A) 41. B) 44. C) 34. D) –1. E) 3.
17. Даны векторы 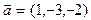 и
и 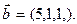 Найти координаты векторного произведения
Найти координаты векторного произведения  ,
,
Отв. A)  . B)
. B) 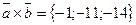 . C)
. C) 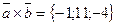 .
.
D) 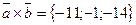 . E)
. E) 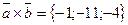 .
.
18. Даны векторы 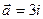 и
и 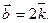 Найти координаты векторного произведения
Найти координаты векторного произведения  ,
,
Отв. A) 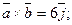 . B)
. B) 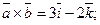 . C) D)
. C) D)  .. E)
.. E) 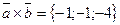 .
.
19.Вычислить площадь параллелограмма, построенного на векторах 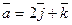 и
и 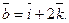
Отв. A) 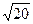 . B) 5. C) 4. D)
. B) 5. C) 4. D) 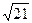 . E)
. E) 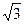 .
.
20. Найти косинус угла между векторами 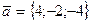 и
и 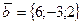 .
.
Отв. A) 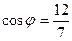 . B)
. B)  . C)
. C) 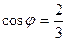 . D)
. D) 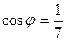 . E)
. E) 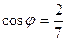 .
.
21. Найти косинус угла между векторами 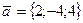 и
и 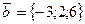 .
.
Отв. A) 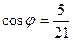 . B)
. B) 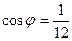 . C)
. C) 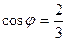 . D)
. D) 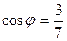 . E)
. E) 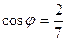 .
.
22. При каком значении m векторы 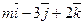 и
и 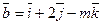 будут перпендикулярны.
будут перпендикулярны.
Отв. A)1 B) –6; C) –4; D) 4; E) 3.
23. При каком значении m векторы 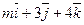 и
и  будут перпендикулярны.
будут перпендикулярны.
Отв. A)-1 B) 5; C) 4; D) -4; E) 3.
24. Найти смешанное произведение векторов 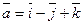 ,
,  и
и  .
.
Отв. A)1 B) –6; C) –4; D) 4; E) 3.
25. Найти объем параллелепипеда, построенного на векторах 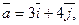
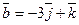 и
и 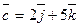 .
.
Отв. A) 41. B) 61. C) 45. D) -51. E) 51.
26. Найти объем треугольной пирамиды с вершинами в точках О (0; 0; 0), А)(5; 2; 0), В) (2; 5; 0) и С(1; 2; 4).
Отв. A) 14. B) 10. C) 12. D) 7. E) 6.
Задача 27. Даны точки 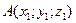 и
и 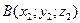 . Требуется найти:
. Требуется найти:
а) координаты векторов 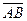 и
и 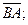
б) модуль вектора 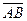 (или расстояние между точками А и В);
(или расстояние между точками А и В);
в) координаты середины отрезка АВ
| А, В. | Отв. а) | Отв. б) | Отв.в) | |
| А(5; 2; 6), В(1; 8; -2) | 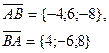
| 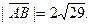
| (3; 5; 2) | |
| А(-3; 1; 0), В(7; 1; -5) | 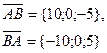
| 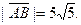
| (2; 1; 2, 5) | |
| А(2; -1; 7), В(6; 3; 4) | 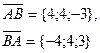
| 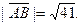
| (4; 1; 5, 5) | |
| А(2; 3; 4), В(-2; -1; 8) | 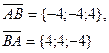
| 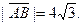
| (0; 1; 6) | |
| А(5; -4; 3), В(1; 3; -8) | 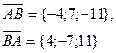
| 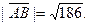
| (3; -0, 5; -2, 5) | |
| А(0; 4; 5), В(7; -2; 1) | 
| 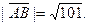
| (3, 5; 1; 3) | |
| А(2; -3; -7), В(3; 2; 8) | 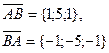
| 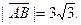
| (5, 5; -0, 5; 15, 5) | |
| А(2; 1; -6), В(1; 4; 9) | 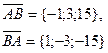
| 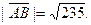
| (3, 5; 5, 5; 3, 5) | |
| А(5; 6; -3), В(7; 6; 1) | 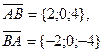
| 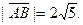
| (6; 6; -1) | |
| А(2; 8; -9), В(7; 5; -5) | 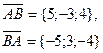
| 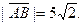
| (9, 5; 13, 5; -7) |
Задача 28. Даны векторы 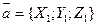 и
и  Требуется найти:
Требуется найти:
а) модуль вектора 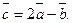 ;
;
б) направляющие косинусы вектора 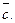
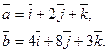
| 
| 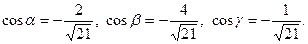
| |
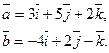
| 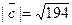
| 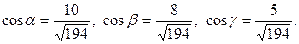
| |
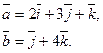
| 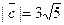
| 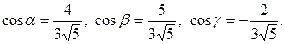
| |
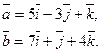
| 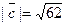
| 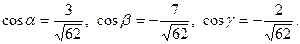
| |
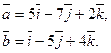
| 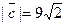
| 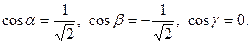
| |
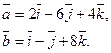
| 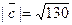
| 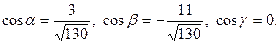
| |
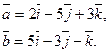
| 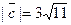
| 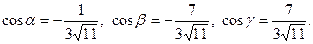
| |
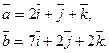
| 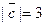
| 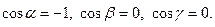
| |
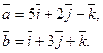
| 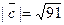
| 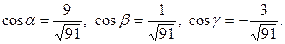
| |
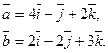
| 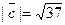
| 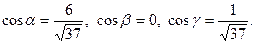
|
Задача 29. Найти скалярное произведение векторов 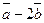 и
и 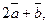 если даны модули векторов
если даны модули векторов 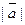 и
и  и угол j между ними.
и угол j между ними.
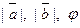
| Отв. | |
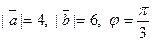
| -76 | |
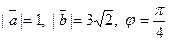
| -43 | |

| ||
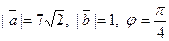
| ||

| -102 | |
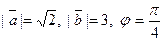
| -23 | |
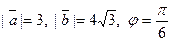
| -132 |
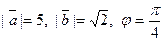
| ||
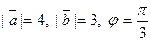
| -4 | |
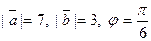
|
Задача30. Даны координаты вершин треугольника АВС. Вычислить площадь этого треугольника.

| Отв. | |
| А(1; 1; 1), B(2; 3; 4), C(4; 3; -2) |  (кв.ед) (кв.ед)
| |
| А(2; 2; 2), B(4; 0; 3), C(0; 1; 0) | 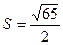 (кв.ед) (кв.ед)
| |
| А(0; 0; 1), B(2; 3; 5), C(0; 2; 3) | 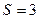 (кв.ед) (кв.ед)
| |
| А(1; 2; 0), B(3; 0; -3), C(5; 2; 6) | 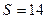 (кв.ед) (кв.ед)
| |
| А(1; -1; 2), B(5; -6; 2), C(1; 3; -1) | 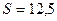 (кв.ед) (кв.ед)
| |
| А(5; -4; 3), B(1; -2; 5), C(0; 1; 2) | 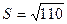 (кв.ед) (кв.ед)
| |
| А(1; -1; 3), B(4; -5; 4), C(1; 1; 4) |  (кв.ед) (кв.ед)
| |
| А(2; 5; 1), B(0; 3; -1), C(2; 5; 4) | 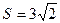 (кв.ед) (кв.ед)
| |
| А(0; 2; -1), B(5; 2; 3), C(1; 3; 2) | 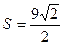 (кв.ед) (кв.ед)
| |
| А(1; 3; 1), B(0; 3; -2), C(-1; 2; 5) | 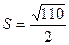 (кв.ед) (кв.ед)
|
Задача 31. Вычислить объем V параллелепипеда, построенного на векторах 

| Отв.V(куб.ед) | |
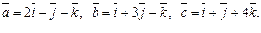
| V=33 (куб.ед.) | |
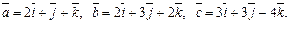
| V=7 (куб.ед.) | |
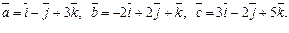
| V=7 (куб ед.) | |
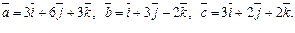
| V=18 (куб.ед.) | |
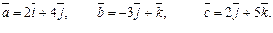
| V=51 (куб.ед.) | |
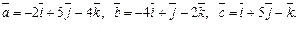
| V=36 (куб.ед.) | |
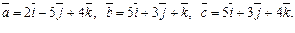
| V=93 (куб.ед.) | |
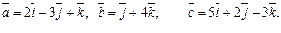
| V=87 (куб.ед.) | |
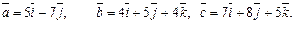
| V=91 (куб.ед.) | |

| V=54 (куб.ед.) |
Задача 32. Даны координаты вершин треугольной пирамиды А1{x1; y1; z1}, A2{x2; y2; z2}, A3{x3; y3; z3}, A4{x4; y4; z4}. Методами векторной алгебры найти:
а) длину ребра А1А2;
б) угол между ребрами А2А3 и А3А4;
в) проекцию ребра А1А3 на ребро А1А2;
г) площадь грани А1А2А3;
д) объем пирамиды А1А2А3А4.
01. А1(1; -2; 0), А2(2; 1; -2), А3(-1; -1; 3), А4(2; 3; 1).
02. А1(2; -1; 1). А2 (3; 2; -1). А3 (0; 0; 4), А4 (3; 4; 2).
03 А1(3; 0; 2). А2 (4; 3; 0). А3 (1; 1; 5), А4 (4; 5; 3).
04. А1(1; -1; 0). А2 (2; 2; -2). А3 (-1; 0; 3), А4 (2; 4; 1).
05. А1(2; -2; 0). А2 (3; 1; -2). А3 (0; -1; 3), А4 (3; 3; 1).
06. А1(1; -2; 1). А2 (2; 1; -1). А3 (-1; -1; 3), А4 (2; 3; 2).
07. А1(1; -2; 1). А2 (2; 1; -1). А3 (-1; -1; 4), А4 (2; 3; 2).
08. А1(0; -3; -1). А2 (1; 0; -3). А3 (-2; -2; 2), А4 (1; 2; 0).
09. А1(-1; -4; -2). А2 (0; -1; -4). А3 (-3; -3; 1), А4 (0; 2; -1).
10. А1(4; 0; 1). А2 (-1; -1; -1). А3 (-2; 1; 0), А4 (3; 1; -2).
11. А1(-2; -1; -3). А2 (3; 2; 1). А3 (1; -2; 2), А4 (2; 3; 4).
12. А1(-3; 2; -1). А2 (4; -1; 2). А3 (2; 1; 0), А4 (-1; 5; -2).
Литература: Линейная и векторная алгебра. Аналитическая геометрия. Сборник задач по высшей математике. Академия ГА Алматы 2010. Стр 26-29.
|
|