
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгебраическая функция
|
|
К числу алгебраических функций относятся элементарные функции следующего вида:
1. Целая рациональная функция или многочлен
 ,
,
где  — постоянные числа, называемые коэффициентами; n — целое неотрицательное число, называемое степенью многочлена. Очевидно, что эта функция определена при всех значениях х, т. е. определена на бесконечном интервале.
— постоянные числа, называемые коэффициентами; n — целое неотрицательное число, называемое степенью многочлена. Очевидно, что эта функция определена при всех значениях х, т. е. определена на бесконечном интервале.
2. Дробная рациональная функция. Эта функция определяется как отношение двух многочленов: 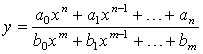 .
.
Дробной рациональной функцией является, например, функция у = 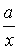 , выражающая обратную пропорциональную зависимость. Ее график изображен на рис. 2. Очевидно, что дробная рациональная функция определена при всех значениях х, кроме тех, при которых знаменатель обращается в нуль.
, выражающая обратную пропорциональную зависимость. Ее график изображен на рис. 2. Очевидно, что дробная рациональная функция определена при всех значениях х, кроме тех, при которых знаменатель обращается в нуль.
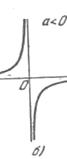 Рис.2
Рис.2
3.Иррациональная функция. Если в формуле у = f(x) в правой части производятся операции сложения, вычитания, умножения, деления и возведения в степень с рациональными нецелыми, показателями, то функция у от х называется иррациональной. Примеры иррациональных функций:
и  т.п.
т.п.
Замечание 1. Перечисленные три вида алгебраических функций не исчерпывают всех алгебраических функций. Алгебраической функцией называется любая функция y = f(x), которая удовлетворяет уравнению вида
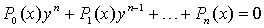 (1)
(1)
где 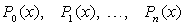 - некоторые многочлены от х.
- некоторые многочлены от х.
Можно доказать, что каждая из функций перечисленных трех видов удовлетворяет некоторому уравнению вида (1), но не всякая функция, удовлетворяющая уравнению вида (1), является функцией одного из перечисленных видов.
Замечание 2. Функция, не являющаяся алгебраической, называется трансцендентной.
Примеры трансцендентных функций: 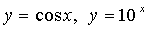 и т.п.
и т.п.
Примеры:
1) Найти  если
если 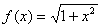
Р е ш е н и е:
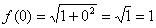 ;
;
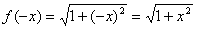 ;
;
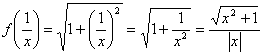 ;
;
 .
.
2) Показать, что 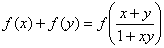 , если
, если 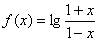 .
.
Р е ш е н и е: найдем 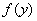 и
и 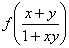 :
:
 ;
;
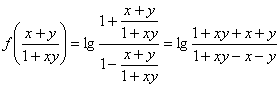 .
.
Далее, найдем  :
:
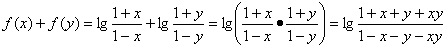 .
.
Сравнивая выражения, полученные для  и
и 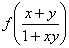 , видим, что действительно
, видим, что действительно 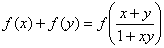 .
.
3) Найти область определения функции 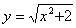 .
.
Р е ш е н и е: выражение 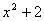 при любом значении х положительно, а поэтому извлечение корня квадратного возможно при любом значении х. Следовательно, областью определения данной функции будет вся числовая ось
при любом значении х положительно, а поэтому извлечение корня квадратного возможно при любом значении х. Следовательно, областью определения данной функции будет вся числовая ось 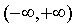 .
.
4) Найти область определения функции  .
.
Р е ш е н и е: очевидно, должно иметь место неравенство  , преобразуя которое получаем
, преобразуя которое получаем 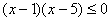 .
.
Последнее неравенство выполняется,
если  или
или 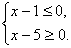
Из первой системы неравенств мы получаем
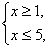 откуда
откуда 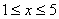 .
.
Из второй системы получаем
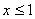 и
и 
т.е. несовместную систему.
Следовательно, областью определения данной функции будет отрезок [1; 5].
5) Найти область определения функции  .
.
Р е ш е н и е: необходимо неравенство
 или
или 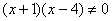
отсюда следует, что 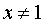 и
и  .
.
Следовательно, областью определения данной функции будет совокупность интервалов 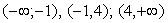 .
.
6) Найти область определения функции 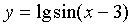 .
.
Р е ш е н и е: чтобы логарифм имел смысл, должно выполнятся неравенство 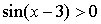 . Синус положителен в I и IIчетвертях и имеет период
. Синус положителен в I и IIчетвертях и имеет период 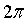 . Поэтому последнее неравенство может быть записано в виде
. Поэтому последнее неравенство может быть записано в виде
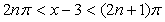 , где
, где 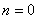 ,
, 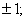
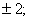
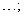
или
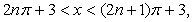 где
где 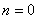 ,
, 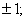
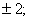
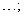
Следовательно, областью определения данной функции будет совокупность интервалов
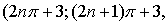 где
где 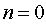 ;
; 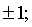

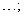
7) Найти область определения функции 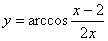
Р е ш е н и е: данная функция определена, если
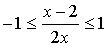
умножим все части неравенства на  . При этом, в случае
. При этом, в случае
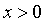 , получаем
, получаем 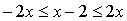 ,
,
а когда 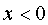 , то
, то  .
.
Первые из этих неравенств можно представить в виде систем
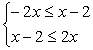 или
или  или
или 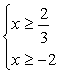
откуда  .
.
Вторые неравенства можно представить в виде систем
 или
или 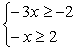 или
или 
откуда  .
.
Следовательно, областью определения данной функции будет совокупность двух бесконечных интервалов  .
.
8) Найти область определения данной функции  .
.
Р е ш е н и е: найдем область определения каждого слагаемого в отдельности. Общая часть этих областей определения будет областью определения данной функции.
Первое слагаемое определено на бесконечном интервале 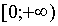 . Для второго слагаемого необходимо выполнение неравенства
. Для второго слагаемого необходимо выполнение неравенства  ,
,
следовательно, оно определено на бесконечном интервале, 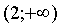 . Для третьего слагаемого необходимо выполнение неравенства
. Для третьего слагаемого необходимо выполнение неравенства  , или
, или  , его область определения – бесконечный интервал
, его область определения – бесконечный интервал  .
.
Сравнивая результаты, видим, что общей частью трех областей определения будет совокупность интервалов 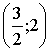 ,
,  .
.
Иногда бывает нужно рассматривать не всю область определения функции, а только некоторую ее часть. Так, зависимость площади Q круга от радиуса R определяется функцией Q=  .Областью определения данной функции при рассмотрении данного геометрического вопроса является бесконечный интервал
.Областью определения данной функции при рассмотрении данного геометрического вопроса является бесконечный интервал 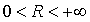 . Областью определения данной функции является бесконечный интервал
. Областью определения данной функции является бесконечный интервал  . Если функция y = f(x) задана аналитически, то она может быть изображена графически на плоскости координат хОу. Так, графиком функции
. Если функция y = f(x) задана аналитически, то она может быть изображена графически на плоскости координат хОу. Так, графиком функции  является парабола (рис.3).
является парабола (рис.3).
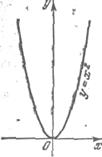
Рис.3
9) Найти функцию, обратную функцию 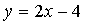 .
.
Р е ш е н и е: разрешим уравнение относительно 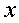
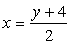 .
.
Полученная функция и будет обратной по отношению к данной, так как при замене 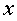 в функции
в функции  на
на 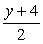 получаем
получаем 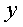 .
.
Действительно, 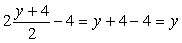 .
.
10) Сложную функцию 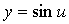 ,
, 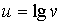 ,
, 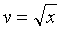 записать в виде одного равенства.
записать в виде одного равенства.
Р е ш е н и е: подставим в функцию  значение
значение 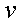 из функции
из функции 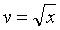 , получим
, получим 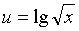 .
.
Подставим полученное значение 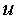 для в функцию
для в функцию 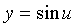 , тогда данная сложная функция примет вид
, тогда данная сложная функция примет вид 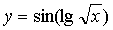 .
.
Итак: определены числовые множества, понятие функции, ее свойства.
|
|