
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Последовательность решения 1 и 2 задач
|
|
1. Опускаем из точки А перпендикуляр на плоскость.
2. Заключаем перпендикуляр в плоскость частного положения Q.
3. Строим линию пересечения плоскостей МN.
4. Находим точку пересечения перпендикуляра с плоскостью К.
5. Определяем натуральную величину перпендикуляра методом
прямоугольного треугольника.
Таблица 10 – Данные для решения задачи 1 (мм)
| № варианта | Координаты точки А | Плоскость Р | ||||
| x | y | z | L | α º | β º | |
| 1, 17 | ||||||
| 2, 18 | ||||||
| 3, 19 | ||||||
| 4, 20 | ||||||
| 5, 21 | ||||||
| 6, 22 | - 40 | |||||
| 7, 23 |
Продолжение таблицы 10
| 8, 24 | ||||||
| 9, 25 | ||||||
| 10, 26 | ||||||
| 11, 27 | ||||||
| 12, 28 | ||||||
| 13, 29 | ||||||
| 14, 30 | -10 | |||||
| 15, 31 | ||||||
| 16, 32 |
Таблица 11 – Данные для решения задачи 2 (мм)
| № варианта | Точка А | Точка В | Точка С | Точка D | ||||||||
| x | y | z | x | y | z | x | y | z | x | y | z | |
| 1, 17 | ||||||||||||
| 2, 18 | ||||||||||||
| 3, 19 | ||||||||||||
| 4, 20 | ||||||||||||
| 5, 21 | ||||||||||||
| 6, 22 | ||||||||||||
| 7, 23 | ||||||||||||
| 8, 24 | ||||||||||||
| 9, 25 | ||||||||||||
| 10, 26 | ||||||||||||
| 11, 27 | ||||||||||||
| 12, 28 | ||||||||||||
| 13, 29 | ||||||||||||
| 14, 30 | ||||||||||||
| 15, 31 | ||||||||||||
| 16, 32 |
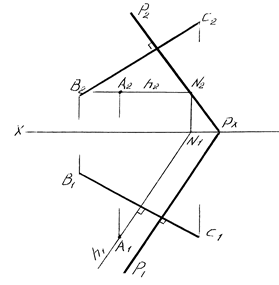
Рисунок 27 – Образец решения задачи 3
Последовательность решения задачи 3
1. Проводим через точку А горизонталь или фронталь плоскости Р
перпендикулярно прямой ВС.
2. Находим фронтальный след горизонтали или горизонтальный след
фронтали.
3. Через полученную точку проводим следы плоскости Р.
Таблица 12 – Данные для решения задачи 3 (мм)
| № варианта | Точка А | Точка В | Точка С | ||||||
| x | y | z | x | y | z | x | y | z | |
| 1, 17 | |||||||||
| 2, 18 | - 8 | ||||||||
| 3, 19 | |||||||||
| 4, 20 | - 25 | ||||||||
| 5, 21 | - 15 | ||||||||
| 6, 22 | |||||||||
| 7, 23 | - 15 | ||||||||
| 8, 24 | |||||||||
| 9, 25 | |||||||||
| 10, 26 |
Продолжение таблицы 12
| 11, 27 | - 35 | ||||||||
| 12, 28 | - 20 | - 40 | |||||||
| 13, 29 | - 15 | ||||||||
| 14, 30 | |||||||||
| 15, 31 | - 15 | - 45 | |||||||
| 16, 32 |
ВОПРОСЫ К ЗАНЯТИЮ
1. Каково условие перпендикулярности прямой и плоскости?
2. Как на эпюре располагаются проекции перпендикуляра к плоскости, если плоскость задана: а – следами, б – не следами?
3. Условие перпендикулярности двух плоскостей.
4. Будут ли перпендикулярны плоскости общего положения, если их следы взаимно перпендикулярны?
5. Как располагаются следы двух перпендикулярных проецирующих плоскостей?
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 5
ГЕОМЕТРИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ТЕНЕЙ.
ПОСТРОЕНИЕ ТЕНЕЙ ОТ ТОЧКИ, ПРЯМОЙ И ПЛОСКОСТИ
|
|