
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
С помощью диаграммы
|
|
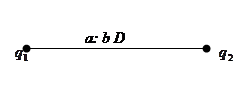 Диаграмма представляет собой геометрический объект (ориентированный граф), состоящий из вершин и дуг. Каждой вершине приписывается состояние машины Тьюринга: таким образом, вершин в диаграмме ровно столько, сколько имеется состояний. Дуге, соединяющей две вершины qi и qj, приписывается некоторый символ a алфавита A и двойка b D так, что запись a qi b qj D образует команду программы машины Тьюринга.
Диаграмма представляет собой геометрический объект (ориентированный граф), состоящий из вершин и дуг. Каждой вершине приписывается состояние машины Тьюринга: таким образом, вершин в диаграмме ровно столько, сколько имеется состояний. Дуге, соединяющей две вершины qi и qj, приписывается некоторый символ a алфавита A и двойка b D так, что запись a qi b qj D образует команду программы машины Тьюринга.
Композиция машин Тьюринга
- Последовательное соединение машин.
Для организации такой работы достаточно построить объединенную таблицу машины Тьюринга, приписав к первой таблице вторую (справа) и заполнив пустые клетки первой таблицы командой перехода к начальному состоянию второй программы.
f(x)=(x+1)*2
| g1 | g2 | g3 | g4 | s1 | s2 | s3 | |
| 1 g1 R | 0 g2 L | 1 g3 L | 1 s1 S | 1 s1 R | 1 s2 L | ||
| 0 g1 R | 1 g3 L | 0 g3 L | 0 s1 S | 0 s1 R | 0 s2 L | ||
| e | e g2 L | 1 g4 S | e g4 R | 0 s2 L | e s3 R |
Итерация (повторение) машин Тьюринга
В этом случае повторяем выполнение одной и той же команды конечное число раз. По окончании первого выполнения на ленте остается промежуточный результат необходимый для второго выполнения и т.д. Для обеспечения второго и последующих выполнений необходимо в некоторые пустые клетки таблицы вписать команду перехода на начало. Во все пустые клетки эту команду вписывать нельзя, так как измененная таким образом программа не сможет заканчиваться.
f(X)=X+L eeeeX*Leeeee
| s1 | s2 | q1 | q2 | q3 | q4 | q5 | |
| 1 s1 L | 1 q1 S | 1 q1 R | e q3 L | 1 q3 L | 1 q4 L | ||
| e | 1 s2 S | e q2 L | e s1 R | e q5 R | |||
| * | * q1 R | * q3 L |
3)  Формализация понятия алгоритма: нормальные алгорифмы Маркова, определение и выполнение. Примеры.
Формализация понятия алгоритма: нормальные алгорифмы Маркова, определение и выполнение. Примеры.
Алгорифмы Маркова (нормальные алгорифмы) используются для представления алгоритмов, преобразующих одну цепочку символов (исходные данные) в другую (результат).
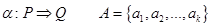
Отличие алгорифмов Маркова в том, что каждый шаг преобразования позволяет выполнить замену не одного символа, а целого слова в исходной цепочке.
Если применив алгоритм 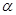 к строке
к строке 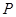 , мы, за конечное число шагов, получили результат
, мы, за конечное число шагов, получили результат  , то такой алгоритм будем называть применимым и обозначать
, то такой алгоритм будем называть применимым и обозначать 
Замены выполняются в соответствии с заданным правилом, которые и будут определять алгоритм. Такой алгоритм называется вербальным.
Расширим алфавит 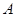 тремя символами «
тремя символами «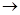 », «
», «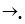 ». «|». Предполагается, что в алфавит
». «|». Предполагается, что в алфавит 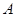 эти символы не входят. В расширенном алфавите можно записывать разные слова, но особенное внимание уделим сломам вида:
эти символы не входят. В расширенном алфавите можно записывать разные слова, но особенное внимание уделим сломам вида: 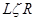 , где
, где 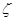 - один из двух символов: стрелка или стрелка с точкой,
- один из двух символов: стрелка или стрелка с точкой, 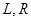 - любая цепочка символов в алфавите
- любая цепочка символов в алфавите 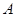 .
.
Если такое правило срабатывает, то в исходной строке отыскивается подстрока 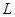 и она целиком заменяется на
и она целиком заменяется на 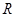 .
.
Для определения алгоритма нужно задать не одно правило, не одну формулу подстановки, а множество, причем необходимо определить порядок их применения. Для этого вводится еще одно понятие схемы алгоритма. Схемой – называется слово в расширенном алфавите, имеющее вид 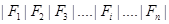 , где
, где 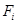 - формулы подстановок. Чем меньше номер, тем выше приоритет. Это значит, что если в цепочке символов, которая преобразуется с помощью алгоритма, встречается несколько подстрок, то применяться будет формула, имеющая минимальный номер.
- формулы подстановок. Чем меньше номер, тем выше приоритет. Это значит, что если в цепочке символов, которая преобразуется с помощью алгоритма, встречается несколько подстрок, то применяться будет формула, имеющая минимальный номер.
Если в строке, которая преобразуется алгорифмом встречается левая часть какой-то формулы 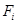 , то это означает, что формула
, то это означает, что формула 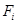 - действует на эту строку. В общем случае в схеме может быть несколько формул, которые действуют на строку, но выбираться будет с большим приоритетом.
- действует на эту строку. В общем случае в схеме может быть несколько формул, которые действуют на строку, но выбираться будет с большим приоритетом.
Если какая-то подстановка действует на исходную строку, причем левая часть встречается в строчке многократно, то формула подстановки применяется один раз. Причем применяется к самому левому вхождению.
При заменах могут использоваться пустые строки
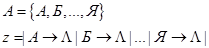
Если в схеме используется несколько правил, в которых правые части совпадают, а левые части являются подстроками, которые можно объединить в какое-то множество, то пишут
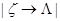 , где
, где 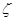 - все элементы от А до Я
- все элементы от А до Я
Пустая строка может встречаться и в левой части. Если есть такие правила, то пустота замениться слева. В этом случае при составлении схемы, нужно думать о том, чтобы алгоритм был применим.
Каким образом алгоритм завершает работу?
Есть несколько вариантов:
1. Не применима ни одна подстановка в схеме (не действует на полученную строку)
2. Выбирается формула подстановки вида: 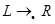 . Такая формула подстановки называется заключительной. После ее применения алгоритм завершает работу. Если в левой части этой формулы используется пустая стока, то эта формула подстановки не должна иметь высокий приоритет и обязательно должна присутствовать заключительная формула с большим приоритетом.
. Такая формула подстановки называется заключительной. После ее применения алгоритм завершает работу. Если в левой части этой формулы используется пустая стока, то эта формула подстановки не должна иметь высокий приоритет и обязательно должна присутствовать заключительная формула с большим приоритетом.
4)  Вычислимые функции. Базовый набор функций и операции над функциями: суперпозиция, примитивная рекурсия, минимизация. Классы вычислимых функций. Примеры.
Вычислимые функции. Базовый набор функций и операции над функциями: суперпозиция, примитивная рекурсия, минимизация. Классы вычислимых функций. Примеры.
При разработке алгоритма (программы) встает несколько вопросов:
1) Является ли задача алгоритмические вычислимой, т.е можно ли построить алгоритм для ее решения.
Каждую задачу, ее решение можно рассматривать как функции, в которой исходные данные преобразуются в результат. Если мы можем построить метод этого преобразования, формализовать его, то такая функция является вычислимой
2) Если функция вычислима, как построить алгоритм?
Попробуем построить алгоритм:
1. Определим базовый набор функций, для которых уже построена машина Тьюринга.
Предположим, что все функции преобразуют целые числа в целые числа.
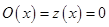 - функция обнуления
- функция обнуления
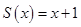 - функция суммы
- функция суммы
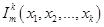 - функция выбора. Выбирает из набора аргументов аргумент с номером
- функция выбора. Выбирает из набора аргументов аргумент с номером 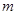
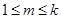
Обозначим этот базовый набор за 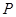
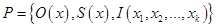
2. В базовом наборе функций определим основные операции. Операции получают функции (а не значения функций) в качестве операндов и дают в результате новые функции. Эти операции также должны быть очевидны с математической точки зрения – не должно возникать сомнения в том, что из вычислимых функций с помощью операций получаются вновь вычислимые функции. Последовательно применяя операции из к множеству функций из 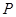 мы будем получать новые функции, которые будут расширять набор
мы будем получать новые функции, которые будут расширять набор 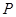 . Следовательно, мы сможем построить бесконечный набор функций.
. Следовательно, мы сможем построить бесконечный набор функций.
Обозначим набор этих операций  . в систему операций
. в систему операций  входят три операции: суперпозиция
входят три операции: суперпозиция  , примитивная рекурсия
, примитивная рекурсия 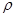 и минимизация
и минимизация 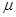 .
.
|
|