Символический метод расчета цепей переменного синусоидального тока

Основным понятием в данном методе является комплексная амплитуда, поэтому его называют также методом комплексных амплитуд. Синусоидальные функции (ток, напряжение, ЭДС) очень просты, но их графическое изображение и операции с ними трудоемки и недостаточно точны. Эти операции можно существенно упростить, если синусоидальные функции времени изобразить комплексными числами.

Из курса математики известно, что любое комплексное число 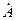можно представить:

а) – в алгебраической форме ;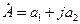

б) – в тригонометрической форме ;

в) – в показательной форме .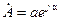

г) – вектором на комплексной плоскости (рис. 3.12), где A –длина (модуль) вектора, 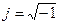– мнимая единица,

Вещественная часть комплексного числа 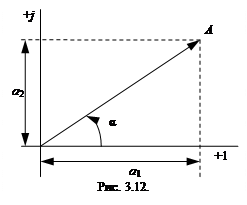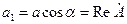(real – реальный, вещественный).

Мнимая часть комплексного числа 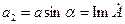(imaginary – мнимый, воображаемый).

Модуль комплексного числа ;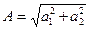

аргумент комплексного числа .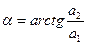

формула Эйлера .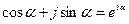

Угол α отсчитывают от положительного направления оси вещественных (ось +1). Положительный угол отсчитывают в направлении, противоположном движению часовой стрелки, отрицательный — в направлении движения часовой стрелки.

Сложение и вычитание комплексных чисел

.

Умножение комплексных чисел

Умножение комплексного числа на число e^{i φ} сводится к повороту вектора на угол φ.

Умножение комплексных величин на + j = e^{j π /2} сводится к повороту вектора против часовой стрелки на угол π /2, а умножение на – j = e^{j π /2} – к повороту вектора на прямой угол по часовой стрелке.

Комплексные числа 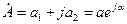и 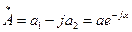называются сопряженными. Произведение сопряженных комплексных чисел вещественно и равно квадрату их модуля

.

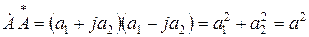Деление комплексных чисел

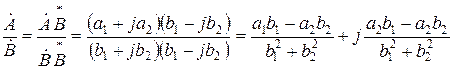
или в показательной форме .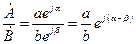

Возведение комплексных чисел в степень

.

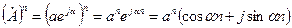Извлечение корня из комплексного числа (n – целое и положительное число)

;

где k – целое число, равное 0, 1, 2, …, (n -1).

Запишем в трех формах выражения для единичных действительных и мнимых комплексных чисел (случай А =1):

,

,

,

.

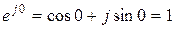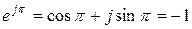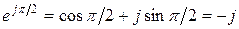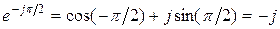Следует обратить внимание на то, что комплексные изображения несут информацию только о двух параметрах синусоиды – амплитуде и фазе, не отражая ее третьего параметра – угловую частоту ω. Поэтому аппарат комплексных чисел применим для анализа цепи, в которой действуют источники одной известной и неизменной угловой частоты ω.

Рассмотрим синусоидальный ток i = I_m sin(ω t +ψ _i) и комплексное число

,

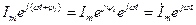модуль и аргумент которого соответственно равны амплитуде и фазе синусоидального тока.

С одной стороны, данное комплексное число представляет аналитическую запись вектора с модулем I_т, вращающегося в комплексной плоскости с постоянной угловой скоростью ω, равной угловой частоте синусоидального тока, в направлении, противоположном движению часовой стрелки.

С другой стороны, данное комплексное число, согласно формуле Эйлера, можно представить в тригонометрической форме:

.

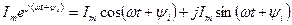Сравнивая последнее с формулой для тока i = I_m sin(ω t +ψ _i) видно, что

,

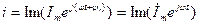т. е. синусоидальный ток равен проекции на ось мнимых чисел вращающегося вектора, изображающего комплексное число.

Таким образом, синусоидальному току i (оригиналу)может быть поставлено в соответствие комплексное число (изображение) 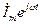. Условная запись такого преобразования имеет вид

Аналогичные преобразования могут быть выполнены для синусоидальных напряжений и ЭДС:

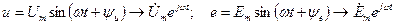
Над комплексными числами, изображающими синусоидальные ЭДС, напряжения и токи, можно производить все алгебраические действия. При сложении и вычитании комплексных чисел удобнее пользоваться алгебраической формой записи, а при умножении, делении, возведении в степень и извлечении корней — показательной формой.

Комплексное число

,

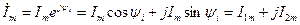модуль и аргумент которого соответственно равны амплитуде и начальной фазе синусоидального тока, называют комплексной амплитудой тока.

Комплексным действующим током (комплексным током)называют комплексное число

.

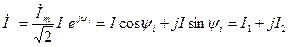Такими же соотношениями связаны комплексные амплитуды и комплексные действующие напряжения и ЭДС.

Комплексное число e^{j ω t} называют множителем вращения. При выполнении условия ω =const взаимное расположение всех векторов (ЭДС, напряжения, тока) не изменяются, поэтому весь процесс рассматривают для момента времени t =0 и множитель вращения в дальнейшем не учитывают, т. к. e^{j ω t} = 0 при t=0. Расчет ведут с использованием комплексных амплитуд или комплексов действующих значений.

Таким образом, при изображении синусоидальных величин комплексными числами в показательной форме записи в качестве модуля следует брать амплитуду (или действующее значение) синусоидальной величины, а в качестве аргумента — ее начальную фазу.

Режим работы электрической цепи переменного тока, как правило, описывается системой дифференциальных уравнений для мгновенных значений синусоидальных токов, напряжений и ЭДС, членами которых могут быть производные любого порядка и интегралы от синусоидальных функций времени. Поскольку производные любого порядка и интегралы от синусоидальных функций также являются синусоидальными функциями, то им, как и синусоидальным токам, напряжениям и ЭДС, можно поставить в соответствие комплексные числа, являющиеся изображениями этих величин. Так, для синусоидального тока, для которого имеем 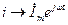, получим

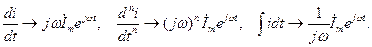
Таким образом, производной от синусоидального тока можно поставить в соответствие комплексное число, изображающее этот синусоидальный ток, умноженное на j ω, а интегралу от синусоидального тока — комплексное число, изображающее синусоидальный ток, деленное на j ω.

Аналогичные преобразования могут быть выполнены и для синусоидальных напряжений и ЭДС.

Комплексный метод расчета электрических цепей синусоидального тока применим только при установившихся режимах работы цепей. Сущность его заключается в том, что, используя указанные преобразования, систему дифференциальных уравнений для действительных функций времени можно заменить системой алгебраических уравнений с комплексными токами, напряжениями и ЭДС. Переход от дифференциальных уравнений к алгебраическим уравнениям с комплексными числами осуществляют заменой в них мгновенных значений тока i, напряжения и, ЭДС е, а также производных и интегралов от них — комплексными числами.

Так как комплексные амплитуды тока, напряжения и ЭДС и комплексные действующие токи, напряжения и ЭДС можно изображать векторами на комплексной плоскости, то расчет электрических цепей полезно сопровождать построением векторных диаграмм, под которыми: понимают совокупность векторов на комплексной плоскости, изображающих синусоидально изменяющиеся функции времени одной и той же частоты и построенных с соблюдением правильной их ориентации относительно друг друга по фазе, что в ряде случаев позволяет выявить ошибки расчета. На векторных диаграммах принято изображать векторы комплексных токов, напряжений и ЭДС или комплексные амплитуды этих величин для момента времени t =0.