Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Разложение вектора по координатным осям

Пусть имеем вектор 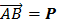. Построим в точке А систему прямоугольных координат Ахуz. Чтобы разложить вектор Р по направлениям осей, нужно построить на этих осях параллелепипед, для которого АВ является диагональю рис2.10.

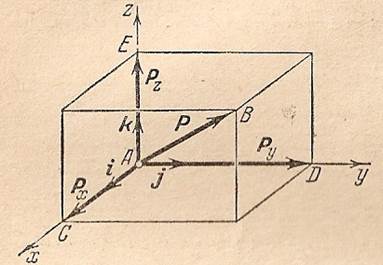
Рис.2.10

Векторы 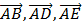называются составляющими данного вектора Р по координатным осям. Обозначив составляющие через , получим:

(2.9)

Следует обратить внимание на различие между составляющими данного вектора по координатным осям и проекциями этого вектора на оси: проекция вектора на ось величина скалярная, а составляющая данного вектора есть также вектор.

Построим единичные векторы, направленные по координатным осям, направленные в положительную сторону. Эти векторы называются единичными координатными векторами (ортами) и обозначаются буквами i, j, k. Задавая векторы i, j, k, мы определяем направления осей выбранной системы координат.

На основании равенства (2.8) можно записать:

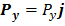, и (2.10)

Подставляя (2.10) в (2.9) получим:

(2.11)

(2.11) называется формулой разложения вектора Р по координатным осям. В формуле разложения вектора по координатным осям скалярные коэффициенты при ортах i, j, k представляют собой проекции этого вектора на эти оси.