
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства математического ожидания и дисперсии
|
|
Если существуют соответствующие моменты, то справедливы следующие свойства математического ожидания и дисперсии:
1. 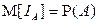 , где
, где 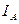 – индикатор события А.
– индикатор события А.
2. Для любых случайных величин X и Y:
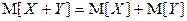
(аддитивное свойство математического ожидания).
Замечание. Для любых случайных величин 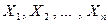 из свойства 2 по индукции выводится:
из свойства 2 по индукции выводится:
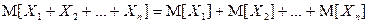 .
.
3. Для любой константы c:
 ,
, 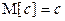 .
.
4. Для любых случайных величин X и Y: если 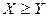 , то
, то 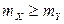 .
.
В частности, если 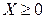 , то
, то 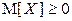 .
.
5. Для любой случайной величины X: если 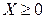 и
и 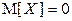 , то
, то 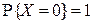 .
.
6. Для любой случайной величины X:
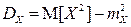 .
.
7. Для любой случайной величины X:
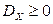
(свойство неотрицательности дисперсии).
8. Для любой константы c:
 ,
, 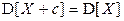 .
.
9. Для любых случайных величин X и Y:
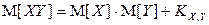 (или
(или  ).
).
В частности, если случайные величины X и Y некоррелированны, то

(мультипликативное свойство математического ожидания).
Замечание. Отметим, что для случайных величин 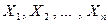 , где
, где 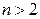 , для выполнения свойства
, для выполнения свойства
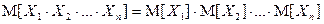
недостаточно условия некоррелированности 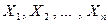 . Однако если случайные величины независимы, то последнее равенство верно.
. Однако если случайные величины независимы, то последнее равенство верно.
10. Для любых случайных величин X и Y:
 .
.
Замечание. Для любых случайных величин 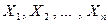 из свойства 11 по индукции выводится:
из свойства 11 по индукции выводится:
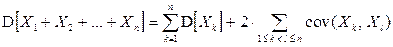 .
.
В частности, если случайные величины X и Y некоррелированны, то
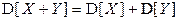
(аддитивное свойство дисперсии).
Замечание. Если случайные величины 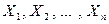 некоррелированны, то
некоррелированны, то
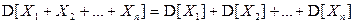 .
.
Отметим также, что поскольку из независимости случайных величин следует их некоррелированность, то свойство 10 выполняется и для независимых случайных величин.
Пример 2.3.20. Известно, что случайная величина имеет биномиальное распределение 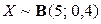 . Найти
. Найти 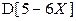 и
и  .
.
Решение. По свойству 8 математического ожидания и дисперсии 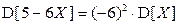 . Поскольку для случайной величины
. Поскольку для случайной величины 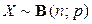 дисперсия
дисперсия  , где по условию задачи
, где по условию задачи  ,
,  ,
, 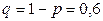 , то
, то
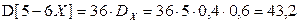 .
.
Вычислим теперь  . Опираясь на свойства 2 и 3 математического ожидания и дисперсии, получим:
. Опираясь на свойства 2 и 3 математического ожидания и дисперсии, получим:
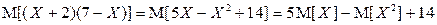 .
.
Поскольку для случайной величины 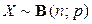 математическое ожидание
математическое ожидание 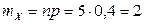 и, по свойству 6,
и, по свойству 6, 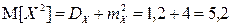 , то
, то
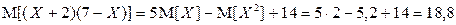 .
.
Ответ: 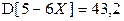 ,
,  .
.
Пример 2.3.21. Функция распределения СВНТ X имеет вид:
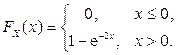
Найти 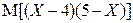 и
и 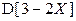 .
.
Решение. По условию задачи случайная величина X распределена по экспоненциальному закону: 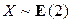 . Поэтому
. Поэтому 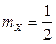 ,
, 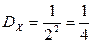 . Найдем вначале
. Найдем вначале 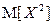 :
: 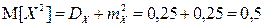 . Тогда:
. Тогда:
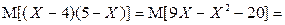
 .
.
По свойству 8 математического ожидания и дисперсии:
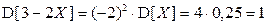 .
.
Ответ: 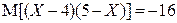 ,
, 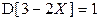 .
.
Пример 2.3.22. Известно, что 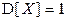 ,
, 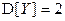 ,
, 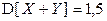 . Найти
. Найти 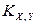 и
и 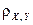 .
.
Решение. Используя формулу для дисперсии суммы
 ,
,
получим  . Тогда
. Тогда
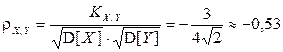 .
.
Ответ: 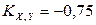 ,
, 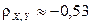 .
.
Пример 2.3.23. На столе налогового инспектора лежат три декларации от представителей трех различных групп населения. Вероятности сокрытия доходов при заполнении декларации для одного представителя каждой группы равны соответственно 0, 05, 0, 1 и 0, 15. Предположим, что сокрытие доходов обнаруживается при проверке в 100% случаев. Найти средний доход государства от проверки этих деклараций, если сумма налагаемого штрафа при обнаружении сокрытия дохода составляет по группам населения 100, 250 и 500 минимальных окладов соответственно.
Решение. Рассмотрим случайную величину X, равную доходу государства от проверки трех деклараций. Тогда X можно представить в виде
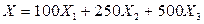 ,
,
где 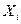 (
(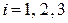 ) индикаторные случайные величины, т.е.
) индикаторные случайные величины, т.е. 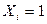 , если подавший декларацию представитель i -й группы населения скрывает доход, и
, если подавший декларацию представитель i -й группы населения скрывает доход, и 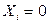 – в противном случае. По условию задачи требуется найти средний доход государства от проверки налоговых деклараций, т.е. математическое ожидание случайной величины X. Воспользуемся свойствами математического ожидания для вычисления
– в противном случае. По условию задачи требуется найти средний доход государства от проверки налоговых деклараций, т.е. математическое ожидание случайной величины X. Воспользуемся свойствами математического ожидания для вычисления 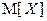 :
:
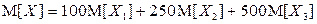 .
.
Поскольку для индикаторных случайных величин  (
(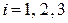 ), то
), то
 .
.
Ответ: средний доход государства от проверки поданных трех деклараций составит 105 минимальных окладов.
Пример 2.3.24. Известно, что случайные величины X и Y (где X – рост наугад взятого взрослого мужчины и Y – его вес) удовлетворительно описываются нормальным законом распределения: 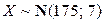 ,
, 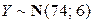 . Ковариация этих признаков равна
. Ковариация этих признаков равна 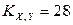 . Считается, что человек страдает избыточным весом, если выполняется неравенство
. Считается, что человек страдает избыточным весом, если выполняется неравенство 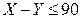 . Найти математическое ожидание и дисперсию характеристики избыточного веса
. Найти математическое ожидание и дисперсию характеристики избыточного веса 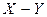 , а также вероятность того, что наугад выбранный мужчина страдает избыточным весом.
, а также вероятность того, что наугад выбранный мужчина страдает избыточным весом.
Решение. Так как случайные величины X и Y распределены нормально, то разность 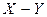 также распределена нормально (Проверьте!). Вычислим параметры этого закона распределения:
также распределена нормально (Проверьте!). Вычислим параметры этого закона распределения:
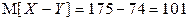 ;
; 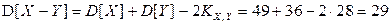 .
.
Таким образом, 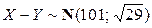 и, следовательно,
и, следовательно,
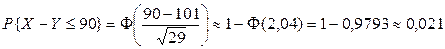 .
.
Ответ: 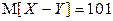 ,
, 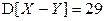 ,
, 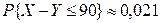 .
.
|
|