
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции многомерных случайных величин
|
|
Функция многомерной случайной величины определяется аналогично тому, как определялась функция одномерной случайной величины. Рассмотрим это на примере двумерной случайной величины. Пусть на вероятностном пространстве (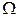 , F, P) задана двумерная случайная величина
, F, P) задана двумерная случайная величина 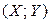 . Предположим, что имеется числовая функция
. Предположим, что имеется числовая функция 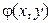 скалярных аргументов x и y. Случайную величину
скалярных аргументов x и y. Случайную величину 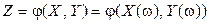 назовем функцией от двумерной случайной величины
назовем функцией от двумерной случайной величины 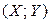 .
.
1. Пусть случайные величины X и Y являются дискретными.
Функция 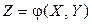 от двумерной дискретной случайной величины
от двумерной дискретной случайной величины 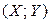 снова является дискретной случайной величиной, принимающей значения
снова является дискретной случайной величиной, принимающей значения 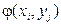 с вероятностями
с вероятностями 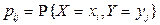 , где
, где 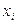 – множество возможных значений компоненты X,
– множество возможных значений компоненты X, 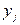 – множество возможных значений компоненты Y. Тогда для нахождения функции распределения можно воспользоваться соотношением
– множество возможных значений компоненты Y. Тогда для нахождения функции распределения можно воспользоваться соотношением
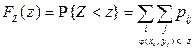
Однако, как правило, удобнее вначале составить ряд распределения случайной величины 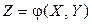 . Чтобы его построить, необходимо исключить все те значения
. Чтобы его построить, необходимо исключить все те значения 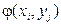 , вероятность которых равна нулю, и объединить в один столбец все одинаковые значения
, вероятность которых равна нулю, и объединить в один столбец все одинаковые значения 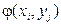 , приписав этому столбцу суммарную вероятность.
, приписав этому столбцу суммарную вероятность.
Пример 2.3.9. Распределение случайного вектора 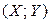 задано таблицей:
задано таблицей:
| Y X | –1 | ||
| –1 | 0, 07 | 0, 1 | 0, 13 |
| 0, 2 | 0, 23 | 0, 27 |
Составить закон распределения случайной величины 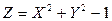 .
.
Решение. Найдем вначале значения функции 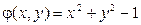 :
:
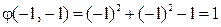 ,
, 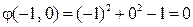 ,
, 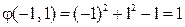 ,
, 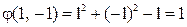 ,
, 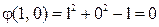 ,
, 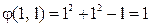 .
.
Значит, случайная величина Z имеет два возможных значения:
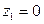 ,
, 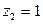 .
.
Вероятность возможного значения 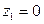 равна сумме вероятностей несовместных событий
равна сумме вероятностей несовместных событий 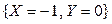 и
и  , т.е.
, т.е. 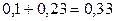 . Вероятность возможного значения
. Вероятность возможного значения 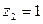 равна сумме вероятностей несовместных событий
равна сумме вероятностей несовместных событий 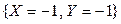 ,
, 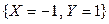 ,
, 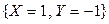 и
и 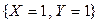 , т.е.
, т.е. 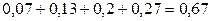 . Поэтому ряд распределения случайной величины Z имеет вид:
. Поэтому ряд распределения случайной величины Z имеет вид:
| Z | ||
| P | 0, 33 | 0, 67 |
Таким образом, случайной величины Z имеет биномиальное распределение 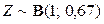 .
.
Ответ: 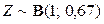 .
.
2. Пусть случайные величины X и Y являются непрерывными.
В случае, когда 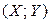 – двумерная непрерывная случайная величина с плотностью
– двумерная непрерывная случайная величина с плотностью 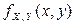 , функция распределения случайной величины
, функция распределения случайной величины 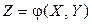 определяется формулой
определяется формулой
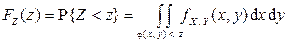 .
.
Область интегрирования здесь состоит из всех точек x и y, для которых 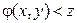 . Найдя функцию распределения
. Найдя функцию распределения 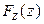 , далее можно дифференцированием по z (в тех точках, в которых
, далее можно дифференцированием по z (в тех точках, в которых 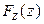 имеет производную по z) найти плотность
имеет производную по z) найти плотность 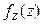 распределения случайной величины Z.
распределения случайной величины Z.
Пример 2.3.10. Случайная точка 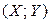 распределена равномерно в квадрате Q со стороной 1 (рис. 2.3.1 а). Найти закон распределения площади Z прямоугольника со сторонами X и Y:
распределена равномерно в квадрате Q со стороной 1 (рис. 2.3.1 а). Найти закон распределения площади Z прямоугольника со сторонами X и Y: 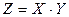 .
.
Решение. Очевидно, что в данном случае случайные величины X и Y независимы (Советуем убедиться в этом самостоятельно!):
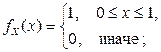
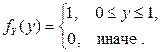
Область интегрирования  заштрихована на рис. 2.3.1 б.
заштрихована на рис. 2.3.1 б.
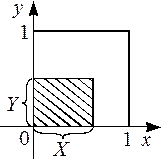
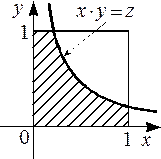
а б
Рис. 2.3.1.
Тогда
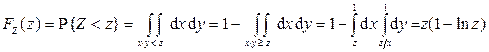 ,
,
где 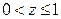 . Таким образом, окончательно получим:
. Таким образом, окончательно получим:
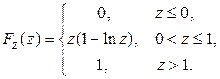
Дифференцируя это выражение по z, получим плотность распределения случайной величины Z:
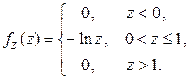
Ответ: 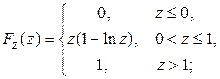
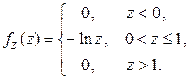
|
|