
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функции одномерных случайных величин
|
|
Функции случайных величин
Функции одномерных случайных величин
Пусть на вероятностном пространстве (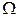 , F, P) задана случайная величина X. Предположим, что имеется числовая функция
, F, P) задана случайная величина X. Предположим, что имеется числовая функция 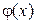 скалярного аргумента x. Случайную величину
скалярного аргумента x. Случайную величину 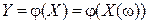 назовем функцией от одномерной случайной величины X. Покажем, как построить закон распределения функции
назовем функцией от одномерной случайной величины X. Покажем, как построить закон распределения функции 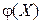 , зная закон распределения случайного аргумента X.
, зная закон распределения случайного аргумента X.
1. Пусть случайная величина X является дискретной.
Функция 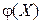 от СВДТ X снова является дискретной случайной величиной, принимающей значения
от СВДТ X снова является дискретной случайной величиной, принимающей значения 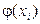 с вероятностями
с вероятностями 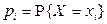 , где
, где 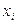 – множество возможных значений СВДТ X. Тогда для нахождения функции распределения можно воспользоваться соотношением
– множество возможных значений СВДТ X. Тогда для нахождения функции распределения можно воспользоваться соотношением
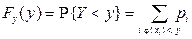 .
.
Однако, как правило, удобнее вначале составить ряд распределения случайной величины  . Чтобы его построить, необходимо объединить в один столбец все одинаковые значения
. Чтобы его построить, необходимо объединить в один столбец все одинаковые значения 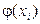 , приписав этому столбцу суммарную вероятность.
, приписав этому столбцу суммарную вероятность.
Пример 2.3.1. Закон распределения случайной величины X имеет вид:
| X | –2 | |||
| P | 0, 2 | 0, 3 | 0, 1 | 0, 4 |
Рассмотрим две числовые функции 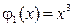 и
и  . Подставляя вместо аргумента x случайную величину Х, получим новые случайные величины
. Подставляя вместо аргумента x случайную величину Х, получим новые случайные величины 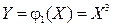 и
и 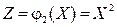 . Построить ряды распределений случайных величин: 1)
. Построить ряды распределений случайных величин: 1) 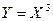 , 2)
, 2)  . Составить их функции распределения.
. Составить их функции распределения.
Решение. 1) Найдем возможные значения случайной величины Y:
 ,
, 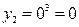 ,
, 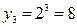 ,
, 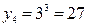 .
.
Тогда ряд распределения случайной величины Y имеет вид:
| Y | –8 | |||
| P | 0, 2 | 0, 3 | 0, 1 | 0, 4 |
Составим теперь функцию распределения случайной величины 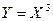 :
:
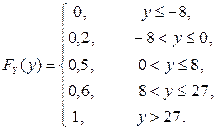
2) Найдем вначале значения функции 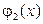 :
:
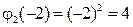 ,
, 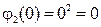 ,
, 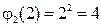 ,
, 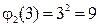 .
.
Значит, случайная величина Z имеет три возможных значения:
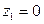 ,
, 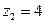 ,
, 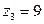 .
.
Вероятность возможного значения 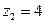 равна сумме вероятностей несовместных событий
равна сумме вероятностей несовместных событий 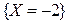 и
и 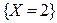 , т.е.
, т.е. 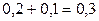 . Поэтому ряд распределения случайной величины Z имеет вид:
. Поэтому ряд распределения случайной величины Z имеет вид:
| Z | |||
| P | 0, 3 | 0, 3 | 0, 4 |
Составим теперь функцию распределения случайной величины  :
:
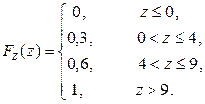
Ответ: 1) 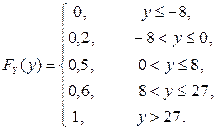 2)
2) 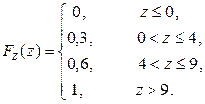
2. Пусть случайная величина X является непрерывной.
Рассмотрим вначале случайную величину 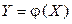 , где
, где 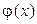 – гладкая строго монотонная функция скалярного аргумента x, а X – СВНТ с плотностью
– гладкая строго монотонная функция скалярного аргумента x, а X – СВНТ с плотностью 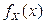 . Тогда плотность распределения
. Тогда плотность распределения 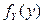 случайной величины Y находится по формуле:
случайной величины Y находится по формуле:
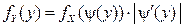 ,
,
где 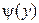 – обратная по отношению к
– обратная по отношению к 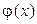 функция.
функция.
Если же 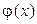 – немонотонная функция на множестве возможных значений X, то следует разбить этот промежуток на такие интервалы, в которых функция
– немонотонная функция на множестве возможных значений X, то следует разбить этот промежуток на такие интервалы, в которых функция 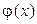 монотонна, и найти плотности распределений
монотонна, и найти плотности распределений 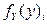 для каждого из интервалов монотонности, а затем представить
для каждого из интервалов монотонности, а затем представить 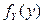 в виде суммы
в виде суммы
 .
.
В частности, если функция 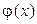 монотонна в двух интервалах, в которых соответствующие обратные функции равны
монотонна в двух интервалах, в которых соответствующие обратные функции равны 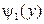 и
и  , то
, то
 .
.
Пример 2.3.2. Найти плотность распределения СВНТ 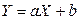 (
(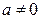 ), где СВНТ X имеет плотность
), где СВНТ X имеет плотность 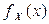 .
.
Решение.  при
при 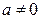 гладкая строго монотонная функция. Тогда обратная функция
гладкая строго монотонная функция. Тогда обратная функция 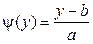 . Отсюда
. Отсюда 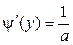 . Таким образом,
. Таким образом,
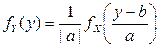 .
.
Ответ: 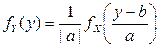 .
.
Пример 2.3.3. Случайная величина X распределена нормально с параметрами m и 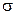 (
(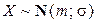 ). Доказать, что линейная функция
). Доказать, что линейная функция 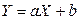 , где
, где 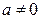 , также распределена нормально, причем
, также распределена нормально, причем  ,
, 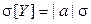 .
.
Решение. Напишем плотность распределения случайной величины X:
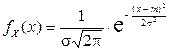 .
.
Применим формулу 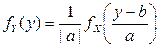 , выведенную в предыдущем примере 2.3.2. Получим
, выведенную в предыдущем примере 2.3.2. Получим
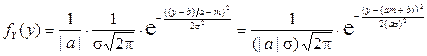 .
.
Отсюда видно, что 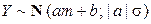 .
.
Пример 2.3.4. Случайная величина X распределена по закону Коши
 .
.
Найти плотность распределения случайной величины 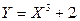 .
.
Решение. 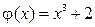 гладкая строго монотонная функция. Тогда обратная функция
гладкая строго монотонная функция. Тогда обратная функция 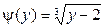 . Отсюда
. Отсюда 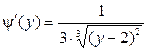 , причем
, причем 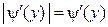 . Значит,
. Значит, 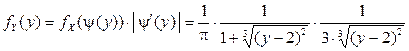 .
.
Таким образом,
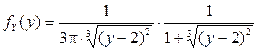 .
.
Ответ: 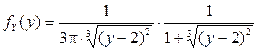 .
.
Пример 2.3.5. Случайная величина X распределена равномерно в интервале 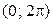 (
( ). Найти плотность распределения случайной величины
). Найти плотность распределения случайной величины 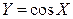 .
.
Решение. Найдем плотность распределения 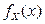 случайной величины X:
случайной величины X:

Из уравнения 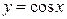 найдем обратную функцию
найдем обратную функцию 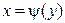 . Поскольку в интервале
. Поскольку в интервале 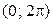 функция
функция 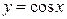 немонотонна, то необходимо разбить этот интервал на интервалы
немонотонна, то необходимо разбить этот интервал на интервалы 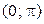 и
и 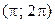 , в которых эта функция монотонна. На интервале
, в которых эта функция монотонна. На интервале 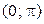 обратная функция
обратная функция  , на интервале
, на интервале 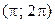 обратная функция
обратная функция  . Тогда искомая плотность распределения может быть найдена из равенства
. Тогда искомая плотность распределения может быть найдена из равенства
 .
.
Найдем производные обратных функций:
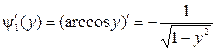 ,
,  .
.
Тогда модули производных равны
 ,
, 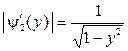 .
.
Учитывая, что 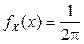 при
при  , получим
, получим
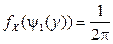 ,
, 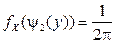 .
.
Отсюда
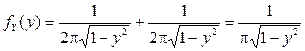 .
.
Так как 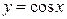 при
при  , то
, то 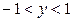 . Таким образом, на интервале
. Таким образом, на интервале  искомая плотность распределения равна
искомая плотность распределения равна 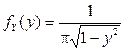 , вне этого интервала
, вне этого интервала 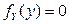 .
.
Ответ: 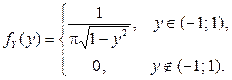
Рассмотрим далее на примерах, как находится функция распределения  случайной величины
случайной величины  , если известна функция распределения
, если известна функция распределения 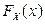 случайной величины X.
случайной величины X.
Пример 2.3.6. Задана функция распределения 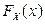 случайной величины X. Найти функцию распределения
случайной величины X. Найти функцию распределения  случайной величины
случайной величины  , если: 1)
, если: 1) 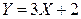 ; 2)
; 2) 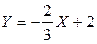 .
.
Решение. 1) По определению функции распределения 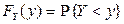 . Поскольку функция
. Поскольку функция 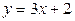 – возрастающая, то неравенство
– возрастающая, то неравенство 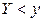 выполняется, если имеет место неравенство
выполняется, если имеет место неравенство 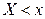 , поэтому
, поэтому
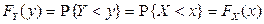 .
.
Из уравнения 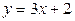 выразим x:
выразим x: 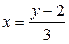 . Тогда
. Тогда
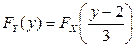 .
.
2) По определению функции распределения 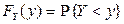 . Поскольку функция
. Поскольку функция  – убывающая, то неравенство
– убывающая, то неравенство 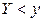 выполняется, если имеет место неравенство
выполняется, если имеет место неравенство  , поэтому
, поэтому
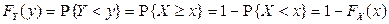 .
.
Из уравнения  выразим x:
выразим x: 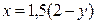 . Тогда
. Тогда
 .
.
Ответ: 1) 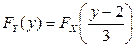 ; 2)
; 2)  .
.
|
|