
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Мода и медиана
|
|
К средним величинам относят также моду и медиану.
Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней (арифметической, гармонической и др.) невозможен или нецелесообразен.
Например, выборочное обследование в г. Омске 12 коммерческих пунктов обмена валюты позволило зафиксировать различные цены за доллар при его продаже (данные на 10 октября 1995г. при биржевом курсе доллара -4493руб).
| № пункта обмена валюты | ||||||||||||
| Цена за 1 дол., руб. |
В силу того, что исследователь не располагает данными об объеме продаж в каждом обменном пункте, расчет средней арифметической с целью определения средней цены за доллар нецелесообразен. Однако можно определить то значение признака, которое носит название медиана (Ме). Медиана лежит в середине ранжированного ряда и делит его пополам.
Расчет медианы по несгруппированным данным производится следующим образом:
а) расположим индивидуальные значения признака в возрастающем порядке:
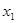
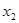
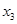
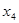

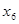
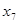
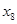
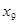
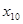

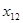
4500 4500 4535 4540 4550 4560 4560 4560 4560 4570 4570 4570
б) определим порядковый номер медианы по формуле:
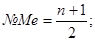
в нашем примере  это означает, что медиана в данном случае расположена между шестым и седьмым значениями признака в ранжированном ряду, так как ряд имеет четное число индивидуальных значений. Таким образом, Ме равна средней арифметической из соседних значений: 4550, 4560.
это означает, что медиана в данном случае расположена между шестым и седьмым значениями признака в ранжированном ряду, так как ряд имеет четное число индивидуальных значений. Таким образом, Ме равна средней арифметической из соседних значений: 4550, 4560.
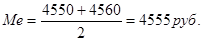
в) рассмотрим порядок вычисления медианы в случае нечетного числа индивидуальных значений.
Допустим, мы наблюдаем не 12, а 11 пунктов обмена валюты, тогда ранжированный ряд будет выглядеть следующим образом (отбрасываем 12-й пункт):
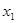
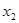
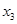
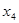

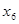
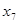
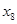
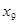
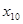

4500 4500 4535 4540 4550 4560 4560 4560 4560 4570 4570
Номер медианы: №Ме = 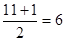 ;
;
на шестом месте стоит 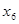 = 4560, который и является медианой: Ме=4560. По обе стороны от нее находится одинаковое число пунктов.
= 4560, который и является медианой: Ме=4560. По обе стороны от нее находится одинаковое число пунктов.
Мода - это наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака.
В нашем случае модальной ценой за доллар можно назвать 4560 руб.: это значение повторяется 4 раза, чаще, чем все другие.
На практике моду и медиану находят, как правило, по сгруппированным данным. В результате группировки был получен ряд распределения банков по величине полученной прибыли за год (табл. 3.6.).
Таблица 3.6.
Группировка банков по величине полученной прибыли за год
| Размер прибыли, млн. руб. | Число банков | Накопительные частоты |
| 3, 7 - 4, 6 | ||
| 4, 6 - 5, 5 | 6 (2+4) | |
| 5, 5 - 6, 4 | 12 (2+4+6) | |
| 6, 4 - 7, 3 | - | |
| 7, 3 - 8, 1 | - | |
| Итого | - |
Для определения медианы надо подсчитать сумму накопительных частот. Наращивание итого продолжается до получения накопительной суммы частот, превышающей половину суммы частот. В нашем примере сумма накопленных частот (12), превышающая половину всех значений (20: 2). Этому значению соответствует медианный интервал, который содержит медиану (5, 5 - 6, 4). Определим ее значение по формуле:

где 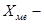 начальное значение интервала, содержащего медиану;
начальное значение интервала, содержащего медиану;
 - величина медианного интервала;
- величина медианного интервала;
f - сумма частот ряда;
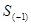 - сумма накопительных частот, предшествующих медианному интервалу;
- сумма накопительных частот, предшествующих медианному интервалу;
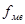 - частота медианного интервала.
- частота медианного интервала.
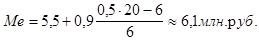
Таким образом, 50% банков имеют прибыль 6, 1 млн. руб., а 50% банков - более 6, 1 млн. руб.
Наибольшая частота соответствует также интервалу 5, 5 - 6, 4, т.е. мода должна находиться в этом интервале. Ее величину определим по формуле:

где  - начальное значение интервала, содержащего моду;
- начальное значение интервала, содержащего моду;
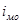 - величина модального интервала;
- величина модального интервала;
 - частота модального интервала;
- частота модального интервала;
 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному;
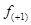 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Приведенная формула моды может быть использована в вариационных рядах с равными интервалами.
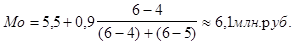
Таким образом, в данной совокупности наиболее часто встречается размер прибыли 6, 10 млн. руб.
Медиану и моду можно определить графически. Медиана определяется по кумуляте (рис. 3.1.). Для ее построения надо рассчитать накопительные частоты и частости. Накопительные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение, и определяется последовательным суммированием частот интервалов. При построении кумулятыы интервального ряда распределения нижней границе первого интервала соответствует частота, равная нулю, а верхней границе - вся частота данного интервала. Верхней границе второго интервала соответствует накопительная частота, равная сумме частот первых двух интервалов, и т.д.
Построим кумулятивную кривую по данным табл. 6 о распределении банков по размеру прибыли.
 S накопительные частоты
S накопительные частоты
20_
_
16_
_

 12_
12_
_
8 _


 _
_
4 _
 |


3, 7-4, 6 4, 6-5, 5 5, 5-6, 4 6, 4-7, 3 7, 3-8, 2 Х прибыль
медиана

Рис. 3.1. Кумулята ряда распределения банков по размеру прибыли:
х - размер прибыли, млн. руб.,
S - накопленные частоты.
Для определения медианы высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.
Мода определяется по гистограмме распределения. Гистограмма строится так:
на оси абсцисс откладываются равные отрезки, которые в принятом масштабе соответствуют величине интервалов вариационного ряда. На отрезках строятся прямоугольники, площади которых пропорциональны частотам (или частостям) интервала.
На рис. 3.2. Изображена гистограмма ряда распределения банков по размеру прибыли (по данным табл. 3.6.).
 |


 f
f

 6 _
6 _
 _
_
4 _

 _
_
2 _
_


 S S
S S
3, 7-4, 6 4, 6-5, 5 5, 5-6, 4 6, 4-7, 3 7, 3-8, 2 Х
мода
 |
Рис. 3.2. Распределение коммерческих банков по размеру прибыли:
х - размер прибыли, млн. руб.,
f - число банков.
Для определения моды правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника - с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.
|
|