
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дискретные случайные величины.
|
|
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайная величина – это величина, которая в результате эксперимента (опыта, испытания) принимает одно из своих возможных значений, причем заранее неизвестно, какое именно.
Примеры случайных величин:
· число дефектных деталей в партии при контроле качества;
· процент завершенного строительства жилого дома спустя 6 месяцев;
· число клиентов операционного отдела банка в течение рабочего дня;
· число продаж автомобилей в течение месяца.
Случайные величины обозначаются заглавными латинскими буквами: X, Y, Z и тому подобными. Строчные буквы используются для обозначения определенных значений случайной величины. Например, случайная величина X принимает значения x 1, x 2, …, xn..
Среди случайных величин различают дискретные и непрерывные случайные величины.
Дискретные случайные величины.
Дискретной случайной величиной называют случайную величину, которая принимает конечное или бесконечное (но счетное) число отдельных, изолированных возможных значений с определенными вероятностями.
Дискретной называют случайную величину, которая может принимать отдельные значения с определенными вероятностями.
Например, число студентов на лекции – дискретная случайная величина.
Закон распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.
Закон распределения дискретной случайной величины можно задать:
1. таблично – рядом распределения;
2. графически;
3. формулой.
Рядом распределения называется совокупность всех возможные значения этой случайной величины х1, х2, …, xn с соответствующими им вероятностями р1, р2, …, рn. Он может быть задан в виде таблицы:
| хi | х1 | х2 | … | хn |
| рi | p1 | р2 | ... | рn |
При этом вероятности рi удовлетворяют условию: 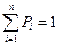 .
.
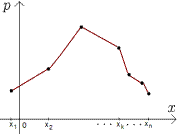 Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины (хi) откладываются по оси абсцисс, а вероятности рi – по оси ординат; точки Аi c координатами (хi, рi) соединяются ломаными линиями.
Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины (хi) откладываются по оси абсцисс, а вероятности рi – по оси ординат; точки Аi c координатами (хi, рi) соединяются ломаными линиями.
Функцией распределения случайной величины Х называется функция F(х), значение которой в точке х равно вероятности того, что случайная величина Х будет меньше этого значения х, то есть F(х) = Р (Х< х).
Функция распределения F(х) для дискретной случайной величины вычисляется по формуле 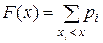
Суммирование ведется по всем значениям i, для которых хi < х.
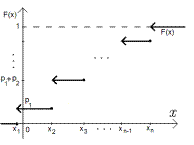 Функция распределения и её график:
Функция распределения и её график:
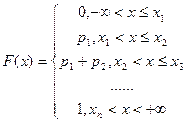
Характеристики дискретной случайной величины:
I. Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех возможных значений величины Х на соответствующие вероятности:
М(Х) = x1•p1 + x2•p2 + … + xn•pn.
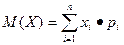
Свойства математического ожидания:
1. Математическое ожидание может быть как положительным, так и отрицательным числом.
2. Математическое ожидание постоянной величины С равно этой постоянной, т.е. М(С) = С.
3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий этих величин, т.е.
М(X+Y+...+W)=М(X)+М(Y)+...+М(W).
4. Математическое ожидание произведения двух или нескольких взаимно независимых случайных величин равно произведению математических ожиданий этих величин, т.е. М(XY)=M(X) × M(Y).
5. Математическое ожидание произведения случайной величины на постоянную С равно произведению математического ожидания случайной величины: М(СХ) = С× М(Х).
II. Дисперсией D(X) дискретной случайной величины Х называется математическое ожидание квадрата отклонения случайной величины Х от ее математического ожидания
D(X) = M [X – M(X)]2= M (X2) – [M(X)]2.
Свойства дисперсии:
1. Дисперсия постоянной величины всегда равна нулю: D(С) = 0.
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СX) = С2 D(X).
3. Дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсией: D(X +Y) = D(X) + D(Y).
III. Средним квадратическим отклонением s(Х) случайной величины Х называется корень квадратный из ее дисперсии: 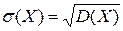
Пример 1. Найти величину S, математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение s(Х) дискретной случайной величины Х, заданной законом распределения в таблице:
| Х | -5 | |||
| р | 0, 4 | S | 0, 1 | 0, 2 |
Решение.
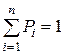 , 0, 4+S+0, 1+0, 2=1, S=1-0, 4-0, 1-0, 2=0, 3.
, 0, 4+S+0, 1+0, 2=1, S=1-0, 4-0, 1-0, 2=0, 3.
Математическое ожидание М(Х) вычисляется по формуле:
М(Х) = x1· p1 + x2· p2 + … + xn· pn.
М(Х) = - 5× 0, 4 + 2× 0, 3 + 3× 0, 1 + 4× 0, 2 = - 0, 3.
Дисперсия вычисляется по формуле: D(Х) = М(Х2) - [М(Х)]2.
Закон распределения Х2 представлен в таблице:
| Х2 | ||||
| р | 0, 4 | 0, 3 | 0, 1 | 0, 2 |
Математическое ожидание М(Х2) вычисляется по формуле:
М(Х2) = 25× 0, 4 + 4× 0, 3 + 9× 0, 1 + 16× 0, 2 = 15, 3.
Искомая дисперсия: D(Х) = М(Х2) - [М(Х)]2 = 15, 3 -(-0, 3)2 = 15, 21.
Тогда среднее квадратическое отклонение будет: 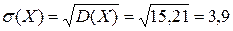 .
.
|
|