
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Количество опечаток на 100 страницах текста.
|
|
Дискретные случайные величины (ДСВ).
1. Примеры ДСВ.
2. Способы задания ДСВ.
2.1. Закон распределения ДСВ.
2.2. Функция распределения ДСВ.
3. Основные характеристики ДСВ.
3.1. Математическое ожидание.
3.2. Дисперсия. Среднее квадратическое отклонение.
4. Примеры распределения ДСВ:
4.1. Биномиальное распределение;
4.2. Геометрическое распределение;
4.3. Гипергеометрическое распределение;
4.4. Пуассоновское распределение.
5. Многомерные ДСВ.
1.
Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая несёт следующие возможные значения: О, 1, 2,.... 100.
Число вызовов, поступивших от абонентов на телефонную станцию в течение определенного промежутка времени,
Количество выпадений герба при 100 бросаниях монеты,
количество опечаток на 100 страницах текста.
2.1.
Для дискретной случайной величины X закон распределения может быть задан в форме таблицы, где х 1, х2, ... — возможные значения величины X, а р1, р2,... — их вероятности. А именно р1 есть вероятность значения х1 (или р1 - что то же самое, вероятность события X = x1), р2 есть вероятность значения х2 и т. д.
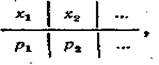
Числа р1, р2,... связаны соотношением, которое вытекает из того факта, что события попарно несовместны, а их сумма есть событие достоверное (при каждом осуществлении опыта величина X принимает одно и только одно из своих значений т. е. наступает одно и только одно из событий). Другими словами, приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события х 1, х2, ... образуют полную группу. Следовательно, сумма вероятностей этих событии, т. е. сумма вероятностей второй строки таблицы, равна единице:
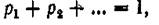
Если множество возможных значений X бесконечно (счетно), то ряд р1 + р2+... сходится и его сумма равна единице.
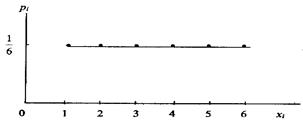
Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (хi, pi), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
При бросании игральной кости случайная величина принимает значения 1, 2, 3, 4, 5, 6, которая задается следующей таблицей:
| xi | ||||||
| pi | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
◄ Задача: По мишени производится 4 независимых выстрела с вероятностью попадания при каждом выстреле р = 0, 8. Требуется: а) найти закон распределения дискретной случайной величины Х, равной числу попаданий в мишень; б) найти вероятности событий: 1 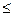 х
х 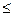 3; х > 3; в) построить многоугольник распределения.
3; х > 3; в) построить многоугольник распределения.
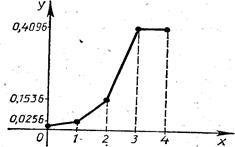
Решение: а) Возможные значения случайной величины х: 0, 1, 2, 3, 4. Соответствующие вероятности вычисляем по формуле Бернулли:
p0 = p (x=0) = C40 0.80 0.24 = 0.0016
p1 = p (x=1) = C41 0.81 0.23 = 0.0256
p2 = p (x=2) = C42 0.82 0.22 = 0.1536
p3 = p (x=3) = C43 0.83 0.21 = 0.4096
p4 = p (x=4) = C44 0.84 0.20 = 0.4096
Закон распределения X представится таблицей:




 xi 0 1 2 3 4
xi 0 1 2 3 4
pi 0, 0016 0, 0256 0, 1536 0, 4096 0, 4096
Проверка: 0, 0016 + 0, 0256 + 0, 1536 + 0, 4096 + 0, 4096 = 1.
б) Вероятности событий 1 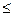 x
x 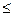 3 и x > 3 равны:
3 и x > 3 равны:
р (1 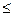 x
x 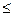 3) == р ({1, 2, 3}) = p1 + р2 + р3 = 0, 0256 + 0, 1536 + 0, 4096 = =0, 5888;
3) == р ({1, 2, 3}) = p1 + р2 + р3 = 0, 0256 + 0, 1536 + 0, 4096 = =0, 5888;
р (х > 3) = р ({4}) = p4 = 0, 4096.
в) Многоугольник распределения представлен на рисунке
►
.
◄ Задача: В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X — стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение. Напишем возможные значения X: х1=50, х2= I, х3=0. Вероятности этих возможных значений таковы: р1=0, 01, р2=0, 1, р3=0, 89.
Напишем искомый закон распределения:
X 50 10 0
р 0, 01 0, 1 0, 89
Контроль: 0, 01+0, 1+0, 89=1.►
◄ Задача. В денежной лотерее выпущено 1000 билетов. Среди 1000 билетов 10 билетов дают выигрыш 100 рублей, 20 билетов дают выигрыш 50 рублей, 40 билетов дают выигрыш 25 рублей, 50 билетов дают выигрыш 10 рублей, 80 билетов дают выигрыш 5 рублей, 100 билетов дают выигрыш 1 рубль, 700 билетов выигрыша не дают. Х - ДСВ - сумма возможного выигрыша для владельца одного билета.
Решение. Закон распределения этой случайной величины зададим следующей таблицей:
| xi | |||||||
| pi | 0, 7 | 0, 1 | 0, 08 | 0, 05 | 0, 04 | 0, 02 | 0, 01 |
Контрольная сумма  = 0, 7+0, 1+0, 08+0, 05+0, 04+0, 02+0, 01 = 1
= 0, 7+0, 1+0, 08+0, 05+0, 04+0, 02+0, 01 = 1
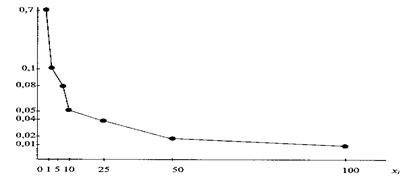 ►
►
2.2.
Функция F (х), определенная для любого х Î R равенством F (х) = р (Х < х) называется функцией распределения случайной величины Х. Если функция распределения F(х) задана, то вероятность события x1≤ X < х2 вычисляется по формуле p(x1≤ X < х2) = F(x2) - F(x1).
Формула для функции распределения F(х) дискретной случайной величины x:
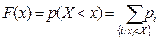
График функции F(x) представляет собой ступенчатую линию. Скачки, функции F(х) в точках х – x1, x2... (x1< x2< …) равны соответствующим вероятностям p1, p2, …
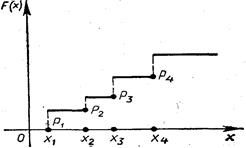
3.1.
Математическое ожидание дискретной случайной величиныопределяется по формуле
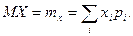
Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть абсолютно сходящимся (в противном случае говорят, что случайная величина не имеет математического ожидания)
◄ Задача. При бросании игральной кости случайная величина X принимает значения 1, 2, 3, 4, 5, 6. Она задается таблицей:
| xi | ||||||
| pi | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Решение. 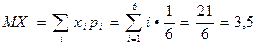 .
.
Как убедимся позднее, если много раз бросить игральную кость и подсчитать среднее 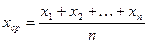 , то это среднее будет мало отличаться от 3, 5.►
, то это среднее будет мало отличаться от 3, 5.►
◄ Задача. В денежной лотерее выпущено 1000 билетов. Среди 1000 билетов 10 билетов дают выигрыш 100 рублей, 20 билетов дают выигрыш 50 рублей, 40 билетов дают выигрыш 25 рублей, 50 билетов дают выигрыш 10 рублей, 80 билетов дают выигрыш 5 рублей, 100 билетов дают выигрыш 1 рубль, 700 билетов выигрыша не дают. Х- ДСВ - сумма возможного выигрыша для владельца одного билета. Закон распределения этой случайной величины зададим следующей таблицей:
| xi | |||||||
| pi | 0, 7 | 0, 1 | 0, 08 | 0, 05 | 0, 04 | 0, 02 | 0, 01 |
Решение. M(X)= 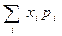 =0•0, 7+1•0, 1+5•0, 08+10•0, 05+25•0, 04+50•0, 02+100•0, 01 = 0+0, 1+0, 4+0, 5+1+1+1 = 4. ►
=0•0, 7+1•0, 1+5•0, 08+10•0, 05+25•0, 04+50•0, 02+100•0, 01 = 0+0, 1+0, 4+0, 5+1+1+1 = 4. ►
◄ Задача. Вероятность появления события А в одном испытании равна р. Найти математическое ожидание числа появлений события А в одном испытании, q = 1 - р.
| xi | ||
| pi | Q | p |
Решение. М(Х)= 1 • p + 0 • q = p. ►
3.2.
Дисперсия дискретной случайной величиныопределяется по формуле 
Сумма берется по всем значениям, которые принимает случайная величина. Ряд должен быть сходящимся (в противном случае говорят, что случайная величина не имеет дисперсии). Среднее квадратическое отклонение находится по формуле 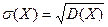 .
.
4.
Хотя можно представить себе бесконечное разнообразие случайных величин, законов распределения гораздо меньше.
Часто случайные величины имеют подобные законы распределения, и отличаются только одной или несколькими постоянными. Эти постоянные называются параметрами распределения.
Хотя в принципе возможны самые разные законы распределения, здесь будут рассмотрены несколько наиболее типичных законов. Важно обратить внимание на условия, в которых они возникают, параметры и свойства этих распределений.
4.1
Пусть производится n независимых испытаний, каждое из которых заканчивается либо “успехом” либо “неуспехом”. Пусть в каждом испытании (опыте) вероятность успеха p, а вероятность неуспеха q = 1- p. Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.
Для нахождения закон распределения величины X требуется определить всевозможные значения X и их вероятности. Очевидно, событие А в n испытаниях может либо не появиться, ибо появиться 1 раз, либо 2 раза,..., либо n раз. Таким образом, возможные значения X таковы: х1 = 0, х 2= 1, х3=2,..., хn+1=n. Соответствующие в ероятности для возможных значений находятся по формуле Бернулли (если n≤ 10):
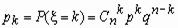 , 0 < p < 1, k = 0, 1, …, n,
, 0 < p < 1, k = 0, 1, …, n, 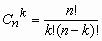 ,
,
| xi | … | k | … | n | |||
| pi | Р0 | p1 | р2 | … | pk | … | рn |
M(X)=  =
= 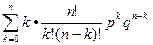 =
= 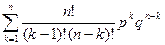 =
= 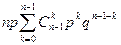 = np.
= np.
D(X)= 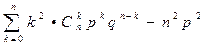 =
= 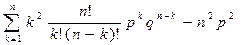 =
= 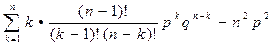 =
=  =
= 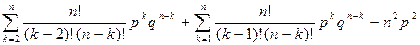 =
= 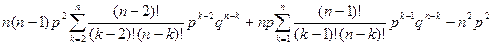 =n(n–1)p2+np–n2p2 = np–np2 = npq.
=n(n–1)p2+np–n2p2 = np–np2 = npq.
Параметры распределения: n, р.
◄ Задача Кость бросают 5 раз, какова вероятность того, что 6 очков выпадет дважды?
Решение. n = 5, m = 2, p = 1/6, q = 5/6
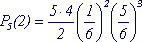 ►
►
◄ Задача: В урне 7 шаров, из которых 4 белых, а остальные черные. Из этой урны наудачу извлекаются 3 шара; X - число извлеченных белых шаров. Найдите закон распределения дискретной случайной величины X и вероятность события X 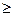 2.
2.
Рeшение. Возможные значения случайной величины X: 0, 1, 2, 3. Соответствующие им вероятности p0, р1, p2, р3, подсчитаем классическим способом:
p0 = p(X=0) = C40*C33 / C73 = 1/35, p1 = p(X=4) = C41*C32 / C73 = 12/35
p2 = p(X=2) = C42*C31 / C73 = 18/35, p3 = p(X=3) = C43*C30 / C73 = 4/35
Закон распределения X:
| xi | ||||
| pi | 1/35 | 12/35 | 18/35 | 4/35 |
Вероятность события X> = 2 равна: P(X> =2) = p({2, 3}) = 18/35 +4/35 = 22/35 ►
4.2.
Со схемой испытаний Бернулли можно связать еще одну случайную величину Х - число испытаний до первого успеха. Эта величина принимает бесконечное множество значений от 0 до + 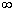 и ее распределение определяется формулой
и ее распределение определяется формулой
pk = P (Х = k) = qk- 1 p, 0 < p < 1, k =1, 2, …,
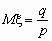 ,
, 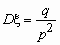 .
.
4.3.
Пусть заданы натуральные числа m, n, s, причем m< =s< =n. Если возможными значениями дискретной случайной величины X являются 0, 1, 2,..., m и соответствующие им вероятности выражаются по формуле 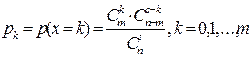 , то говорят, что случайная величина х имеет гипергеометрический закон распределения.
, то говорят, что случайная величина х имеет гипергеометрический закон распределения.
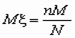 ,
, 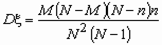 .
.
Замечание. Гипергеометрическое распределение играет важную роль, например, в статистическом контроле качества. Предположим, что произведенные изделия (например, лампочки) разбиты на партии в N штук каждая (например, по ящикам вместимостью в N лампочек). Каждая партия содержит некоторый процент бракованных изделий, который, возможно равен и нулю (например, лампочки с недостаточным сроком годности).
4.4.
Ряд распределения случайной величины Х, распределенной по закону Пуассона, выглядит следующим образом:
| хm | … | m | … | |||
| Pm | e-a | 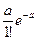
| 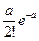
| … | 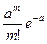
| … |
На рис. представлены многоугольники распределения случайной величины Х по закону Пуассона, соответствующие различным значениям параметра а.

Пуассоновское распределение c параметром λ имеет случайная величина Х, принимающая целые неотрицательные значения k = 0, 1, 2, … с вероятностями p k:
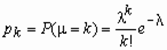 ,
, 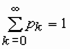 ,
,
M(X) = 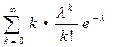 =
= 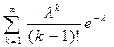 =
= 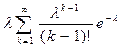 = l;
= l;
Таким образом, параметр λ представляет собой не что иное, как математическое ожидание случайной величины Х.
D(X)= 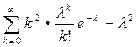 =
= 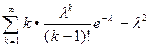 =
=  =
= 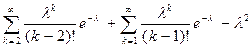 =
= 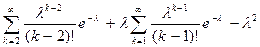 =
= 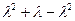 = l. λ > 0 - параметр распределения.
= l. λ > 0 - параметр распределения.
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию.
Распределению Пуассона подчиняются очень многие случайные величины, встречающиеся в науке и практической жизни.
◄ Задача: Завод отправил на базу 500 доброкачественных изделий. Вероятность повреждения каждого изделия в пути равна 0, 002. Найдите закон распределения случайной величины х, равной числу поврежденных изделий, и найдите вероятности следующих событий:
А - повреждено менее 3 изделий;
В - повреждено более 2 изделий;
С - повреждено хотя бы одно изделие.
Решение. Возможные значения х: 0, 1, 2,..., 500; так как n = 500 велико, а р = 0, 002 мало, то, положив k == 500 • 0, 002 = 1, вычислим вероятности Рk=Р(х = k) приближенно по формуле Пуассона: pk = (lk / k!) * e-l = 1/(k! e), k =0, 1, 2, …, 500. Закон, распределения случайной величины х приближенно имеет вид:
| xk | … | |||||
| pk | 1/e | 1/e | 1/2e | 1/6e | … | 1/500! e |
или
| xk | … | |||||
| pk | 0.368 | 0.368 | 0.184 | 0.061 | … | 0.000 |
Используя полученную таблицу, находим вероятности событий А, В и С: р(А) = р (х < 3) = р({0, 1, 2}) = 0, 368 + 0, 368+0, 184 = 0, 92;
р (B) = р (х > 2) = l - p(x< =2) = l - p({0, 1, 2}) = 0, 08;
p(C) =p(x > =1) =1 - p(х< =0) = 1-p({0})=1-0, 368 = 0, 632. ►
5.
Рассмотрим испытание, результатом которого является появление двух чисел из некоторого конечного либо счетного множества пар чисел. Это испытание физически может быть одним испытанием, а также может быть композицией двух испытаний, каждое из которых порождает одномерную дискретную величину.
Двумерной случайной величиной называется система из двух одномерных случайных величин X, Y, где как X, так и Y являются дискретными случайными величинами. В пространстве элементарных событий дискретной случайной величины (X, Y) определим сложное событие A: В результате испытания над двумерной случайной величиной (X, Y), случайная величина X приняла значение xi, случайная величина Y - любое значение. Вводим сложное событие B: В результате испытания над двумерной случайной величиной (X, Y), случайная величина Y приняла значение yj.
Многомерная случайная величина является дискретной, если каждая компонента случайного вектора может принимать только конечное или счетное множество определенных значений.
Случайные величины могут быть зависимыми и независимыми. Для дискретных случайных величин X и Y с матрицей совместного распределения { p ij} условие независимости p ij = P(X = xi, Y = yj)= P(X = xi) P(Y = yj), для всех i = 1, 2, …, n, j = 1, 2, …, m.
Пусть дана двумерная случайная величина (x, h ) с распределением
| y 1 | y 2 | ... | y m | |
| x 1 | p 11 | p 12 | ... | p 1 m |
| x 2 | p 12 | p 12 | ... | p 2 m |
| ... | ... | ... | pij | ... |
| xn | pn 1 | pn 2 | ... | pnm |
Тогда распределения случайных величин x и h имеют соответственно вид:
| x | x 1 | x 2 | ... | x n |
| p 1· | p 2· | ... | pn· |
| h | y 1 | y 2 | ... | y n |
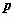
| p· 1 | p· 2 | ... | p·n |
точка ∙ в индексе означает суммирование по строкам или по столбцам:
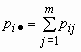 ,
,  .
.
Условным распределением случайной величины  при условии, что случайная величина
при условии, что случайная величина 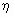 приняла значение
приняла значение 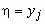 , называется распределение:
, называется распределение:
| x | x 1 | x 2 | ... | x n |
| p | 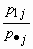
| 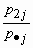
| ... | 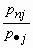
|
Нетрудно убедиться, что сумма вероятностей величины  в этом распределении равна единице:
в этом распределении равна единице: 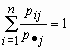 для всех j = 1, 2, …, m. Совершенно аналогично условным распределением случайной величины
для всех j = 1, 2, …, m. Совершенно аналогично условным распределением случайной величины 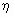 при условии, что случайная величина
при условии, что случайная величина  приняла значение
приняла значение 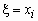 , называется распределение:
, называется распределение:
| h | y 1 | y 2 | ... | y n |
| p | 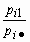
| 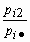
| ... | 
|
И 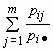 для всех i = 1, 2, …, n. Если условные распределения случайных величин x и h отличаются от их безусловных распределений, то случайные величины x и h зависимы.
для всех i = 1, 2, …, n. Если условные распределения случайных величин x и h отличаются от их безусловных распределений, то случайные величины x и h зависимы.
Например, рассмотрим эксперимент по бросанию одновременно двух костей, с каждым элементарным событием свяжем два числа (Z1, Z2), где Z1 - число очков на первой кости, Z2 - сумма очков на двух костях. Тогда (Z1, Z2) - двумерная случайная величина, поскольку известна вероятность р(хi, хk) пересечения событий, состоящих в том, что Z1 примет значение хi, а Z2 - хk. Для дискретных случайных величин закон распределения задается вероятностями всевозможных комбинаций их значений. Для двумерной величины при небольшом числе возможных значений это удобно представить в виде таблицы, где на пересечении столбца Z1 и строки Z2 стоит вероятность р(z1, z2)
Таки образом, закон распределения двумерной величины Z1, Z2
| Z2 \Z1 | p(Z2) | ||||||
| 1/36 | 1/36 | ||||||
| 1/36 | 1/36 | 1/18 | |||||
| 1/36 | 1/36 | 1/36 | 1/12 | ||||
| 1/36 | 1/36 | 1/36 | 1/36 | 1/19 | |||
| 1/36 | 1/36 | 1/36 | 1/36 | 1/36 | 5/36 | ||
| 1/36 | 1/36 | 1/36 | 1/36 | 1/36 | 1/36 | 1/6 | |
| 1/36 | 1/36 | 1/36 | 1/36 | 1/36 | 5/36 | ||
| 1/36 | 1/36 | 1/36 | 1/36 | 1/9 | |||
| 1/36 | 1/36 | 1/36 | 1/12 | ||||
| 1/36 | 1/36 | 1/18 | |||||
| 1/36 | 1/36 | ||||||
| p(Z1) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Просуммировав все значения р(Z1, Z2) вдоль каждой строки, мы получим вероятности определенных значений Z2, т.е. закон распределения одномерной величины Z2. Аналогично, сумма по столбцам даст закон распределения одномерной величины Z1. Сумма всех чисел в таблице должна быть равна 1.
Пример. Независимые случайные величины X и Y заданы следующими законами распределения:
| X | Y | |||||
| p | 0, 3 | 0, 7 | P | 0, 4 | 0, 6 |
|
|