
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
При плоском движении тела проекции скоростей двух его точек на ось, проходящую через эти точки, равны между собой
|
|
(рис.4.5):  .
.
4.2.3. Теорема о распределении скоростей
Скорости точек тела при плоском движении в каждый момент времени таковы, как если бы, начиная с данного момента времени, плоская фигура стала вращаться вокруг мгновенной оси скоростей с угловой скоростью 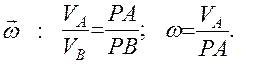
Мгновенный центр скоростей (МЦС) – это такая точка плоской фигуры, скорость которой в данный момент времени равна нулю, при условии, что угловая скорость плоской фигуры не равна нулю.
Ось, проходящая через МЦС перпендикулярно плоской фигуре, называется мгновенной осью скоростей.
Геометрические методы нахождения МЦС приведены на рис. 4.6 (а, б). Мгновенный центр скоростей лежит на пересечении перпендикуляров, восстановленных к векторам скоростей точек.
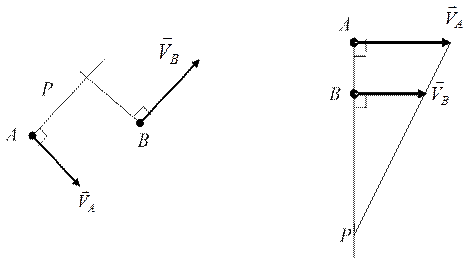
Рис. 4.6, а
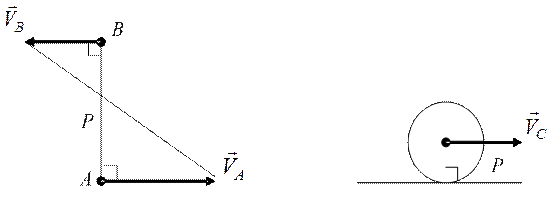
Рис. 4.6, б
Если векторы скоростей двух точек параллельны, направлены в одну сторону и скорости точек равны, то мгновенный центр скоростей плоской фигуры находится в бесконечности, при этом мгновенная угловая скорость тела равна нулю, скорости всех точек тела одинаковы, а ускорения различны. В этом случае тело находится в состоянии мгновенно поступательного движения.
4.2.4. Ускорение точки тела при плоском движении
Ускорение точки при плоском движении тела равно геометрической сумме ускорения полюса и ускорения точки при вращении вокруг полюса:
 ,
,
где  – ускорение точки В при вращении вокруг полюса А.
– ускорение точки В при вращении вокруг полюса А.
4.2.5. К-2. Определение скоростей и ускорений точек многозвенного механизма
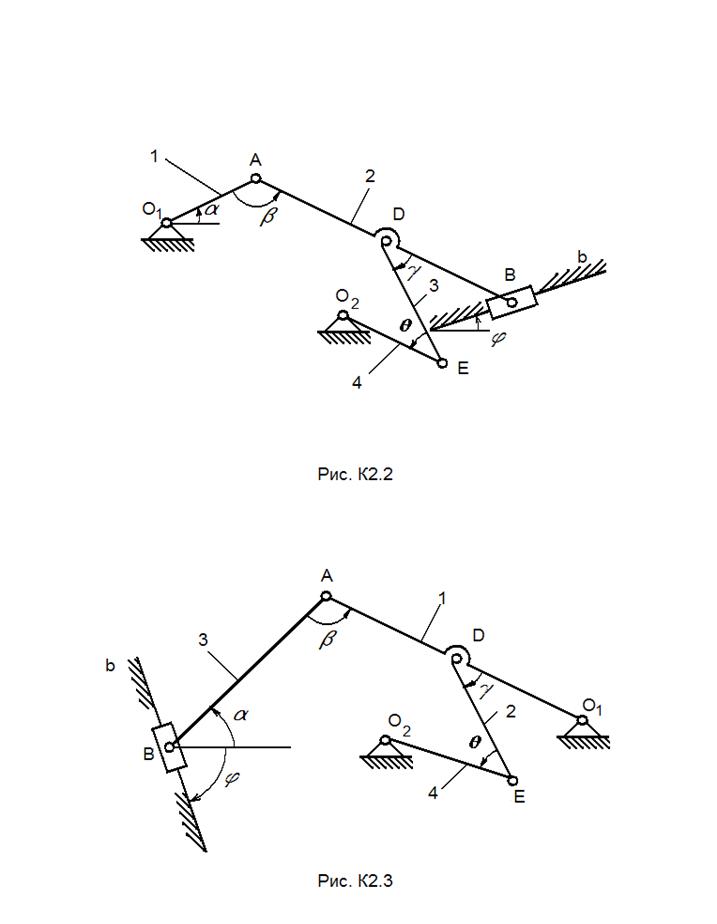
Дано: плоский механизм состоит из 1, 2, 3 и ползунов В и Е (рис. К 2.0 – К 2.1) или из стержней 1, 2, 3, 4 и ползунов В или Е (рис. К 2.2 – К 2.9), соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами; точки D, В и К находятся в серединах соответствующих стержней. Длины стержней равны соответственно: l1=0, 4 м, l2=1, 2 м, l3=1, 4 м, l4=0, 6 м. Положение механизма определяется углами: α, β, γ, φ, θ. Значения этих углов и других заданных величин указаны в таблицах К -2.1 (для рис. К 2.0 – К 2.4) и К 2.2 (для рис. К 2.5 – К 2.9); при этом в табл. К - 2.2 ω 1, ω 4 – величины постоянные.
Определить: скорости и ускорения точек и звеньев плоского механизма, указанные в таблицах в столбцах «Найти».
Указания: построение чертежа следует начинать со стержня, направление которого определяется углом α; дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки.
Заданные угловую скорость и угловое ускорение считать направленными против часовой стрелки, а заданные скорость 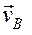 и ускорение
и ускорение 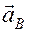 от точки В к b (рис. К 2.0 – К 2.4).
от точки В к b (рис. К 2.0 – К 2.4).
При решении задачи для определения скоростей точек многозвенного механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и теоремой о распределении скоростей. При определении ускорений точек механизма следует исходить из векторного равенства  .
.





4.2.6. Пример К-2
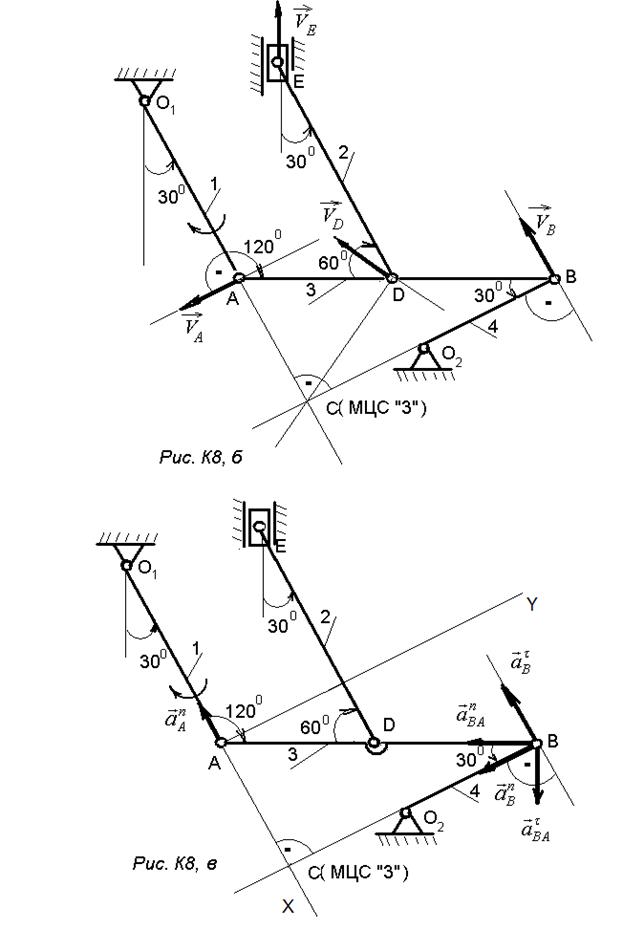
Механизм состоит из стержней 1, 2, 3, 4 и ползуна Е, соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами (рис. К-2).
Дано: l1=0, 4 м, l2=1, 2 м, l3=1, 4 м, l4=0, 6 м, α = 30º, β =60º, γ =30º, φ =0º, θ =120º; AD=DB; ω 1 = 5 рад/c с направлением - по ходу часовой стрелки.
Определить: vB, vE, aB, ω AB, ε AB.
Решение
1. Строим положение механизма в соответствии с заданными углами (рис. К-2, а).
Кинематический анализ:
- звенья О1А и О2В совершают вращательное движение;
- звенья АВ и DE совершают плоскопараллельное движение;
- ползун Е движется поступательно.
2. Для того, чтобы определить скорость точки В, принадлежащей звену АВ, необходимо найти скорость какой-либо точки этого звена. Такой точкой является точка А, принадлежащая одновременно и звену О1А, совершающему вращательное движение с угловой скоростью ω 1 = 5 рад/c по ходу часовой стрелки относительно неподвижного шарнира в точке О1. Точка А движется вместе с кривошипом О1А по окружности радиуса, равного длине звена l1=0, 4 м. Скорость точки А может быть определена выражением: vA = ω 1l1=5·0, 4=2 (м/c). Вектор скорости точки А перпендикулярен звену 1 (О1А) и направлен в сторону вращения кривошипа.
3. На основании теоремы о проекциях скоростей двух точек, принадлежащих телу, совершающему плоское движение, находим направление и модуль скорости точки В:
 ,
,  , vВ = 3, 46 (м/с). Вектор скорости точки В перпендикулярен звену 4 (О2В), поскольку точка В вместе со звеном 4 совершает движение по окружности радиуса l4.
, vВ = 3, 46 (м/с). Вектор скорости точки В перпендикулярен звену 4 (О2В), поскольку точка В вместе со звеном 4 совершает движение по окружности радиуса l4.
Таблица К-2.1 (к рис. К 2.0-К 2.4)
| Номер условия | Углы, град. | Дано | Найти | ||||||||||
| α | β | γ | φ | θ | ω 1 рад/c | ε 1 рад/c2 | V В м/c | aВ м/c2 | V точек | ω звена | a точки | ε звена | |
| - | - | В, Е | АВ | В | АВ | ||||||||
| - | - | А, D | DE | A | AB | ||||||||
| - | - | B, E | DE | B | AB | ||||||||
| - | - | A, E | AB | A | AB | ||||||||
| - | - | B, E | DE | B | AB | ||||||||
| - | - | D, E | DE | A | AB | ||||||||
| - | - | B, E | AB | B | АВ | ||||||||
| - | - | A, E | DE | A | AB | ||||||||
| - | - | B, E | AB | B | AB | ||||||||
| - | - | D, E | AB | A | AB |
Таблица К-2.2 (к рис. К 2.5-К 2.9)
| Номер условия | Углы, град. | Дано | Найти | ||||||||
| α | β | γ | φ | θ | ω 1 рад/c | ω 4 рад/c | V точек | ω звена | a точки | ε звена | |
| - | В, K | DE | В | АВ | |||||||
| - | А, E | DE | A | AB | |||||||
| - | B, K | AB | B | AB | |||||||
| - | A, E | DE | A | AB | |||||||
| - | D, K | AB | B | AB | |||||||
| - | A, E | AB | A | AB | |||||||
| - | B, E | DE | B | АВ | |||||||
| - | A, K | DE | A | AB | |||||||
| - | D, E | AB | B | AB | |||||||
| - | A, K | AB | A | AB |
4. Для определения линии действия вектора скорости точки D построим мгновенный центр скоростей (МЦС) звена АВ: МЦСАВ(3) – точка С, лежащая на пересечении перпендикуляров, восстановленных из точек А и В к векторам их скоростей  . Вектор скорости точки D перпендикулярен отрезку DС – расстояние от точки D до мгновенного центра скоростей звена АВ, которому точка D принадлежит.
. Вектор скорости точки D перпендикулярен отрезку DС – расстояние от точки D до мгновенного центра скоростей звена АВ, которому точка D принадлежит.
5. Определяем угловую скорость звена АВ: ω АВ(3)= vA / АС, где АС - катет, лежащий против угла равного 300, АС = 0, 5·АВ=0, 7 (м); ω АВ(3)= 2 / 0, 7=2, 86 (рад/с).
6. Определяем линию действия, направление и модуль вектора скорости ползуна, принятого за материальную точку Е.
Линия действия вектора 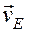 параллельна направляющим ползуна (совпадает с осью ползуна), который движется поступательно. Направление вектора
параллельна направляющим ползуна (совпадает с осью ползуна), который движется поступательно. Направление вектора 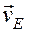 и его модуль находим, используя теорему о проекциях скоростей двух точек, принадлежащих одному и тому же телу, совершающему плоское движение:
и его модуль находим, используя теорему о проекциях скоростей двух точек, принадлежащих одному и тому же телу, совершающему плоское движение:
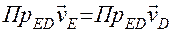 ,
, 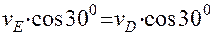 , vE = vD= vA= 2 (м/с).
, vE = vD= vA= 2 (м/с).
7. Определяем 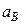 . Точка В принадлежит звену АВ. Чтобы найти её ускорение, необходимо знать ускорение какой-нибудь точки этого звена (полюса) и траекторию точки В. Точка В движется по окружности вместе с кривошипом О2В, и поэтому направление вектора
. Точка В принадлежит звену АВ. Чтобы найти её ускорение, необходимо знать ускорение какой-нибудь точки этого звена (полюса) и траекторию точки В. Точка В движется по окружности вместе с кривошипом О2В, и поэтому направление вектора 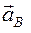 заранее известно.
заранее известно.
Ускорение точки В при плоском движении тела равно геометрической сумме ускорения полюса А и ускорения точки В при вращении вокруг полюса А:
 .
.
Разложив векторы ускорений на составляющие по естественным осям, получим следующее векторное равенство:
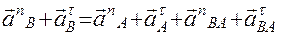 .
.
Векторы ускорений будут направлены следующим образом: вектор  – по радиусу О2В к центру О2 окружности; вектор
– по радиусу О2В к центру О2 окружности; вектор  – перпендикулярно О2В в любую сторону; вектор
– перпендикулярно О2В в любую сторону; вектор 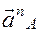 – по радиусу О1А к центру О1 вращения; вектор
– по радиусу О1А к центру О1 вращения; вектор 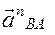 – по радиусу ВА к центру А вращения; вектор
– по радиусу ВА к центру А вращения; вектор  – перпендикулярно ВА в любую сторону. Поскольку по условию задачи точка А, принадлежащая звену О1А, движется равномерно, то её касательное ускорение равно 0
– перпендикулярно ВА в любую сторону. Поскольку по условию задачи точка А, принадлежащая звену О1А, движется равномерно, то её касательное ускорение равно 0  , и поэтому на чертеже вектор
, и поэтому на чертеже вектор  не изображаем.
не изображаем.
8. Спроецируем обе части уравнения на координатные оси X и Y:


9. Определяем  ,
, 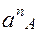 ,
,  :
:

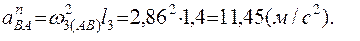
10. Подставляя известные значения в уравнения, полученные при проецировании векторной суммы, находим  и
и  :
:  = -1, 66 (м/с2),
= -1, 66 (м/с2),
 = 20, 07(м/с2). Знак «-» означает, что вектор касательного ускорения точки В фактически имеет направление противоположное выбранному в ходе решения задачи.
= 20, 07(м/с2). Знак «-» означает, что вектор касательного ускорения точки В фактически имеет направление противоположное выбранному в ходе решения задачи.
11. Находим полное ускорение точки В: 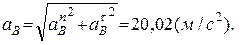
12. Угловое ускорение звена АВ определяется выражением:
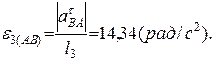
Ответ: vB=3, 46(м/с), vE =2(м/с), aB =20, 02(м/с), ω AB=2, 86(м/с), ε AB=14, 34(рад/с2).
4.3. Сложное движение точки
Движение точки относительно системы координат, принимаемой за неподвижную, называют сложным, если его можно представить как движение точки относительно подвижной системы координат и движение точки вместе с подвижной системой относительно неподвижной.
4.3.1. Основные определения и правила в теории сложного движения точки
Абсолютным движением, скоростью, ускорением точки называют её движение, скорость, ускорение относительно неподвижной системы координат.
Абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей  .
.
Абсолютное ускорение точки равно геометрической сумме относительного, переносного ускорений и ускорения Кориолиса 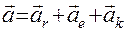 .
.
Относительным движением, скоростью 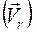 , ускорением
, ускорением 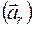 точки называют её движение, скорость, ускорение относительно подвижной системы координат.
точки называют её движение, скорость, ускорение относительно подвижной системы координат.
Переносным движением называют движение подвижной системы координат относительно неподвижной.
Переносной скоростью 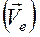 точки называют её скорость в переносном движении.
точки называют её скорость в переносном движении.
Переносным ускорением точки  называют её ускорение в переносном движении.
называют её ускорение в переносном движении.
Чтобы вычислить относительную скорость (относительное ускорение), надо мысленно остановить подвижную систему координат, не останавливая движения точки, и вычислить скорость (ускорение) точки относительно мысленно остановленной системы координат.
Чтобы вычислить переносную скорость (переносное ускорение), надо мысленно остановить точку в подвижной системе координат и вычислить
скорость (ускорение) того места подвижной системы координат, с которым совпадает точка в данный момент времени.
Ускорение Кориолиса точки есть удвоенное векторное произведение переносной угловой скорости на относительную скорость точки 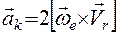 .
.
Вектор ускорения Кориолиса перпендикулярен плоскости, которой принадлежат векторы угловой переносной и относительной скорости точки, и направлен в ту сторону, откуда кратчайший поворот от вектора  к вектору
к вектору  на наименьший угол виден происходящим против хода часовой стрелки. Если векторы не лежат в одной плоскости, следует мысленно перенести вектор угловой переносной скорости параллельно самому себе в заданную точку и применить сформулированное выше правило.
на наименьший угол виден происходящим против хода часовой стрелки. Если векторы не лежат в одной плоскости, следует мысленно перенести вектор угловой переносной скорости параллельно самому себе в заданную точку и применить сформулированное выше правило.
Иногда нахождение направления ускорения Кориолиса облегчает применение правила Жуковского: спроецировать вектор относительной скорости на плоскость, перпендикулярную вектору угловой переносной скорости, и повернуть полученную проекцию в этой плоскости вокруг известной точки на угол 900 в сторону переносного вращения.
4.3.2. К-3. Определение абсолютной скорости и абсолютного ускорения точки
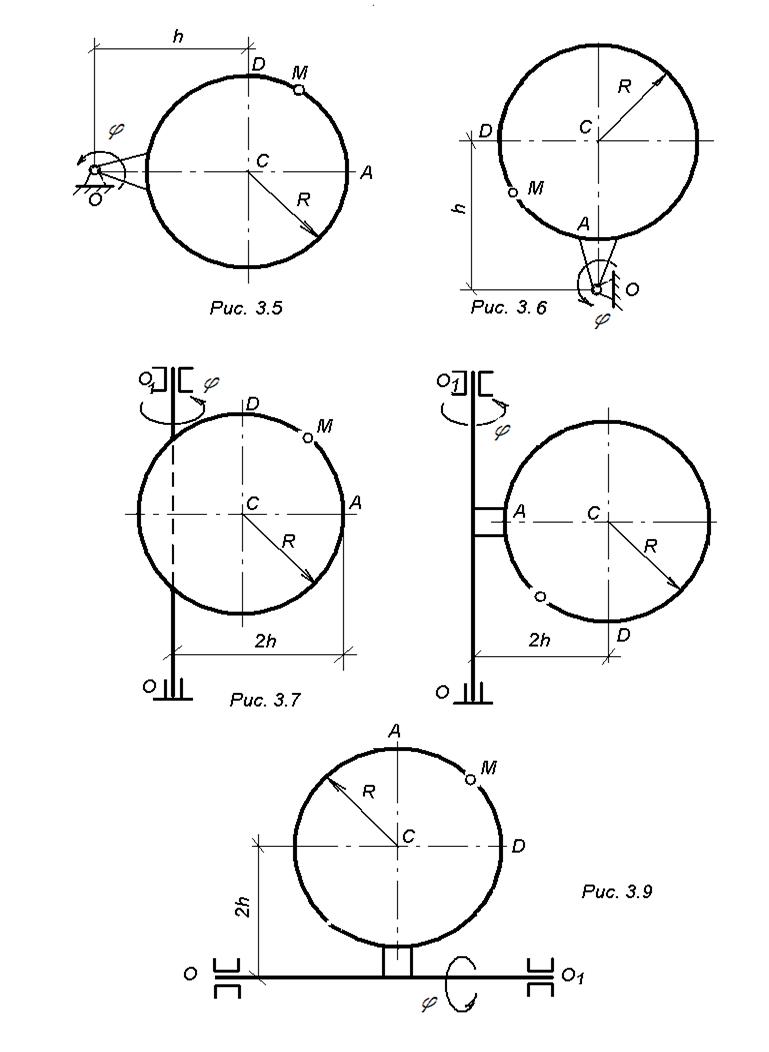
Дано: прямоугольная пластина (рис. К 3.0 – К 3.4) или круглая пластина радиуса R = 60 см (рис. К 3.5 – К 3.9) вращается вокруг неподвижной оси по закону φ =f1(t), заданному в табл. К - 3. Положительное направление отсчета угла показано на рисунках дуговой стрелкой. На рис. 0, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4.7, 8, 9 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. К3.0 - К3.4) или по окружности радиуса R (рис. К3.5 – К3.9) движется точка М; закон ее относительного движения, то есть зависимость s=AM=f2(t) (s - в сантиметрах, t – в секундах), задан в таблице отдельно для рис. К3.0 - К3.4 и для рис. К3.5 – К3.9; там же даны размеры а и h. На рисунках точка М показана в положении, при котором s=AM ›0 (при s‹0 точка М находится по другую сторону от точки А).
Определить: абсолютную скорость и абсолютное ускорение точки М в момент времени t1 =1 c.
Указания: для решения задачи необходимо воспользоваться теоремами о сложении скоростей и ускорений. Прежде чем производить расчеты, следует определить, где находится точка на пластине в момент времени t1 =1 c и изобразить точку именно в этом положении.
4.3.3. Пример К– 3
По пластине вдоль прямой BD движется точка М; пластина вращается вокруг оси, перпендикулярной плоскости пластины, по известному закону
(рис. К-3).
Дано: φ =2t3 –t2 (рад); s=AM=18sin(π t/4) см; t1=2/3 с; а=25 см.
Определить: для момента времени t1 абсолютную скорость и абсолютное ускорение.
Таблица К-3
| Номер рисунка | Для всех рисунков φ =f1(t) | Для рис. К 3.0-К 3.4 | Для рис. К 3.5-К 3.9 | ||
| а, см | S=AM=f2(t) | h | S=AM=f2(t) | ||
| 4(t2-t) | 50(3t-t2)-64 | R | (π R/3)·(4t2-2t3) | ||
| 3t2-8t | 40(3t2-t4)-32 | 4R/3 | (π R/2)·(2t2-t3) | ||
| 6t3-12t2 | 80(t2-t)+40 | R | (π R/3)·(2t2-1) | ||
| t2-2t3 | 60(t4-3t2)+56 | R | (π R/3)·(t4-3t2) | ||
| 10t2-5t3 | 80(2t2-t3)-48 | R | (π R/6)·(3t-t2) | ||
| 2(t2-t) | 60(t3-2t2) | R | (π R/3)·(t3-2t) | ||
| 5t-4t2 | 40(t2-3t)+32 | 3R/4 | (π R/2)·(t3-2t2) | ||
| 15t-3t3 | 60(t-t3)+24 | R | (π R/6)·(t-5t2) | ||
| 2t3-11t | 50(t3-t)-30 | R | (π R/3)·(3t2-t) | ||
| 6t2-3t3 | 40(t-2t3)-40 | 4R/3 | (π R/2)·(t-2t2) |


|
|