Со смешанными граничными условиями. Решение задач МКЭ заключается в минимизации некоторого вариационного функционала

Решение задач МКЭ заключается в минимизации некоторого вариационного функционала. Вариационная формулировка краевой задачи пластического деформирования в форме Лагранжа запишется в виде

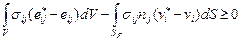, (4.30)

где V – объем тела; n_j – направляющие косинусы единичного вектора нормали n к поверхности S_F, на которой задана нагрузка. Индексом (*) отмечены кинематически возможные скорости и соответствующий им тензор скоростей деформаций. Знак равенства в (4.30) соответствует полю действительных скоростей. При численном решении МКЭ вместо вариационного неравенства (4.30) используется эквивалентная экстремальная формулировка. В этом случае рассматривается вариационный функционал

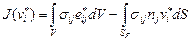. (4.31)

Действительное поле скоростей соответствует минимуму функционала (4.31).

Поставленная задача с трением на контактной поверхности инструмента S_c приводит к вариационному неравенству [92]

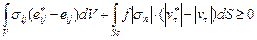. (4.32)

В интеграл по S_c входит напряжение | s_n |, которое является неизвестной величиной, и его нельзя представить в виде разности интегралов, один из которых определяется полем допустимых скоростей, а второй - полем действительных скоростей. Неравенство (4.32) является квазивариационным и не допускает экстремальную формулировку. В этом случае используется итерационный процесс замены квазивариационного неравенства последовательностью вариационных неравенств, для которых существует эквивалентная экстремальная формулировка [22, 86, 92]. На первом шаге принимается 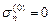и рассматривается задача без учета трения. Из решения этой задачи определяется нормальное напряжение на S_c, которое принимается в качестве первого приближения 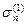. Затем при решается неравенство (4.39) и т. д. На k -том шаге итерационного процесса рассматривается решение вариационного неравенства

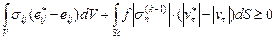. (4.33)

Тогда вариационный функционал экстремальной задачи запишется в виде

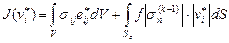. (4.34)

Минимуму функционала (4.34) соответствует действительное поле скоростей v (x, t). Так как сила трения Прандтля зависит от плотности r материала оболочки, которая является неизвестной величиной, то описанный итерационный процесс применяется и в случае действия закона трения Прандтля. Отметим, что теоретически сходимость описанного метода решения задач с трением не доказана, но в некоторых случаях решение получается за конечное число итераций [86, 92].

Конечно-элементная аппроксимация функционала (4.34) для сред с различной реологией достаточно подробно рассмотрена в обширной литературе по теории и практическому применению МКЭ [65, 130, 171, 196]. В результате аппроксимации интегрирование заменяется суммированием по конечным элементам, и минимизация функционала (4.34) приводит к системе алгебраических уравнений вида

[ K ]× { v } = { F }, (4.35)

где [ K ] – глобальная матрица жесткости; { v } – вектор-столбец узловых скоростей; { F } – вектор-столбец узловых усилий.

Вследствие нестационарности уравнения неразрывности (4.19) для уплотняемых тел имеет место неустановившееся течение. Краевая задача неустановившегося движения решается методом пошагового нагружения по времени, что эквивалентно решению дифференциального уравнения (4.19) методом конечных разностей.

Выполнение заданных кинематических граничных условий (4.25) осуществляется путем модификации глобальной матрицы жесткости [ K ]. При этом диагональный элемент матрицы [ K ], соответствующий заданной скорости, умножается на заведомо большое число, например 10⁸. Соответствующий компонент вектора { F } модифицируется по правилу

, (4.36)

где m – индекс направления, в котором скорость точки равна заданной скорости v_m.

В вектор узловых усилий { F } входят поверхностные нагрузки. В рассматриваемой задаче поверхностными нагрузками являются узловые силы внешнего трения оболочки 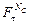в граничных узлах N_с на S_c. Величина узловых сил 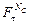определяется через нормальные силы : 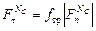. Так как силы неизвестны, то используется итерационный процесс, рассмотренный выше.

Соотношения Коши и определяющие соотношения внутри конечного элемента выражаются уравнениями

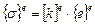; , (4.37)

где [ В ] – матрица дифференцирования; [ k ] ^e – матрица жесткости конечного элемента.

В рамках пошагового метода решения задач пластического деформирования система уравнений (4.35) решается для каждого временного шага. Для текущего шага по времени после нахождения вектора узловых скоростей { v } определяются перемещения и новые координаты узлов сетки конечных элементов. На каждом следующем временном шаге для новой конфигурации конечно-элементной сетки вновь рассчитываются локальная и глобальная [ K ] матрицы жесткости.

В МКЭ важным моментом является выбор формы конечного элемента и способа аппроксимации функции – линейная или нелинейная аппроксимация. Для сжимаемых тел нелинейная аппроксимация поля скоростей приводит к неоднородному полю скоростей деформаций и плотности в объеме конечного элемента. В связи с этим необходимо решать дифференциальное уравнение неразрывности (4.19) для каждого конечного элемента, поэтому был выбран осесимметричный конечный элемент с треугольным сечением и линейной аппроксимацией скоростей. В этом случае скорость изменения объема конечного элемента, равная , является постоянной величиной, и дифференциальное уравнение неразрывности превращается в алгебраический закон сохранения массы.

Матрица дифференцирования [ B ] в первом уравнении (4.37) определяется видом аппроксимации скоростей по объему V^е конечного элемента. Матрица жесткости конечного элемента [ k ] ^e имеет вид

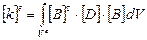. (4.38)

Верхний индекс ² т² в выражении (4.38) означает операцию транспонирования матрицы. Матрица [ D ] отражает реологические свойства материала и формируется на основании определяющих соотношений (4.21) и (4.22):

. (4.39)

Множитель перед матрицей в (4.39) равен

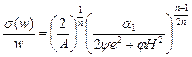(4.40)

для нелинейно-вязких продуктов синтеза и

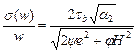(4.41)

для сыпучей оболочки.

Элементы матрицы [ B ] вычисляются по известным зависимостям для осесимметричных конечных элементов треугольного сечения [171].

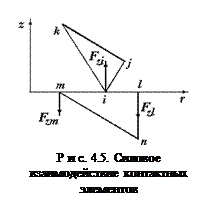
Как отмечалось выше, в модели принято, что контактное взаимодействие заготовки и оболочки происходит в отсутствии сил трения. В дискретизированном на конечные элементы объекте контактное взаимодействие осуществляется через соответствующие узлы. Учитывая, что скорости внутри элемента изменяются линейно, условие совместности нормальных компонент скоростей на верхней опорной плоскости заготовки при осесимметричном течении
(рис. 4.5) запишется в виде

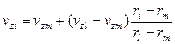. (4.42)

Касательные компоненты скоростей заготовки и оболочки на их границе независимы друг от друга. В МКЭ силы могут быть приложены только в узлах, поэтому контактная сила, возникающая в узле контакта i заготовки, заменяется эквивалентными силами, которые приложены в узлах l и m. Эти эквивалентные силы выражаются через величину контактной силы в
i -том узле оболочки аналогично уравнению (4.42). Тогда силы контактного взаимодействия на опорных поверхностях оболочки и заготовки будут связаны соотношениями [126]

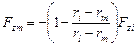; . (4.43)

По аналогии для цилиндрической контактной поверхности будем иметь

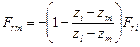; . (4.44)

По отношению к оболочке и заготовке контактные силы являются внешними, и величина их неизвестна. В итоге, наряду с неизвестными скоростями узлов, появляются новые неизвестные – силы контактного взаимодействия оболочки и заготовки. Одновременно к системе алгебраических уравнений (4.35) добавляется столько уравнений совместности скоростей (4.42), сколько контактных узлов имеют заготовка и оболочка. При решении в векторе узловых скоростей { v } системы (4.35) за неизвестные принимались нормальные компоненты скоростей контактных узлов оболочки, а нормальные компоненты скоростей контактных узлов заготовки находились по уравнениям совместности (4.42). Для удовлетворения условиям совместности (4.42) - (4.44) производилась вторая модификация глобальной матрицы жесткости [ K ]. В результате этой модификации нарушается симметричность матрицы [ K ]. В классической постановке МКЭ глобальная матрица жесткости является симметричной и ленточной. Соответственно разработаны специальные производительные методы решения диагональных симметричных систем линейных алгебраических уравнений. В нашем случае контактное взаимодействие оболочки и заготовки приводит к несимметричной ленточной матрице с окаймлением [126], поэтому решение получаемой системы линейных алгебраических уравнений производилось методом Гаусса.

Нелинейный характер определяющих соотношений (4.21) и (4.22) обусловливает физическую нелинейность поставленной краевой задачи и ее дискретного аналога в форме (4.35). При решении на ЭВМ нелинейную краевую задачу сводят к последовательности линейных краевых задач. Линеаризация уравнений жесткопластического течения (для оболочки) и нелинейно-вязкого течения (продукты синтеза) выполнялась методом гидродинамических приближений (методом переменной вязкости). Определяющие соотношения (4.21) и (4.22) запишем в виде

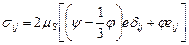. (4.45)

Соотношения (4.45) по форме совпадают с определяющими соотношениями теории линейно-вязкой сжимаемой жидкости, если под m_S = s (w)/2 w понимать коэффициент вязкости. В соотношениях (4.45) m _S не является постоянной величиной, а зависит от искомых параметров течения: полей плотности r (x, t) и скорости v (x, t). Поскольку функция m_S (r, v) заранее неизвестна, то используется итерационный процесс последовательного уточнения m_S (r, v). Тем самым метод переменной вязкости аналогичен известному методу переменных параметров упругости. Таким образом, на каждом временном шаге нагружения при решении системы нелинейных алгебраических уравнений (4.35) реализуются два итерационных процесса. Основной итерационный процесс связан с определением сил контактного трения оболочки. Внутри каждой итерации основного процесса выполняется второй итерационный процесс по решению физически нелинейной задачи пластического течения.