Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Характеристики распределений

Лекция №9. Статистические методы при построении математических моделей.

Законы распределения параметров системы

Для построения адекватной математической модели объекта необ­ходимо знать законы распределения параметров, характеризую­щих его функционирование. При этом под законом распределения понимают связь между возможными значениями случайной ве­личины и соответствующими им вероятностями. Эта связь выра­жается интегральной функцией распределения показывающей вероятность того, что случайная величина Х не превышает некоторого числа х.

Р (х) = Р (X < = х}, (9.1)

Закон распределения конкретного параметра определяетется природой контролируемой величины. Обычно функцию распределения для описания изменения той или иной характеристики системы выбирают на основе имеющихся представлений о механизме рассматриваемого явления. Затем на основании имеющихся экспериментальных или статистических данных делают оценка параметров распределения и в заключение осуществляют статистичсскую проверку гипотезы об адекватности выбранной модели распределения реальному распределению. Когда нет достаточно надежных теоретических оснований для выбора статистической модели распределения, аппроксимирующее распределение выбирают по данным оценки параметров распределения с последующей проверкой адекватности. Вид функции распределения предпочтительнее выбирать на основе представлений о физической природе явления, так как исключаются возможные большие погрешности при распространении найденных закономерности за пределы изученного интервала варьирования случайной величины.

Характеристики распределений

Математическое ожидание или среднее значение случайной величины

МХ = v_x. (9.2)

В случае непрерывной случайной величины

МХ = 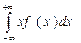(9.3)

где f(х) - плотность распределения величины х.

Если же х - дискретная случайная величина, то

МХ= 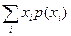(9.4)

где р(х_i) — вероятность появления i-того значения величины х.

Медиана - значение случайной величины, отвечающее сере­дине упорядоченного по величине ряда значений переменной. В случае непрерывной случайной величины медианой является такая точка z, при которой

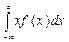= 0, 5 (9.5)

а в случае дискретной переменной

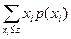= 0, 5. (9.6)

Если общее число n значений дискретной случайной величины нечетно, то медиана равна значению случайной величины с ин­дексом i=(n+1)/2. При четном n медиана равна

½ (x_n/2 + x_(n/2+1)) (9.7)

Мода - значение случайной величины, отвечающее макси­мальной плотности вероятности f(х) в случае непрерывной слу­чайной величины, или значение случайной величины, имеющей максимальную вероятность в том случае, когда случайная вели­чина дискретна.

Кроме характеристик положения центра, пользуются еще рядом других характеристик, описывающих рассеяние, симме­трию и островершинность распределения. Эти характеристики можно, представить с помощью моментов распределения. На практике чаще всего применяют моменты двух видов: начальные и центральные.

Начальным моментом s -ного порядка дискретной случайной величины Х называют сумму вида: v_s= 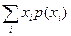(9.8)

а в случае непрерывной случайной величины он равен

v_s= 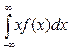(9.9)

Таким образом, начальный момент s-ного порядка есть мате­матическое ожидание s-ной степени случайной величины X:

v_s = МХ^s. (9.10)

Начальный момент первого порядка случайной величины Х равен математическому ожиданию v_x.

Центральным моментом 5-ного порядка случайной величины Х называют математическое ожидание s-ной степени отклонения случайной величины Х от ее математического ожидания v_x

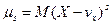(9.11)

Для дискретной случайной величины s-ный центральный момент равен

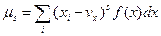(9.12)

а для непрерывной - интегралу

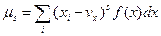(9.13)

Центральный момент второго порядка 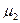- диспер­сия, служит в качестве меры рассеяния:

DX = 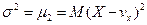(9.14)

Корень квадратный из дисперсии- средне квадратическое отклонение или стандарт.

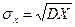(9.15)

В качестве относительной характеристики рассеяния исполь­зуют коэффициент вариации - отношение среднего квадратического отклонения к математическому ожида­нию случайной величины

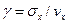(9.16)

Центральный момент третьего порядка 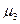используется для числового измерения асимметрии распределения. Если распреде­ление симметрично, то 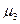= 0. Если правое плечо распреде­ления длиннее левого, то величина 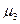положительная, если же, наоборот, левое плечо длиннее правого, то величина 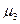отрица­тельна. Чтобы иметь дело с безразмерной величиной 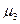делят на 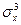. Полученный показатель называют коэффициентом асимметрии (skewness)

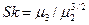(9.17)

В качестве характеристики островершинности служит коэф­фициент эксцесса (excess) 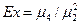(9.18)