
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейная зависимость и независимость векторов
|
|
Определение 1. Множество элементов произвольной природы называется векторным пространством или линейным векторным пространством, если для этих элементов введены операции сложения и умножения на действительное число, причем для этих операций справедливы 8 свойств, указанных для операций с геометрическими векторами.
Пусть заданы векторы 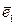 ,
,  , …,
, …, 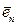 векторного пространства и числа
векторного пространства и числа 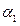 ,
, 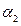 , …,
, …,  . Величина
. Величина 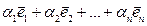 (1)
(1)
называется линейной комбинацией заданных векторов  ,
,  , …,
, …, 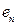 . При этом числа
. При этом числа 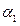 ,
, 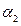 , …,
, …,  называются коэффициентами линейной комбинации (1). Очевидно, что линейная комбинация векторов равна
называются коэффициентами линейной комбинации (1). Очевидно, что линейная комбинация векторов равна 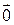 (нулевому вектору), если все коэффициенты линейной комбинации равны 0. Может ли линейная комбинация векторов быть равной 0 при других обстоятельствах?
(нулевому вектору), если все коэффициенты линейной комбинации равны 0. Может ли линейная комбинация векторов быть равной 0 при других обстоятельствах?
Определение 1. Система векторов 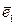 ,
,  , …,
, …, 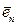 называется линейно независимой системой векторов, если из равенства
называется линейно независимой системой векторов, если из равенства 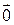 ее линейной комбинации следует, что все коэффициенты этой линейной комбинации равны 0.
ее линейной комбинации следует, что все коэффициенты этой линейной комбинации равны 0.
Если не выполнены условия определения 1, то система векторов называется линейно зависимой системой векторов. Система векторов линейно зависима тогда и только тогда, когда один из векторов системы равен линейной комбинации остальных векторов этой системы.
Геометрическими векторы называются коллинеарными векторами, если они параллельны одной прямой.
Геометрическими векторы называются компланарными векторами, если они параллельны одной плоскости.
Теорема 1. Любые 2 не коллинеарных вектора на плоскости линейно независимы, причем любой третий вектор является их линейной комбинацией.
Теорема 2. Любые 3 не компланарных вектора на плоскости линейно независимы, причем любой четвертый вектор является их линейной комбинацией.
Доказательство теорем 1 и 2 проводится в школьном курсе и приведено на лекции.
Определение 2. Линейно независимая система векторов линейного векторного пространства 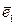 ,
,  , …,
, …, 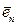 называется базисом этого векторного пространства, если каждый его вектор является линейной комбинацией векторов
называется базисом этого векторного пространства, если каждый его вектор является линейной комбинацией векторов 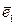 ,
,  , …,
, …, 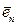 . При этом коэффициенты этой линейной комбинации определяются однозначно и называются координатами вектора в этом базисе.
. При этом коэффициенты этой линейной комбинации определяются однозначно и называются координатами вектора в этом базисе.
Следовательно, любые 2 не коллинеарных вектора  и
и 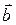 на плоскости образуют базис. Это означает, что для произвольного вектора
на плоскости образуют базис. Это означает, что для произвольного вектора 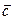 существуют числа
существуют числа 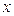 и
и 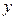 такие, что
такие, что  . Числа
. Числа 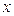 и
и 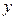 определяются однозначно и называются координатами вектора
определяются однозначно и называются координатами вектора 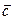 в базисе
в базисе  ,
, 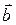 .
.
Аналогично любые 3 не компланарных вектора  ,
, 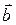 и
и 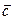 в пространстве образуют базис. Это означает, что для произвольного вектора
в пространстве образуют базис. Это означает, что для произвольного вектора 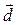 существуют числа
существуют числа 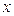 ,
, 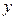 ,
, 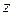 такие, что
такие, что 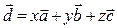 . Числа
. Числа 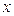 ,
, 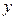 ,
, 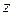 определяются однозначно и называются координатами вектора
определяются однозначно и называются координатами вектора 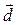 в базисе
в базисе  ,
, 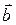 ,
, 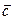 . Давайте в этом случае проверим, что коэффициенты разложения вектора по базису, т. е. координаты вектора определяются однозначно. Пусть справедливы 2 равенства:
. Давайте в этом случае проверим, что коэффициенты разложения вектора по базису, т. е. координаты вектора определяются однозначно. Пусть справедливы 2 равенства:  и
и  . Их разность дает соотношение
. Их разность дает соотношение  . Однако векторы базиса
. Однако векторы базиса  ,
, 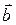 ,
, 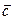 линейно независимы, и из равенства
линейно независимы, и из равенства 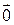 их линейной комбинации следует, что все коэффициенты этой линейной комбинации равны 0, т. е.
их линейной комбинации следует, что все коэффициенты этой линейной комбинации равны 0, т. е. 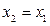 ,
, 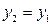 ,
,  . Следовательно, 2 написанных разложения являются одним и тем же разложением вектора по базису.
. Следовательно, 2 написанных разложения являются одним и тем же разложением вектора по базису.
Заметим, что в рассмотренных примерах число векторов базиса не зависит от выбора базиса. Это число называется размерностью векторного пространства. Плоскость является линейным пространством размерности 2, а обычное пространство имеет размерность 3.
|
|