Серпімді кернеу.

1.Деформацияланғ ан дененің тү рлі бір-бірімен шекаралас бө ліктері ө зара ә серлеседі. Қ андай да бір деформацияланғ ан денені немесе ортаны қ арастырайық. Денені ойша 2 бө лікке бө лейік: АВ жазық тығ ында шектесетін дене І жә не дене ІІ.Дене І деформацияланатындық тан ол белгілі кү шпен дене ІІ –ге ә сер етеді.Тура осындай себептен дене ІІ –де сондай, бірақ қ арама-қ арсы кү шпен дене І-ге ә сер етеді. Бірақ пайда болатын деформация- ны АВ қ имасына ә сер ететін кү штердің қ осындысын білу жеткіліксіз.Сонымен қ атар бұ л кү штер осы қ имада қ алай таралатыны кө рсетілуі тиіс. АВ жазық тығ ынан шексіз кіші dS ауданын бө ліп алайық. dF-дене ІІ дене І –ге осы ауданда ә сер ететін кү ш болсын. Бірлік ауданғ а тура елетін кү ш, яғ ни 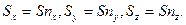кернеу деп аталады. Бұ л жағ дайда АВжазық тығ ының деғ не І-дің шегарасында ә сер ететін кернеу деп аталады. Осы нү ктеде дене ІІ шегарасында ә сер ететін кернеу тура осындай, бірақ бағ ыты қ арама –қ арсы болады.

197-сурет

2.dS ауданының бағ ытын оғ ан нормаль жү ргізу арқ ылы таң дауғ а болады.Нормальді dF кү ші ә сер ететін дене жазық тығ ының сыртына қ арай жү ргіземіз. Нормальдің бірлік векторын n, ал сә йкес кернеуді деп белгілейміз. 1-ші сурет бойынша =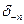

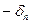
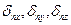-декарт координатасында

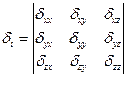— кернеулік тензоры

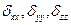—нормальдық элементтер, қ алғ андары жанама элементтер.

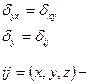
-симетриялық тензор

Сонда 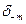дене І-мен шекаралас дене ІІ-нің АВ жазық тығ ындағ ы кернеу болады. Ә сер менн қ арсы ә сер тең болғ андық тан =

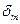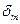векторын n нормаль борйымен жә не dS ауданына жанма бойында жататын қ ұ раушыларғ а жіктеуге болады. Оның біріншісі нормаль, ал екіншісі – тангенциал қ ұ раушы деп аталады. Кез келген вектор сияқ ты 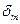кернеуін Х, У, Z координаттар системасының осьтері бойынша сипаттауғ а болады. Бұ л қ ұ раушыларды сә йкесінше 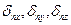болады.Бірінші индекс дене бетінің сыртқ ы нормальдің бағ ытын, ал екіншісі - 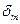векторы проекцияланатын осьтің бағ ытын кө рсетеді. Сә йкесінше сыртқ ы нормалі х осінің бағ ытына аудандағ ы параллель бағ ытты кө рсетеді.

3. Кернеудің опртаның бір нү ктесіндегі бағ ытын анық тау ү шін осы нү кте арқ ылы ө тетін ө зара перпендикуляр аудандағ ы бағ ыттарды анық тасақ болғ аны. Бұ л тыныштық та тұ рғ ан ортағ а да, белгілі ү деумен қ озғ алып бара жатқ ан ортағ а орындалады. Мұ ны дә лелдеу ү шін қ арастырылып отырғ ан нү ктеге координаттар басын орналастырамыз жә не одан шексіз кіші ОАВС кө лемді координаттар жазық тық тарымен шектесетін жә не АВС жазық тығ ымен қ иылып ө тетін элемент бө ліп алайық.

2-ші сурет бойынша тұ тас дененің формасы кө рсетілген.Оның тө рт беті бар. Егер АВС бетіне 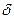-кернеу ә сер етсе онда бұ л тұ тас кө лемнің қ озғ алысы мынадай

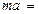f+ -

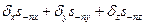
f-тұ тас ортағ а ә сар етуші массалық кү ш.

Массалық кү ш (ауырлық) тағ ы басқ а концервативті кү штер болуы мү мкін.

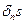-АВС бетіне 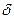нормаль бағ ытымен бағ ыттас.

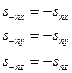
а=0

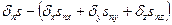f=0

=0

n-АВС 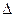-ның жазық тығ ына жү ргізілген сыртқ ы жанамасы. Сонда АСВ бетіндегі бө ліп алынғ ан элементі сыртқ ы ортадан ә сер ететін кү ші 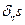болады, мұ ндағ ы S беттің ауданы. Сә йкесінше ү ш бү йір бетке ә сер ететін кү штер

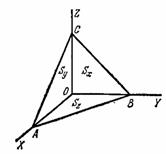198-сурет.

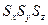болады. Мұ ндағ ы осы беттердің ауданы. Бұ л кү штерден басқ а осы бө ліп алынғ ан элементке массалық немесе кө лемдік кү штер ә сер етуі мү мкін.Мысалы, ауырлық кү ші. Барлық ә сер етуші кү штердің қ орытқ ы кү шін деп белгілейік.

кү ші бө ліп алынғ ан элементтің кө леміне пропорционал. Егер элемент массасы m ал ү деуі 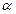болса, онда

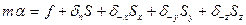Бұ л жерде тү рлендірулер жү ргізейік, OABC элементін нү ктеге дейін кішірейтейік. Мұ ндай жағ дайда ө рнектің жә не f мү шелерін алып тастауғ а болады. Олар OABC элементінің кө леміне пропорционал. Ө рнектің басқ а мү шелерімен салыстырғ анды олар жоғ ары дә режеде шексіз кіші болады. S ауданның координата жазық тығ ына проекциясы былай анық талады: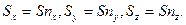

Сонымен қ атар 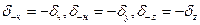болатындығ ын ескереміз. Сонда нә тижесінде мынаны аламыз: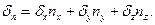

X, Y, Z ө з қ алауымыз бойынша таң дауымызғ а болатындық тан теорема дә лелденді.

Осылайша серпімді деформацияланғ ан дененің кернеуін векторлары арқ ылы немесе олардың тоғ ыз проекциялары тү сіндіруге болады:

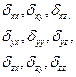
Осы тоғ ыз шаманың жиынтығ ы серпімді кернеудің тензоры деп аталады. Бұ л шамалар ортаның бір нү ктеден екінші нү ктесіне ө ткенде ө згереді, яғ ни координаттар функциясы болып табылады. Егер массалық кү ш ә сер етпейтін болса ғ ана кернеу ортаның барлық нү ктелерінде бірдей болады.

4. Серпімді кернеудің тензоры симметриялық тензор болып табылады, яғ ни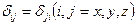

Мұ ны дә лелдеу ү шін заттан қ абарғ алары элементар параллелепипедті бө ліп алайық. Параллелепипеке ә сер ететін ө сіне қ атысты кү ш моменті мынағ ан тең:

3-ші сурет бойынша z осіне байланысты параллелепипедтің айналу моменті тензорлардың жанама элементтеріне тікелей байланысты.

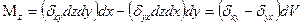
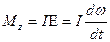
тең діктің оң жағ ындағ ы шама тең діктің сол жағ ындағ ы шамадан тез нольге айналады.Осы тең діктен біз 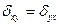керну тензорының симметрия болатынына кө зіміз жетеді.

Мұ ндағ ы жә не ө сіне қ атысты инерция моменті жә не бұ рыштық жылдамдық. Бірақ инерция моменті масса мен параллелепипедтің сызық тық ө лшемдерінің квадратына кө бейтіндісіне пропорционал болады, яғ ни параллелепипед кө лемімен салыстырғ анда жоғ ары дә режедегі шексіз кіші шама болады. Егер параллелепипедті нү ктеге дейін кішірейтсек, онда тең діктің оң бө лігі сол бө лігіне қ арағ анда ертерек нольге айналады. Нә тижесінде аламыз. Сә йкесінше жә не болады.

5.X, Y, Z координаттар системасын серпімді кернеудің тензорының барлық диагональ емес элементтері нольге тең болатындай етіп таң дап алуғ а болады, яғ ни егер мұ ны дә лелдеу қ ажат емес, себебі серпімді кернеудің тензоры симметриялы болады. Осылайша осы нү ктедегі серпімді кернеу ү ш шамамен сипатталады. Оларды деп белгілеуге де болады. Оларғ а сә йкес келетін координата осьтері тензордың бас осьтері деп аталады.