Лекция 6. Уравнения Лагранжа II рода.

Найдем слагаемое с номером i в правой части (5.7), используя выражения (5.3).

.

Здесь использованы два тождества Лагранжа

, .

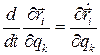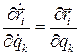После суммирования получим обобщенную силу инерции

.

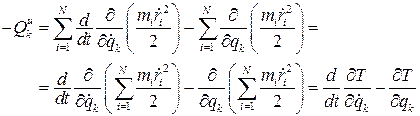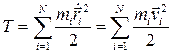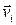Здесь величина , где -скорость i -ой точки, есть, очевидно, кинетическая энергия механической системы.

Окончательно получим

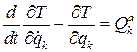, k=1, 2,..., s, (6.1)

где s — число степеней свободы, — кинетическая энергия, 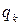, , 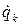- обобщенная координата, обобщенная скорость и обобщенная активная сила с порядковым номером 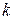данной механической системы.

Составление уравнений движения в форме (6.1) сводится к выполнению ряда формальных действий

· выбрать обобщенные координаты — параметры любой геометрической или физической природы, однозначно определяющие положение системы в любой момент времени;

· записать выражение кинетической энергии системы в виде суммы кинетических энергий точек и тел системы через инерционные параметры (массы точек и тел, моменты инерции тел) и обобщенные координаты и скорости;

· получить выражения производных кинетической энергии, входящие в левую часть (6.1);

· записать выражение виртуальных работ сил системы при варьировании каждой обобщенной координаты, коэффициенты перед вариацией соответствующей обобщенной координаты дают формулу для обобщенной силы, соответствующей этой обобщенной координате.

Для применения полученных уравнений Лагранжа II рода на практике необходимо получить рабочие формулы вычисления виртуальных работ и кинетической энергии системы, что в свою очередь, требует разобраться с инерционными характеристиками механических систем и тел.

Вычисление обобщенных сил. Существует три способа вычисления обобщенных сил.

Первый способ предполагает прямое вычисление коэффициентов при вариациях обобщенных координат в выражении виртуальной работы. Удобнее здесь варьировать не все сразу обобщенные координаты, а по одной. Записывается выражение работы на виртуальном перемещении системы, отвечающем вариации только одной обобщенной координаты, например, с номером k — 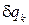, как алгебраическую сумму виртуальных работ активных сил, приложенных к телам и точкам механической системы . Затем, вынося за скобки общий сомножитель — вариацию обобщенной координаты 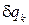, получим выражение для обобщенной силы

.

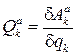Для системы с несколькими степенями свободы такую операцию следует проделать столько раз, сколько обобщенных координат.

Второй способ основан на зависимостях типа (5.3), заданных в явном виде. Тогда обобщенные силы определятся выражением (5.6)

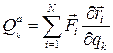, k=1, 2, …, s.

Третий способ опирается на знание потенциальной энергии системы как функции координат ее точек . Подставляя в нее выражения (5.3), получим зависимость потенциальной энергии от обобщенных координат 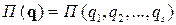, а виртуальная работа будет

.

Сравнивая коэффициенты при одинаковых вариациях, найдем

.

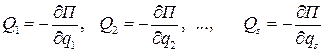Понятно, что лучше сразу по возможности построить функцию потенциальной энергии системы от обобщенных координат .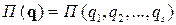

Пример составления уравнений Лагранжа II рода. Найти ускорение бруса, перемещающегося по каткам на наклонной плоскости, составляющей угол a= 30⁰ с горизонтальной плоскостью (рис. 6.1). Масса бруса 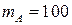кг, массы цилиндрических катков одинаковы и составляют кг. Коэффициент трения качения каждого катка составляет 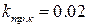м, а радиус 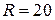см.

Решение. Механическая система, состоящая из бруса и двух катков, имеет одну степень свободы. Выберем в качестве обобщенной координаты перемещение бруса вдоль наклонной плоскости . Тогда ее вариацию (виртуальное перемещение бруса вдоль наклонной плоскости вниз) обозначим .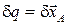

Найдем кинетическую энергию системы, учитывая, что кинетические энергии катков одинаковы.

.

Здесь — кинетическая энергия поступательно движущегося бруса:

.

Рис. 6.1

— кинетическая энергия катков, которую найдем по формуле для плоскопараллельного движения твердого тела

,

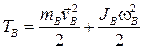где 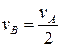— скорость центров масс катков, 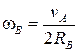— угловая скорость качения катков, — момент инерции катка относительно собственного центра, где — радиус катка.

Окончательно кинетическая энергия системы будет

.

Получим выражения соответствующих производных в (6.1).

так как в выражение кинетической энергии системы координата 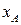явно не входит.

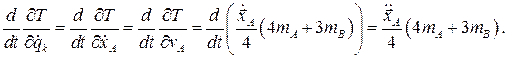(6.2)

Составим выражение виртуальных работ активных сил системы. Здесь это будут только силы тяжести бруса и катков.

,

,

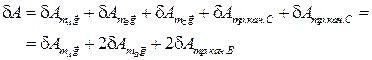
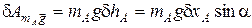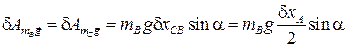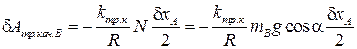
где 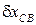— перемещение вдоль наклонной плоскости центров тяжести катков.

Таким образом, виртуальная работа сил системы будет иметь вид

.

Откуда найдем обобщенную силу, как коэффициент перед вариацией обобщенной координаты

. (6.3)

Подставим (8.2) и (8.3) в уравнения (5.1), получим

,

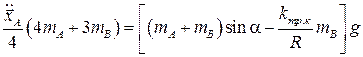или

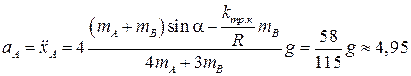м/с ². (6.4)

Таким образом брус будет двигаться вниз равноускоренно с ускорением 4, 95 м/с².

Замечания. Обычно вызывает определенную трудность трактовка знака результата, который получается при изменении направления виртуального перемещения 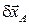, показанного на рис. 6.1 пунктирной стрелкой. Часто заранее неизвестно направление движения системы. В этом случае варьировать можно «наугад», так как виртуальное перемещение не обязано привязываться к действительному движению, поэтому мы вправе направить его куда угодно. Допустим, что в предыдущей задаче мы дадим виртуальное перемещение по пунктирной стрелке. В этом случае левая часть уравнений (6.2) не меняется, а при вычислении правой части, в (6.3) появится знак «-» в работах сил тяжести и знак «+» в работе трения качения. В итоге знак «-» перейдет и в формулу результата ‑ ускорения бруса (6.4). Это, конечно, не будет свидетельствовать о том, что брус двигается замедленно. На самом деле, при вычислении обобщенной силы через виртуальную работу, мы фактически записываем проекции сил системы на направление виртуального перемещения. Поэтому и результат, даваемый формулой (6.4), надо трактовать, как проекцию вектора обобщенного ускорения бруса 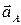на это направление. Таким образом, сделаем вывод, что брус будет двигаться вниз с постоянным ускорением 4, 95 м/с ².

При наличии сил трения их надо направлять в соответствии с направлением действительного движения. Варьирование координат не всегда можно связать с действительным движением. В этом случае, могут появиться выражения для виртуальных работ сил трения со знаком «+», как в рассмотренном примере при виртуальном перемещении бруса по пунктирной стрелке. С формальной точки зрения это не должно смущать, так как это виртуальные, а не действительные работы. Другое дело, что, часто, не решив до конца задачу, мы не знаем направления действительных перемещений точек, а, значит, направлений сил трения. В этом случае может понадобиться решить несколько задач, делая различные предположения о направлении этих сил. И остановиться надо на логически оправданном решении. Иногда удается учесть аналитически знаки проекций сил трения, связав их с алгебраическими значениями скоростей соответствующих тел и точек.