Интегрируя дифференциальное уравнение, получают

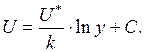
Следовательно, в потоке, находящемся в условиях турбулентного режима, скорости у стенки изменяются по логарифмическому закону.

Зависимость получена для области потока, движущегося около стенки трубы. Естественно, что возникло стремление распространить эту зависимость на весь поток в целом.

На основании опытов Никурадзе обычно считают, что коэффициент 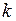для труб имеет постоянное значение и равен 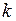=0, 4 для всего живого сечения трубы.

Опыты Шевелёва показали, что этот коэффициент не является постоянным и, в частности зависит от диаметра трубы. Вместе с тем для получения приближённых решений можно принять 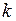=const =0, 4.

Поэтому постоянную интегрирования С получают из условий, что при 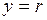скорость в трубе достигает наибольшего значения и равна U_{max .}

Следовательно,

или

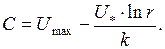
Тогда зависимость для определения U будет

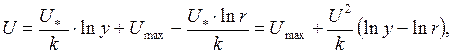
или

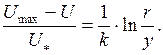
Приняв 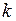=0, 4 и переходя к десятичным логарифмам, получим

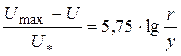
или окончательно

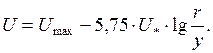
Пользуясь формулами, можно, определить местные скорости в различных точках живого сечения трубы и построить эпюру скорости.

Идеальная или невязкая жидкость является упрощенной моделью реальной (вязкой) жидкости. По предположению, идеальная жидкость имеет все свойства реальной, кроме вязкости, поэтому для получения уравнения ее движения можно применить уравнения Навье ‑ Стокса, положив 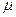= 0. Тогда уравнения движения вязкого газа и движения вязкой несжимаемой жидкости упрощаются и принимают вид

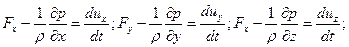
Выражение называют уравнениями Эйлера. Они описывают движение сжимаемой и несжимаемой идеальной жидкости. Их векторные формы легко получить из соответствующих уравнений Навье ‑ Стокса, положив в них v =0.

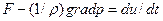
т. е.

,

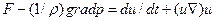и

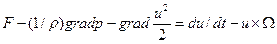
Удобную для интегрирования форму уравнения для сжимаемой жидкости можно получить, предположив баротропность процесса и введя функцию давления. Тогда:

Для несжимаемой жидкости

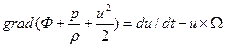
Используя обозначение, 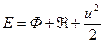запишем уравнение в компактной векторной форме

или в проекциях на оси координат

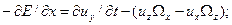
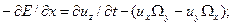
Уравнения Эйлера для несжимаемой жидкости вместе с уравнением неразрывности образуют замкнутую систему. Для сжимаемого газа эту систему необходимо дополнить по меньшей мере еще одним уравнением, например, выражающим условие баротропности или другое термодинамическое соотношение.

Граничные условия на твердых поверхностях для идеальной и вязкой жидкостей существенно различны. При движении идеальной жидкости отсутствует прилипание частиц к твердым поверхностям и жидкость скользит вдоль стенки. Граничным условием в этом случае служит непроницаемость границы, что для неподвижной стенки означает равенство нулю на ней нормальной составляющей скорости жидкости 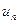│ с=0.

Это условие означает, что вектор скорости касателен к граничной поверхности, т. е. последняя является линией тока. Поэтому любую линию тока в идеальной жидкости можно принять за твердую границу, не нарушив структуры течения.

Если движение идеальной жидкости потенциальное, то условию можно придать вид

,

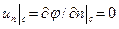где — потенциал скорости.

В случае плоского течения, для которого существует функция тока 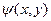, граничное условие на твердой поверхности можно записать в виде

,

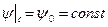откуда следует, что твердая стенка является одной из линий тока, значение функции тока на которой равно .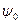

Если граничная поверхность задана уравнением 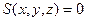, то 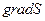есть вектор, нормальный к этой поверхности. Значит, условие равносильно условию ортогональности вектора скорости на стенке u|с и вектора 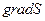. Следовательно, скалярное произведение этих векторов на стенке равно нулю:

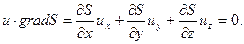
Для подвижной твердой границы используется условие безотрывности течения и непроницаемости стенки, которое сводится к равенству нормальных составляющих скоростей 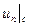с жидкости и 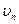стенки:

=

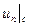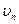
Если подвижная граничная поверхность задана уравнением 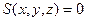, то последнему условию можно придать иную форму. При безотрывном движении частицы ее координаты 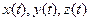должны в любой момент удовлетворять уравнению граничной поверхности, т. е. 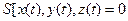. Так как ,

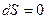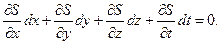
и, учитывая, что 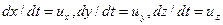‑ и, получим граничное условие на подвижной стенке

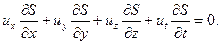
Граничное условие на свободной поверхности для идеальной жидкости, как и для вязкой, имеет вид

.
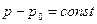