Уравнение Навье-Стокса. Граничные и начальные условия

Уравнения движения вязкой жидкости. Уравнение неразрывности. Развернутая форма уравнений Навье-Стокса для несжимаемой жидкости. Граничные и начальные условия.

Подставив в уравнения движения (9.3) выражения (10.6), получим

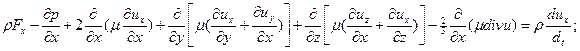
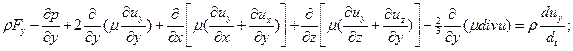
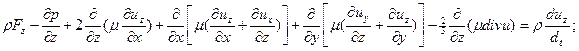
Эти уравнения называются уравнениями Навье ‑ Стокса; их используют для описания движений вязких сжимаемых жидкостей и газов.

Уравнения движения невязких жидкостей и газов легко получить из уравнений Навье ‑ Стокса как частный случай при 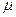= 0; для несжимаемых жидкостей следует принять ρ = const.

Система уравнений Навье ‑ Стокса незамкнута, так как содержит шесть неизвестных: 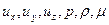. Еще одним уравнением, связывающим эти неизвестные, является уравнение неразрывности

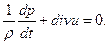
В качестве уравнений, замыкающих систему, используют уравнения состояния среды и зависимости вязкости от параметров состояния. Во многих случаях приходится применять также другие термодинамические соотношения.

Для несжимаемой жидкости (ρ = const) в большинстве случаев вязкость можно считать постоянной, что позволяет значительно упростить уравнения (11.1). После простых преобразований, учитывая, что 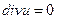, получаем

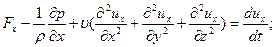
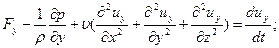(11.2)

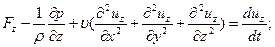
Если раскрыть полные ускорения 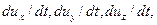выделив в них локальную и конвективную части, то получим развернутую форму уравнений Навье ‑ Стокса для несжимаемой жидкости:

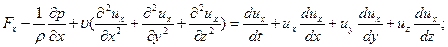
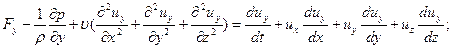
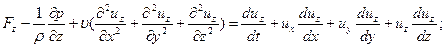
Вместе с уравнением неразрывности 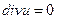уравнения (11.2) образуют замкнутую систему для определения функций .

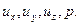Представим уравнения Навье ‑ Стокса в векторной форме. Для этого умножим первое из них на i, второе — на j, третье — на k и сложим. Получим

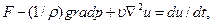(11.3)

где .

Формулы (11.2) или (11.3) могут быть истолкованы как уравнения второго закона Ньютона в форме, специфической для вязкой несжимаемой жидкости. Действительно, их правые части представляют собой отнесенные к единице массы произведения массы на ускорения, а левые сумму отнесенных к единице массы сил, в числе которых массовая сила 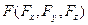, силы давления 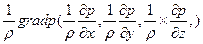и вязкости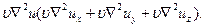

Выделяя уравнение (11.3) представим в виде

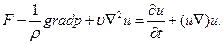(11.4)

Для получения одной употребительной формы уравнения (11.3) используем формулу векторного анализа

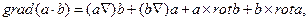
где 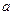и 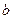— произвольные вектора.

Правильность этой формулы можно проверить непосредственным вычислением.

Пусть 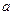= = 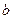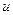. Тогда

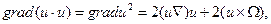
где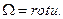

Разрешая это уравнение относительно конвективного ускорения Громеки - Ламба движения вязкой жидкости

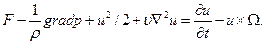(11.4)

Считая что массовые силы обладают потенциалом, т е 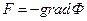и учитывая, что при 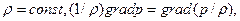уравнение (11.4) приведем к виду

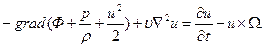(11.5)

Уравнения Навье ‑ Стокса в форме (11.5) удобны для решения ряда задач динамики вязкой жидкости.

Во многих задачах течение вязкой жидкости можно описывать, пользуясь цилиндрической системой координат. Уравнения Навье - Стокса в этой системе имеют вид

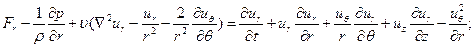
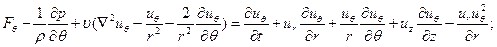(11.6)

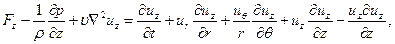
Где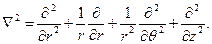

Вместе с уравнением неразрывности уравнения (11.6) образуют замкнутую систему уравнений движения несжимаемой жидкости в цилиндрических координатах.

Общая задача гидромеханики состоит в определении функций 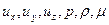с помощью системы уравнении Навье ‑ Стокса (11.1) или (11.2), уравнения неразрывности и дополнительных соотношений, замыкающих систему. Таким образом, гидродинамическая задача сводится к математической задаче получения решений системы нелинейных дифференциальных уравнений в частных производных второго порядка. Математическая теория таких систем разработана пока недостаточно и для них нет общей формулировки и доказательства теорем существования и единственности. Однако для частных видов системы (11.2), описывающих определенные классы течений, такие теоремы сформулированы и доказаны.

Поскольку общие решения дифференциальных уравнений в частных производных содержат произвольные функции, для получения конкретных решений нужно их определить. Для этого должны быть заданы начальные и граничные условия, которым удовлетворяют найденные решения.

Под начальными условиями понимают заданные значения искомых функций в начальный момент времени во всей области течения, а под граничными ‑ заданные значения, которые должны принимать искомые функции в точках граничных поверхностей во все моменты времени.

Рассмотрим начальные и граничные условия для неустановившегося движения несжимаемой жидкости . В качестве начальных условий задается распределение скоростей 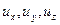в области течения в начальный момент времени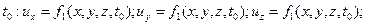

Задавать давление нет необходимости, так как для момента t₀ его можно определить из исходных уравнений по известным 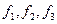. Граничные условия зависят от характера границ. На неподвижной непроницаемой стенке они заключаются в равенстве нулю на ней скоростей жидкости (u =0), так как частицы вязкой жидкости прилипают к стенке. Это условие имеет вид

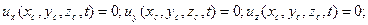
где 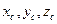— координаты точек твердой стенки.

На подвижной непроницаемой границе скорость жидкости совпадает со скоростью движения самой границы. Границей области течения может служить свободная поверхность. Ее форма, а также значения скоростей на ней неизвестны и сформулированные выше кинематические условия для такой границы нельзя задать. Однако на свободной поверхности давление во всех точках постоянно и равно внешнему давлению 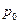. Это обстоятельство; может быть истолковано как одно из граничных условий

.

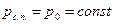Точные решения общей задачи гидромеханики удается получить только для простейших граничных условий. Поэтому большое значение приобретает получение из уравнений движения некоторых частных соотношение, устанавливающих связи между параметрами движения, справедливые при некоторых ограничениях или для отдельных классов течений. Таким соотношением является уравнение Бернулли.