Взаимное пересечение поверхностей

⇐ ПредыдущаяСтр 12 из 13Следующая ⇒

11.1.Пересечение криволинейной и гранной поверхностей

Линией пересечения (ЛП) криволинейной и гранной поверхностей является пространственная замкнутая ломаная, вершинами которой являются точки пересечения ребер многогранника с криволинейной поверхностью, а звенья - линии пересечения криволинейной поверхности с гранями многогранника. В случае врезки ЛП состоит из одной ломаной, в случае проницания - из двух (рис.80).

Особые точки ЛП:

· вершины ломаной – точки пересечения ребер многогранника с поверхностью вращения;

· опорные точки (граничные точки видимости) - точки пересечения очерковых образующих криволинейной поверхности с гранной поверхностью;

· особые точки кривых - звеньев ЛП: центры, вершины, точки на концах осей и т.д.

Построение ЛП сводится к двум выше уже рассмотренным выше задачам: а) построить точки пересечения прямой с поверхностью и б) построить сечение поверхности плоскостью.

Задача. Построить проекции конуса с призматическим вырезом (рис.81).

Алгоритм решения

1. Определяем тип линии пересечения (ЛП). Т.к. ни одна из поверхностей не пересекает другую полностью, то данный случай - врезка и ЛП состоит из одной ломаной.

Звенья ЛП – конические сечения: грань призмы Г (Г₂), перпендикулярная оси конуса,

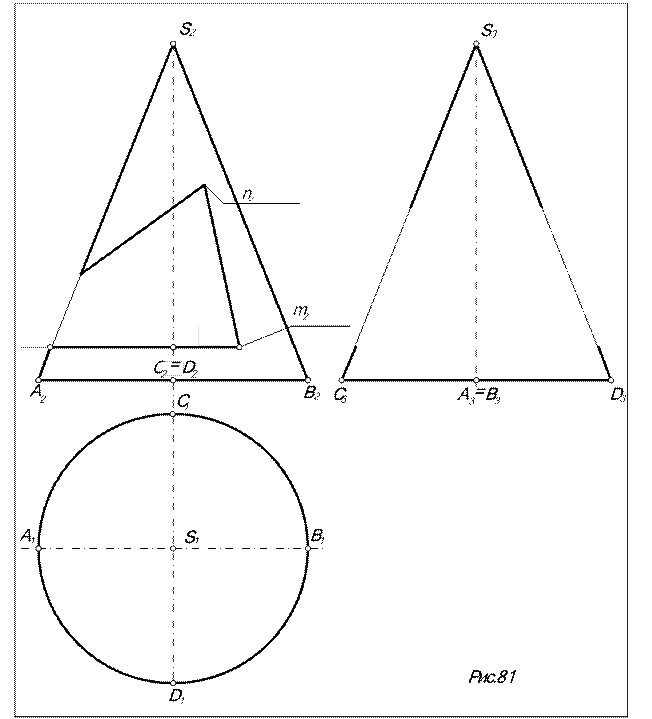пересекает конус по дуге окружности; грань призмы L (L₂), плоскость которой проходит через вершину конуса, - по образующим конуса; грань призмы S (S₂), наклоненная к оси конуса (b> a), - по дуге эллипса.

Т.к. грани призмы фронтально проецирующие, то на П₂ проекция ЛП совпадает с проекцией призматического выреза.

2. Находим особые точки ЛП сначала на известной фронтальной проекции:

-вершины ломаной – точки пересечения ребер n и m c поверхностью конуса - совпадают с проекциями самих ребер, т.к. ребра – фронтально проецирующие: n₂ = 1₂ =2₂, m₂= 3₂=4₂.

-центр О (О₂) и точки на концах осей эллипса. Продлив грань S (S₂) до пересечения с очерковой образующей S₂ B₂ находим фронтальную проекцию большой оси эллипса 5₂6₂, разделив которую пополам находим центр О (О₂) и точки 7₂= 8₂ на концах малой оси.

- граничные точки видимости находим как результат пересечения вырожденных про-екций граней призматического отверстия с очерковыми образующими конуса: граничные точки видимости на П₂ – 5₂= S₂А₂ S₂, 13₂ = S₂А₂ Г₂, граничные точки видимости на

П₃– 9₂= S₂C₂ S₂, 10₂= S₂D₂ S₂, 11₂= S₂C₂ Г₂, 12₂ = S₂D₂ Г₂.

На остальных проекциях найденные на П₂ точки находим либо по их принадлежности образующим, на которых они расположены, либо по их принадлежности конусу. Например, точки 7 и 8 находим, проведя параллель радиуса r. При этом для достижения требуемой точности построений не рекомендуется пользоваться постоянной чертежа к₀ и ломаными линиями связи между П₁ и П₃ (см. задачу на рис.77).

3. Случайные точки (на дуге эллипса) выбираем произвольно на П₂, а другие их проекции находим по принадлежности поверхности конуса, как точки 7, 8.

4. Построенные точки соединяем с учетом их видимости на проекциях, определяя види-мость по представлению. При взгляде сверху ЛП видима полностью, не видны только ребра m и n отверстия. На П₂ видимые и невидимые части ЛП совпадают. При взгляде слева (на П₃) видимы части ЛП, лежащие на левой половине конуса, а также участки прямых (13) и (24) из-за отсутствия материала, их закрывающего.

Задача. Построить проекции сферы с призматическим вырезом (рис.82).

Алгоритм решения

1. Определяем тип линии пересечения (ЛП). Т.к. поверхность сферы пересекает поверх-ность призматического отверстия полностью, то данный случай - проницание (а точнее – граничный случай, т.к. одно из ребер призмы не пересекает, а касается сферы) и ЛП состоит из одной ломаной, звеньями которой являются дуги окружностей.

Грани Г (Г₂) и D (D₂) параллельны П₁ и расположенные в них сечения сферы проециру-ются в П₁ в натуральную величину в виде дуг окружностей, а в П₃ — в виде горизонтальных отрезков. Грань S (S₂) наклонена к П₁ и П₃ и дуга окружности, в ней расположенная, проеци-руется в эти плоскости проекций в виде дуг эллипса. Грань L (L₂) параллельна П₃ и располо-женное в ней сечение сферы проецируется в П₃ в натуральную величину в виде дуг окружно-стей, а ви П₂ — в виде отрезков.

2. Т.к. грани призмы фронтально проецирующие, то на П₂ нам известна проекция ЛП: она совпадает с проекцией призматического выреза и мы можем отметить все особые точки ЛП: вершины 1, 2, 3, 4, граничные точки видимости на П₁ (5, 6) и на П₃(4, 7), а также центр окружности О, расположенной в грани S (S₂), и её горизонтальный диаметр 8-8 ^/. Проекции центра О₂ и точек 8₂ и 8₂ ^/ можно найти либо делением пополам диаметра 1-1^*=1₁-1₁^*, либо как результат пересечения вырожденной проекции грани S₂ с опущенным на неё из центра сферы О₂^* перпендикуляром.

Т.к. три из четырёх граней призматического отверстия пересекают сферу по геометри-чески простым линиям (окружностям), которые в свою очередь проецируются в виде геомет-рически простых линий, то оптимальным алгоритмом решения является построение сразу проекций этих линий на П₁ и П₃ с попутным нахождением проекций особых точек ЛП.

Для построения горизонтальной проекции дуги окружности в грани Г(Г₂) необходимо найти её центр и радиус. Центр дуги находим как результат пересечения вырожденной про-екции грани Г₂ с вертикальной осью сферы, а её радиус R_Г равен расстоянию от центра до 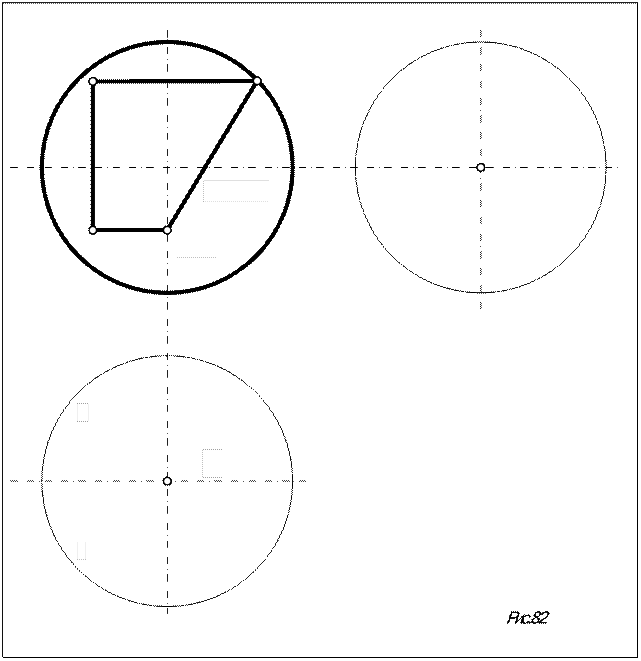очерка сферы. Построив на П₁ окружность радиусом R_Г находим по принадлежности ей осо-бые точки ЛП: 1₁ - проекцию точки, общей для двух ветвей ЛП; 2₁ и 2₁ ^/ - вершины ЛП и точки 7₁ и 7₁ ^/ - граничные точки видимости на П₃. Дугу 2₁-1₁-2₁ ^/ проводим сплошной основной линией, т.к. она расположена на верхней полусфере и видима на П₁.

Для построения профильной проекции дуги окружности в грани Г находим точки 1₃, 7₃ и 7 ₃ ^/ как результат пересечения её вырожденной проекции Г₃ спроекциями главного меридиана т₃ и профильного очерка р₃ сферы соответственно. Точки 2_з и 2_з' находим, откладывая на Г₃ от вырожденной проекции плоскости симметрии Ф₃ отрезки, равные расстоянию между горизонтальной вырожденнойпроекцией Ф₁ и проекциями точек 2₁ и 2₁^/. Т.к. дуги 2-7 лежат на левой полусфере, то на П₃ они видимы, и поэтому соединяем их сплошной основной линией, а дуга 7₃ - 1₃ -7₃^/ невидима на П₃, т.к. лежит на правой полусфере.

По аналогичному алгоритму строим горизонтальные и профильные проекции дуг окружностей, расположенных в гранях D и L.

3. Для построения горизонтальной и профильной проекций дуги окружности в грани S, которая проецируется на П₁ и П₃ в виде дуг эллипса, необходимо найти принадлежащие им проекции особых точек. Проекции центра эллипса О₁ и О₃ находим, используя уже найденную его проекцию О₂, по принадлежности вырожденным проекциям плоскости симметрии Ф (Ф₁, Ф₃,). Проекции точек 8 и 8 ^/ на П₁ и П₃ находим из условия равенства диаметров окружности 1-1^* = 1₂-1₂^* = 8 - 8 ^/= 8₁ - 8₁^/ = 8₃ - 8₃^/. Проекции точек 1, 4 и 4', 6 и 6' находим по принадлежности соответствующим очеркам сферы. Сначала находим профильные проекции точек 4₃, 4₃^/ по принадлежности меридиану p₃, а затем – их горизонтальные проекции 4₁, 4₁^/, отложив на p₁ от Ф₁ отрезки, равные расстоянию между проекциями 4₃, 4₃^/ и Ф₃. Проекции точек 6 и 6' находим аналогичным образом сначала на П₁, а затем на Ф₃.

Случайные точки эллипса на П₁ и П₃ можно построить либо методом секущих плоскостей (как точки 1, 2, 7), либо используя свойство симметрии эллипса. Например, строим точку 4₁ ^*, симметричную относительно оси эллипса 8₁- 8₁ ^/ранее найденной точке 4.

4. Построенные точки эллипса соединяем плавной кривой с учетом их видимости на проекциях, определяя видимость по представлению. Участок эллипса 1-6 лежит на верхней полусфере и виден на П₁. Остальная часть эллипса, лежащая на нижней полусфере, также ви-дима сверху, т.к. не закрывается остатком верхней полусферы, ограниченным окружностью R_Г. Аналогично строим профильную проекцию эллипса и определяем его видимость. При этом часть проекции эллипса, заслоняемую остатком левой полусферы, ограниченным окружностью радиуса R_L.

5. Достраиваем горизонтальную и профильную проекции сферы с отверстием с учетом видимости очерков поверхностей. Часть горизонтального очерка - экватора п - между точка-ми 5 и 6 вырезана отверстием (см. проекцию на П₂), а остальная часть экватора видима и обводится сплошной основной линией. По аналогичной причине отсутствует часть профиль-ного очерка сферы между точками 4 и 7. Ребра призматического отверстия проходят внутри сферы и на П₁ и П₃ невидимы.

11.2.Пересечение поверхностей вращения второго порядка

Линия пересечения поверхностей вращения 2-го порядка в общем случае – про-странственная замкнутая кривая 4-го порядка, состоящая из двух линий в случае прони-цания или из одной - в случае врезки.

Особые точки ЛП - точки пересечения очерковых образующих одной поверхности с другой поверхностью и точки пересечения очерковых линий второй поверхности с первой поверхностью.

Точки ЛП в общем случае находятся способом вспомогательных секущих поверх-ностей-посредников, в роли которых могут выступать плоскости и сферы.

11.2.1.Способ секущих плоскостей (рис.83)

1.Проводится вспомогательная плоскость S, пересекающая обе поверхности по гео-метрически простым линиям, которые проецируются также в виде геометрически простых линий (прямых или окружностей).

2. Строятся линии m и n пересечения поверх-ностей D и Ф плоскостью S: m = Ф S, n =D S.

3. Находятся точки 1 и 2 пересечения построен-ных линий пересечения m и n: 1, 2 = m n.

Это и есть искомые точки ЛП заданных поверхностей D и Ф. Проведя достаточное число секущих плоскостей, находим достаточное количество точек ЛП.

Задача. Построить линию пересечения сферы и конуса (рис.84).

Алгоритм решения

1. Определяем тип линии пересечения. Пересекаются поверхности вращения 2-го порядка, случай врезки: ЛП - одна замкнутая пространственная кривая 4-го порядка. Обе поверхности имеют общую фронтальную плоскость симметрии. Следовательно, фронтальные проекции видимой и невидимой на П₂ ветвей ЛП - совпадают и замкнутая кривая на П₂ проецируется в виде разомкнутой.

2.Построение особых точек ЛП.

Главные меридианы сферы m и ASB конуса лежат в одной плоскости (фронтальной плоскости симметрии) и, следовательно, пересекаются. Поэтому граничные точки видимости на П₂ находятся как результат пересечения проекций главных меридианов сферы и конуса:

1₂, 2₂= m₂ A₂S₂..

На П₁ эти точки находятся по принадлежности меридианам.

Точки пересечения горизонтального очерка сферы (экватора n) с конусом находим методом вспомогательных секущих плоскостей:

· проводим плоскость Г(Г₂) через экватор сферы,

· строим линии пересечения сферы и конуса: cфера пересекается по экватору n, который уже построен на обеих проекциях, а конус – по окружности радиуса R_Г,

· находим проекции точек 3₁ и 4₁ пересечения этих окружностей на П₁, а затем фронтальные проекции этих точек по принадлежности Г₂.

3. Случайные точки ЛП находим тем же способом, что и точки 3 и 4, проводя горизонтальные секущие плоскости S и D. При этом для упрощения построений проводим их на

4. Видимость ЛП и очерков поверхностей определяем по представлению.

11.2.2.Способ концентрических секущих сфер

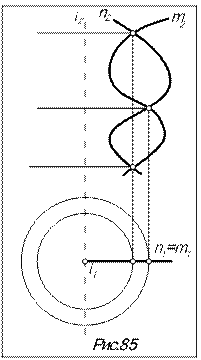
В основе способа - теорема: две соосные поверхности вращения (рис.85) пересекаются по окружностям, число которых равно числу точек пересечения главных полумеридианов m и n поверхностей. Эти окружности являются общими для обеих соосных поверхностей параллелями, плоскости которых перпендикулярны общей оси вращения.

Это обстоятельство позволяет использовать в качестве вспомогательных секущих элементов не плоскости, а сферические поверхности.

Способ секущих сфер применяется в случае,

- если решение задачи методом секущих плоскостей либо невозможно, либо графически усложнено,

- если оси заданных поверхностей пересекаются: можно провести сферу, соосную обеим поверхностям,

- если оси заданных поверхностей образуют общую плоскость симметрии, параллельную какой-либо плоскости проекций: окружности - линии пересечения сферы с поверхностями - проецируются в виде простых линий окружностей и отрезков прямых.

Алгоритм построения ЛП поверхностей способом концентрических секущих сфер аналогичен алгоритму метода секущих плоскостей:

1. Проводится сфера, соосная обеим заданным поверхностям и пересекающая их.

2. Строятся окружности - линии пересечения секущей сферы с обеими заданными поверхностями.

3. Находятся точки пересечения построенных окружностей. Это и будут искомые точки ЛП поверхностей.

Выбор параметров секущих сфер:

1.Чтобы сфера была соосна обеим заданным поверхностям, ее центр должен располагаться в точке пересечения осей вращения поверхности.

2. Радиус сферы должен удовлетворять условию Rmаx ³ R ³ Rmin.

Минимальный радиус Rmin секущей сферы определяется из условия, что сфера должна пересекать обе заданные поверхности. Сфера Rmin касается одной из поверхностей и пересекает другую, поэтому Rmin равен большей из нормалей, проведенных из центра сфер к очерковым образующим заданных поверхностей.

Максимальный радиус секущей сферы Rmax определяется из условия, что линии пересечения сферы с заданными поверхностями должны пересекаться между собой, поэтому Rmax равен расстоянию между центром сфер и наиболее удаленной от него точкой пересечения очерковых образующих заданных поверхностей.

Задача: Построить ЛП поверхностей методом концентрических секущих сфер(рис.86).

Алгоритм решения

1. Находим на П₂ точки пересечения очерковых образующих конуса SA и SB и цилиндра e и g. Судя по их горизонтальным проекциям (лежат на одной прямой, параллельной оси проекций x₁₂), эти образующие располагаются в одной фронтальной плоскости и пересекаются: 1₂= S₂A₂ e₂, 2₂ = S₂A₂ g₂, 3₂ = S₂B₂ e₂, 4₂ = S₂B₂ g₂. Горизонтальные проекции этих точек находим по принадлежности соответствующим образующим.

2. Выбираем на фронтальной проекции параметры секущих сфер. Проекцию центра O₂ берем на пересечении осей вращения конуса i₂ и цилиндра j₂ и проводим из O₂ нормали m и n к фронтальным очерковым конуса S₂A₂ и цилиндра е₂.Rmin равен большей из этих

нормалей: Rmin = m. Из этого, кстати, можно сделать вывод, что в месте пересечения поверхностей диаметр цилиндра меньше диаметра конуса и цилиндр полностью пересекается конусом. Значит, мы имеем дело со случаем проницания и ЛП, состоящей из двух замкнутых контуров, располагающихся на поверхности цилиндра. Rmаx принимаем равным расстоянию между центром О₂ и наиболее удаленной от него точкой 2₂ пересечения очерковых образующих поверхностей.

3. Находим на П₂ точки ЛП методом секущих сфер.

3.1. Проводим на П₂ сферу R = Rmin.

3.2. Находим точки пересечения её проекции с проекциями очерковых e₂ и g₂ цилиндра. Соединив полученные точки попарно отрезками, перпендикулярными оси j₂ цилиндра, получим проекции а₂ и а₂^* окружностей, по которым сфера пересекает цилиндр. Находим точки касания проекции сферы Rmin очерковых A₂S₂ и B₂S₂ конуса и, соединив их отрезком, перпендикулярным оси конуса, получим проекцию окружности касания сферы и конуса b₂. Окружности а₂, а₂^* и b₂ лежат на поверхности сферы Rmin и, следовательно, пересекаются (или параллельны как а₂ и а₂^*).

3.3. Находим проекции точек принадлежащих искомой ЛП - точек пересечения построенных окружностей,: 5₂ = 5₂^* = b₂ а₂^*, 6₂= 6₂^*= b₂ а₂. (Для упрощения чертежа точки 5₂^* и 6₂^* условно не показаны). Горизонтальные проекции найденных на П₂ точек 5 и 6 находим по принадлежности параллели b конуса. Для этого строим на П₁ её проекцию b₁ – окружность с центром О₁ и диаметром, равным длине отрезка b₂. Проведя сферу радиусом Rmаx ³ R ³ Rmin, по аналогичному алгоритму находим точки 7, 8, 9 ЛП.

4. Одноименные проекции построенных точек соединяем плавными кривыми с учетом видимости. На П₂ видимые и невидимые участки ЛП совпадают из-за наличия общей для обеих поверхностей фронтальной плоскости симметрии. Последовательность соединения точек: 1-5-7-2 для левого контура и 3-6-8-4 - для правого.

Чтобы построить горизонтальную проекцию ЛП с учетом видимости необходимо дополнительно найти граничные точки видимости на П₁. Это точки пересечения очерковых k и l цилиндра с поверхностью конуса. Сначала находим эти точки (10₂ = 10₂^* и 11₂ = 11₂^*) на П₂ как результат пересечения k₂ и l₂ с уже построенными фронтальными проекциями ЛП, а затем – 10₁, 10₁^*, 11₁, 11₁^* по принадлежности k₁ и l₁. Видимыми на П₁ будут участки ЛП, лежащие на верхней части цилиндра (1-5-7-11 и 3-9-6-10), невидимыми – лежащие на нижней его части.

5. Определяем видимость очерков поверхностей. На П₂ видимыми будут те части очерка конуса, которые лежат вне очерка цилиндра, и те части очерка цилиндра, которые лежат вне очерка конуса. На П₁ видимыми будут те части очерковых k и l, которые расположены правее точек 10 и левее точек 11.

11.3.Особые случаи пересечения поверхностей вращения второго порядка

В общем случае поверхности вращения 2-го порядка пересекаются по пространственным кривым 4-го порядка. Существуют частные случаи, когда такие поверхности пересекаются по плоским кривым второго порядка.

С одним таким случаем - соосными поверхностями - мы познакомились выше. Другие признаки распадения кривой 4-го порядка на плоские кривые 2-го порядка сформулированы в следующих теоремах.

Теорема о двойном прикосновении: если две пересекающиеся поверхности вращения 2-го порядка имеют две точки касания, то линия их пересечения распадается на две плоские кривые 2-го порядка, плоскости которых проходят через прямую, соединяющую точки касания.

Под точкой касания поверхностей понимается такая их общая точка, через которую можно провести плоскость, касательную к обеим поверхностям.

Теорема Монжа: если две пересекающиеся поверхности 2-го порядка описаны около третьей поверхности 2-го порядка или вписаны в нее, то линия их пересечения распадается на две плоские кривые 2-го порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания поверхностей.

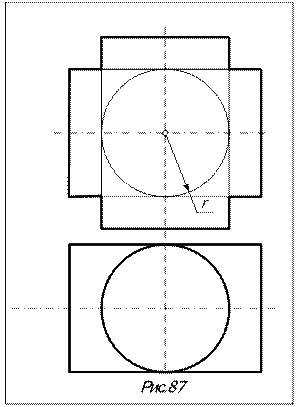На рис.87 показаны два цилиндра вра-щения, описанные вокруг сферы радиуса r. По теореме Монжа они имеют две точки касания А = e l и В = f k, через которые можно провести фронтальные плоскости S (S₁) и S^* (S₁^*), касающиеся обеих цилиндров по образующим e, f и k, l. На П₂ проекции точек А и В, найденные по принадлежности образующим e и f, совпадают (A₂ = B₂), то есть отрезок (АВ) – фронтально проецирующий, и плоскости кривых, по которым пересекаются цилиндры, также фронтально проецирующие и проецируются на П₂ в виде отрезков, проходящих через A₂ = B₂. Для построения этих отрезков достаточно построить еще две пары точек, принадлежащих обоим цилиндрам. Это точки пересечения фронтальных очерковых, лежащих в одной фронтальной плоскости Ф (Ф₁): 1₂= m₂ c₂, 2₂= m₂ d₂, 3₂= n₂ c₂, 4₂ = n₂ d₂.

Cоединив попарно точки 1₂ и 4₂, 2₂ и 3₂ отрезками, получим проекции ЛП цилиндров - двух плоских кривых второго порядка. Т.к. плоскости их наклонены к осям цилиндров, то это эллипсы. На П₁ эллипсы проецируются на окружность – вырожденную проекцию горизонтально проецирующего цилиндра.

⇐ Предыдущая 4 5 6 7 8 9 10 111213 Следующая ⇒

© 2023 :: MyLektsii.ru :: Мои Лекции
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав.
Копирование текстов разрешено только с указанием индексируемой ссылки на источник.