Дисконтирование по простым процентам

Лекция 2

Простые проценты

Наращение простыми процентами (рассматривалось в лекции 1)

Схема простых процентов предполагает неизменность величины, с которой происходит начисление. Пусть исходный инвестируемый капитал равен Р, требуемая доходность – r (в десятичных дробях). Считается, что инвестиция сделана на условиях простого процента, если инвестированный капитал ежегодно увеличивается на величину Р·r. Таким образом, размер инвестированного капитала через n лет будет равен:

F = P + P·r + … + P·r = P + Pnr = P(1+nr), (1)

т.е. проценты начисляются на одну и ту же величину капитала в течение всего срока.

Выражение (1) называется формулой наращения по простым процентам, а множитель (1+nr) – множителем наращения. Очевидно, что множитель наращения равен индексу роста капитала Р за n лет.

Легко видеть, что приращение капитала I = Pnr (2)

пропорционально сроку ссуды и ставке процента, т.е. доход инвестора растет линейно вместе с n.

На практике процентная ставка r может зависеть от величины исходного капитала Р: с увеличением капитала увеличивается и устанавливаемая ставка. Например, если инвестируется капитал до 20 тыс. руб., то устанавливается одна процентная ставка, более 20 тыс. руб. – другая.

Например, найдем величину процента и наращенную сумму за трехлетний кредит в 20 тыс. руб., взятый под 9%. Здесь Р = 20000, n = 3 года, r = 0, 09. I = 20·3·0.09 = 5, 4 тыс. руб., F = P + I = 20 + 5, 4 = 25, 4 тыс. руб.

Дисконтирование по простым процентам

При заключении финансовых соглашений часто приходится решать задачу, обратную задаче нахождения наращенной суммы. Например, по заданной сумме F, которую предполагают получить (или уплатить) через время t, требуется определить величину капитала Р, который необходимо инвестировать в данный момент, чтобы через время t при постоянной процентной ставке r получить сумму F. Аналогичная задача возникает и в случае, когда проценты удерживаются непосредственно при выдаче ссуды.

Как известно из предыдущей лекции, такое движение денежных средств от будущего к настоящему носит название дисконтирования. Говорят, что капитал F дисконтируется; величина удержанных процентов часто называется дисконтом (discount). Иногда так называют учетную ставку. Капитал Р, найденный с помощью процесса дисконтирования суммы F, называется приведенной (современной, текущей, капитализированной) стоимостью. Понятие приведенной стоимости является одним из важнейшим в количественном анализе финансовых операций.

Различают математическое и банковское дисконтирование.

При математическом дисконтировании решается задача нахождения такой величины капитала Р, которая через n лет при наращении по простым процентам по ставке r будет равна F. Решая (1) относительно Р, получим:

(3)

Таким образом, величина Р является приведенной стоимостью величины F. Дисконт-фактор (дисконтный множитель, коэффициент дисконтирования) показывает долю капитала Р в F. Дисконтный множитель представляет собой величину, обратную множителю наращения простых процентов. В качестве ставки дисконтирования используется процентная ставка r. Разность между F и Р называется дисконтом:

(4)

Дисконт не пропорционален ни времени n, ни ставке процента r. При F = 1 и n = 1 из формулы (4) следует, что 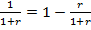. Таким образом, если в качестве денежной единицы рассматривать, например, рубль, то дисконтный множитель представляет собой его разницу между рублем и его процентами за один год.

Пример. Из какого капитала можно получить 3, 4 млн. руб. через 3 года наращением по простым процентам при ставке 12%? Пользуясь формулой (3), где F= 3, 4; n = 3; r = 0, 12, получим: 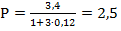млн. руб. D = F – P = 3, 4 – 2, 5 = 0, 9 млн. руб.

В приведенном примере величина дисконта равна величине начисленных процентов, т.е. дисконт определяется через процентную ставку. Однако дисконт, понимаемый как скидка с конечной суммы долга, может быть установлен сразу в виде некоторой суммы (не связанной с процентной ставкой) на все время сделки.

Банковское дисконтирование (или банковский учет) применяется при операции по так называемому учету векселей банком или другим финансовым учреждением.

Согласно международному вексельному законодательству вексель (bill) является письменным безусловным обязательством или указанием векселедателя (заемщика) выплатить в установ­ленный срок определенную сумму предъявителю векселя или лицу, указанному в векселе. Существуют различные виды век­селей: простые, переводные, коммерческие, казначейские и т.д.

Векселя могут оформляться по-разному, однако чаще всего банку приходится иметь дело с суммой к погашению. Рассмот­рим наиболее распространенную ситуацию, когда владелец век­селя на сумму F (сумма к погашению) предлагает банку раньше срока оплаты векселя купить его. Такая покупка векселя у вла­дельца до наступления срока оплаты по цене, меньшей той сум­мы, которая должна быть выплачена по векселю в конце срока, называется дисконтированием векселя. Сама операция дискон­тирования векселя часто называется учетом векселя (bill discounting). Сумма, которую получает векселедержатель при досрочном учете векселя, называется дисконтированной величи­ной векселя.

Таким образом, векселедержателю досрочно выплачивается обозначенная в векселе сумма за вычетом определенных про­центов, удерживаемых банком в свою пользу и нередко назы­ваемых дисконтом. Дисконт (обозначаемый D_d) в этом случае представляет собой проценты, начисленные за время (n) от дня дисконтирования до дня погашения векселя на сумму (F), под­лежащую уплате в конце срока. Если объявленная банком став­ка дисконтирования равна d (учетная ставка), то

D_d=Fnd (5)

и владелец векселя получит

P = F-Fnd = F{1-nd), (6)

где множитель (1 - nd) называется дисконтным множителем или коэффици­ентом дисконтирования.

Очевидно, что чем выше значение дисконтной ставки, тем большую сумму удерживает банк в свою пользу. Учет векселя чаще всего осуществляется способом 365/360.

Пример. Векселедержатель предъявил для учета вексель на сумму 50 тыс. руб. со сроком погашения 28.09.1997 г. Вексель предъ­явлен 13.09.1997 г. Банк согласился учесть вексель по учетной ставке 30% годовых. Определить сумму, которую векселедер­жатель получит от банка.

Величина этой суммы рассчитывается по формуле (6) и при F = 50 тыс. руб., n = 15/360 года, d = 0, 3 составит: P = 50·(1- = 49, 375 тыс. руб. Разность между F (номинальной величиной векселя) и Р (дисконтированной величиной векселя), равная D_d, представля­ет собой комиссионные, удерживаемые банком в свою пользу за предоставленную услугу; в данном примере Dd = 625 руб.

По смыслу правая часть равенства (6) должна быть всегда неотрицательной. Следовательно, должно выполняться неравен­ство 1-nd > 0, что равносильно (так как d > 0) неравенству n . Таким образом, если при достаточно большой учетной ставке d попытаться учесть вексель задолго до срока платежа,

то можно вообще ничего не получить (при n = 1/d), При n > 1/d сумма Р, которую должен получить при учете векселя его вла­делец, становится отрицательной, что лишено смысла. Напри­мер, если d = 0, 5 (учетная ставка в 50%), то должно быть n 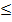2, т.е. учитывать вексель можно не более чем за два года до срока платежа; если d = 2 (ставка в 200%), то должно быть n 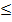0, 5 (учет не более чем за полгода до срока).

Заметим, что при математическом дисконтировании таких ситуаций не возникает: при любой ставке г и любом сроке n всегда Р > 0. Так что учетная ставка более жестко отражает временной фактор, чем ставка г.

Пример. Банк 12.04.97 учел два векселя со сроками погашения соот­ветственно 20.05.97 и 11.06.97. При этом в результате примене­ния учетной ставки 18% годовых банком были удержаны ко­миссионные в размере 885 руб. Найти номинальную стоимость второго векселя, если первый вексель предъявлен на сумму 15 тыс. руб. Используется способ 365/360. 54

Первый вексель учтен за 38 дней до срока погашения, второй — за 60 дней. Обозначая F = 15 тыс. руб., n = 38/360 года, d = 0, 18, по формуле (5) определим комиссионные, удержан­ные банком за согласие учесть первый вексель:

тыс. руб., т.е. руб.

Таким образом, дисконт от учета второго векселя составит:

= 600 руб.

Из формулы (5) следует, что F = 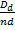. Поэтому, обозначая D_d = 600 руб., n = 60/360 года, d = 0, 18, получим: F = = 20000 руб.

Следовательно, номинальная стоимость второго векселя рав­на 20 тыс. руб.

Возможна ситуация, когда вексель предусматривает начис­ление простых процентов на сумму по обязательству по про­центной ставке. В этом случае при учете векселя исходят из наращенной к сроку погашения векселя суммы.

В принципе при учете денежных обязательств (и, в частно­сти, векселей) банк может использовать процентную ставку и математическое дисконтирование. В этом случае владелец де­нежного обязательства получит сумму, определяемую формулой (3), а комиссионные банка находятся по формуле (4).

Естественно, математическое дисконтирование выгоднее для векселедержателя, а банковское дисконтирование — для банка.