
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятия и операции нечёткой логики.
|
|
Наиболее сложным и ответственным этапом в процессе управления является принятие решений. Моделирование процессов принятия решений требует использования аппарата понятий с нечёткими границами и высказываний с многозначной шкалой истинности.
Построение моделей принятия решений для задач, имеющих нечётное словесное описание, базируется на понятиях нечёткого множества и лингвистической переменной. Эти понятия употребляются в случаях, когда описываемый объект может вполне определённо принадлежать к интересующему нас классу, может и не принадлежать к нему, возможны и промежуточные градации принадлежности, которые можно обозначить числами, находящимися в диапазоне от 1 до 0. После этого появляется возможность перейти от словесных описаний элементов принятия решения к числовым.
Нечётким множеством А (Alternative) на универсальном множестве U (Universum), состоящем из элементов u, называется совокупностью пар
 , (4.34)
, (4.34)
где 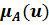 - отображение множества U в единичный отрезок
- отображение множества U в единичный отрезок 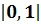 , называемое функцией принадлежности нечёткого множества А.
, называемое функцией принадлежности нечёткого множества А.
Нечёткое множество А состоит из совокупности пар чисел, когда каждому числу из множества U ставится в соответствие число  , причём имеет место неравенство
, причём имеет место неравенство
 . (4.35)
. (4.35)
Значение функции принадлежности 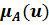 для любого элемента u называется степенью принадлежности. Нечёткое множество является количественной характеристикой нечёткого понятия, а степень принадлежности
для любого элемента u называется степенью принадлежности. Нечёткое множество является количественной характеристикой нечёткого понятия, а степень принадлежности 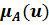 есть субъективная оценка лицом, принимающим решение, того, насколько элемент u соответствует понятию, формализуемому нечётким множеством А. Можно также полагать, что степень принадлежности в какой-то мере соответствует вероятности того, что элемент u будет отнесён к множеству А. Множество значений u, для которых имеет место
есть субъективная оценка лицом, принимающим решение, того, насколько элемент u соответствует понятию, формализуемому нечётким множеством А. Можно также полагать, что степень принадлежности в какой-то мере соответствует вероятности того, что элемент u будет отнесён к множеству А. Множество значений u, для которых имеет место  > 0 согласно соотношению (4.35), называется носителем SA (Set A) нечёткого множества А.
> 0 согласно соотношению (4.35), называется носителем SA (Set A) нечёткого множества А.
При графическом отображении нечёткого множества значение носителя нечёткого множества откладывают по оси абсцисс, а степень принадлежности – по оси ординат, формируя тем самым кривую функцию принадлежности. Пример отображения посредством нечёткого множества нечёткого понятия «скорость движения ν около 130 км/ч» приведён на рис.4.3.
| 0, 5 |
| μ |
| ν, км/ч |
Рис.4.3. Функция принадлежности нечёткого понятия «скорость движения ν около 130 км/ч».
Зависимость μ (ν), приведённая на рис.4.3, свидетельствует о том, что эксперт (лицо, принимающее решение) полагает возможным считать в заданных конкретных условиях значения ν = 100 … 160 км/ч соответствующими понятию «скорость движения ν около 130 км/ч», но значения, более близкие к ν = 130 км/ч, он считает более соответствующими данному понятию.
Это отображено на графике μ (ν) значениями μ, более близкими к единице. Вне указанных пределов лежат значения ν, не охваченные данным понятием, что формально отображается равенством μ (ν) = 0. Рассматриваемая оценка скорости ν может не иметь непосредственного отношения к фактическому распределению скоростей интересующего нас объекта.
Если возможны различные варианты нечётких множеств в пределах отображаемого нечёткого понятия, то такие варианты образуют нечёткую переменную. Так, нечёткая переменная может быть сформирована из различных оценок скорости движения, аналогичных представленной на рис.4.3.
Лингвистическая переменная является числовой характеристикой сложного понятия, определённого на множестве U и состоящего из ряда более простых понятий. Отображения последних называются термами и представляют собой нечёткие переменные, областью определения каждой из которых также является множество U. Так, если мы хотим оценить величину скорости движения с помощью понятий «малая», «средняя», «большая», то можем сделать это с помощью лингвистической переменной СКОРОСТЬ, содержащей три терма: МАЛАЯ, СРЕДНЯЯ и БОЛЬШАЯ. Эти термы должны перекрывать всю область определения скорости ν, которую мы определим в процентах (0 … 100%) от максимального значения скорости в интересующем нас диапазоне скоростей, хотя действительное значение ν может быть и больше. Будем считать, что малая скорость не может превышать на 50% максимальную, а большая скорость не может быть меньше 50%. Наиболее подходящим значением для средней скорости будем считать те же 50% от максимальной. В таком случае лингвистическая переменная СКОРОСТЬ может быть отображена, например, графиком, представленным на рис.4.4.
| μ |
| 1, 0 |
| 0, 5 |
| ν, % |
| М |
| С |
| Б |
Рис.4.4. Функция принадлежности лингвистической переменной СКОРОСТЬ:
М – МАЛАЯ, С – СРЕДНЯЯ, Б - БОЛЬШАЯ
Здесь имеются в виду абсолютные значения скорости, о которых можно говорить, когда направление движения не имеет значения. Примером такого движения может быть полёт самолёта при неизменной высоте полёта, неизменном атмосферном давлении и отсутствии ветра. В рассматриваемом случае значения ν < 0 невозможны, но значения ν > 100% вполне возможны, поскольку соответствуют понятию «большая», что отображаются значением μ = 1 при ν > 100%.
Нечёткие множества, соответствующие числовым значениям лингвистической переменной, называются нечёткими числами. Операции с нечёткими числами требуют введения понятия нечёткого отношения. Если имеются универсальные множества U и ν, состоящие из элементов u и ν, то нечётким отношением R (Relation) на множестве U x ν называется совокупность пар:
 , (4.36)
, (4.36)
где  – функция принадлежности нечёткого отношения, отображающая множество U x ν в единичный отрезок
– функция принадлежности нечёткого отношения, отображающая множество U x ν в единичный отрезок 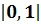 . Нечёткое отношение – это нечёткое множество с векторной базовой переменной.
. Нечёткое отношение – это нечёткое множество с векторной базовой переменной.
Нечёткие отношения дают численную характеристику таким высказываниям, как «Х много больше Y0» или «А значительно хуже В» и т.д. Истинность высказываний такого рода определяется не значениями U и ν в отдельности, а их соотношением. Соответственно и функция принадлежности  определяется совокупностью значений пары u, ν.
определяется совокупностью значений пары u, ν.
Арифметические операции над нечёткими числами производят в соответствии с принципом обобщения, который заключается в следующем. Пусть имеются два нечётких числа А и В, определённых на некотором интервале действительной оси. Пусть этим числом соответствуют носители: SA, заданный на интервале (a1, a2); SB, заданный на интервале (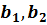 ).
).
Определим нечёткое число:
 •
• 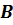 , (4.37)
, (4.37)
(где «•» - знак какой-либо из четырёх арифметических операций: +, ⎼, х, /) через функцию принадлежности:
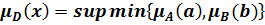 , (4.38)
, (4.38)
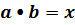 ,
,
где a и b – числа, принадлежащие соответственно носителям SA и SB.
Значение х определяется путём совершения заданной арифметической операции над числами a и b, а 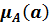 и
и 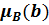 – это степени принадлежности чисел a и b в соответствии с функциями принадлежности нечётких множеств А и В.
– это степени принадлежности чисел a и b в соответствии с функциями принадлежности нечётких множеств А и В.
Очевидно, что путём подбора значений a и b можно получить одно и то же значение х для многих пар (a, b), которым будут соответствовать различные пары значений 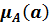 и
и 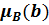 . Согласно соотношению (4.38) в каждой такой паре нужно выбрать меньшее (min) значение, а затем из всей совокупности полученных значений μ отобрать наибольшее (sup) значение, которое и будет искомым
. Согласно соотношению (4.38) в каждой такой паре нужно выбрать меньшее (min) значение, а затем из всей совокупности полученных значений μ отобрать наибольшее (sup) значение, которое и будет искомым  . Поскольку при определении степени принадлежности
. Поскольку при определении степени принадлежности  результата арифметической операции мы выбираем в каждой паре исходных значений μ меньшее значение, а в качестве окончательного значения
результата арифметической операции мы выбираем в каждой паре исходных значений μ меньшее значение, а в качестве окончательного значения 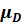 признаём наибольшее из выбранных меньших значений, то данный принцип обобщения называется максиминным, т.е. ориентированным на максимальный минимум значения μ.
признаём наибольшее из выбранных меньших значений, то данный принцип обобщения называется максиминным, т.е. ориентированным на максимальный минимум значения μ.
При обосновании принципа обобщения обратим внимание на то обстоятельство, что основой арифметических операций являются логические операции И (совпадения) (см. например, формулы (5.13) … (5.15)). Если трактовать степень принадлежности  как вероятность отнесения числа а к множеству А, а
как вероятность отнесения числа а к множеству А, а 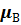 – как вероятность отнесения числа b к множеству В, то вероятность отнесения к множеству D результата произведённой над числами a и b арифметической операции будет близкой к произведению
– как вероятность отнесения числа b к множеству В, то вероятность отнесения к множеству D результата произведённой над числами a и b арифметической операции будет близкой к произведению  при условии, что процессы отнесения а к А и b к В независимы.
при условии, что процессы отнесения а к А и b к В независимы.
Обычно неизвестны ни распределения вероятностей на SA и SB, ни вид зависимости процессов отнесения аргументов a и b к нечётким числам А и В, приходится ограничиться максиминным соотношением (4.38). Его можно рассматривать как верхнюю оценку для  , которая тем точнее, чем больше различие значений
, которая тем точнее, чем больше различие значений 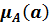 и
и 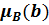 и чем полнее перебор пар a и b, таких что
и чем полнее перебор пар a и b, таких что 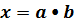 .
.
Пример 4.3. Выполнить сложение нечётких чисел А и В:
A = (0, 1/5; 0, 8/6; 0, 4/7);
B = (0, 2/4; 0, 9/5; 0, 3/6).
В знаменателе каждой реализации нечёткого числа стоит значение его носителя, а в числителе – степень принадлежности. Заданная арифметическая операция выполняется относительно всех возможных пар носителей. Минимальное значение суммы (А + В) равно 9; из исходных степеней принадлежности 0, 1 и 0, 2 выбираем меньшее. Следующее значение суммы равно 10. Оно может быть реализовано двумя способами: сложением 0, 1/5 и 0, 9/5 с минимальным значением μ А = 0, 1 и сложением 0, 8/6 с 0, 2/4 с минимальным значением μ В = 0, 2. В качестве μ А+В выбираем большее из меньших: μ А+В = 0, 2. Аналогичными рассуждениями приходим к окончательному результату:
А + В = (0, 1/9; 0, 2/10; 0, 8/11; 0, 4/12; 0, 3/13).
Пример 4.4. Выполнить умножение тех же нечётких чисел А и В, что и в примере 4.3.
Умножение, как и сложение, выполняется относительно всех возможных пар носителей, а результату умножения присваивается меньшая из двух степеней принадлежности. В результате получим:
АВ = (0, 1/20; 0, 2/24; 0, 1/25; 0, 2/28; 0, 8/30; 0, 4/35; 0, 3/36; 0, 3/42).
При выполнении операции умножения были получены два результата с носителем, равным 30: 0, 1/30 и 0, 8/30. В соответствии с максиминным принципом в окончательный результат вошло произведение 0, 8/30.
|
|