
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Спектры непериодических сигналов
|
|
Спектры непериодических сигналов конечной длительности (финитных) могут быть получены из уравнений для рядов Ф как предельные значения при 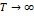 .
.
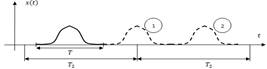
Зададим периодическую последовательность импульсов и разложим импульс на 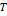 . Не меняя положения импульса на
. Не меняя положения импульса на 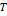 , увеличим значение
, увеличим значение 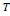 в два раза. При этом выражение для спектра останется без изменения, но число гармоник увеличится в два раза. Т.к.
в два раза. При этом выражение для спектра останется без изменения, но число гармоник увеличится в два раза. Т.к.  , т.е изменяем шаг дискретизации спектра по
, т.е изменяем шаг дискретизации спектра по 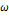 плюс за счет множителя
плюс за счет множителя 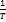 в два раза уменьшаются амплитуды гармоник.
в два раза уменьшаются амплитуды гармоник.
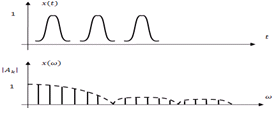

В пределе, при 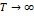 , периодическая последовательность импульсов заменяется одиночным финитным сигналом, дискретные частоты переходят в непрерывную последовательность
, периодическая последовательность импульсов заменяется одиночным финитным сигналом, дискретные частоты переходят в непрерывную последовательность 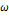 , а
, а 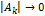 . Чтобы этого избежать, множитель
. Чтобы этого избежать, множитель 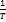 исключают, и мы приходим к интегралу Ф:
исключают, и мы приходим к интегралу Ф: 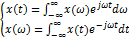
Спектр имеет смысл плотности спектра сигнала (спектральная функция сигнала)
Тригонометрическая форма интегр. Ф: 
Интегр. Ф существует для сигналов, удовлетворяющих условию Дирихле или
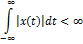
Если это условие не выполняется, то используют другие интегральные преобразования, в частности преобразование Лапласа. Пусть 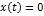 при
при 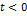 , а интеграл спектральной функции расходится. Тогда
, а интеграл спектральной функции расходится. Тогда 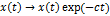 . Выберем
. Выберем 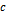 так, чтобы интеграл
так, чтобы интеграл 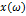 сходился, пользуемся
сходился, пользуемся
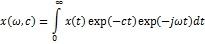
Требуем, чтобы 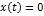 при
при 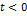 .
.
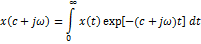
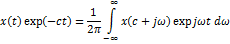
Умножая обе части на 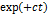 и заменяя переменную интегрирования
и заменяя переменную интегрирования 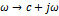 , получим тогда:
, получим тогда:
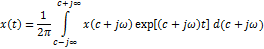
Обозначим 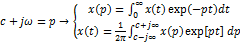
Получено преобразование Лапласа (оригинал + отображение)
Если вместо 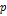 подставить
подставить 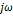 , то получим спектр Ф для Каузальных функций (т.е.=0 при
, то получим спектр Ф для Каузальных функций (т.е.=0 при 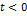 ).Итак, спектр непериодического сигнала
).Итак, спектр непериодического сигнала 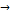 интеграл Ф:
интеграл Ф:

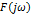 – комплексный амплитудно-частотный спектр
– комплексный амплитудно-частотный спектр
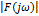 – амплитудный спектр
– амплитудный спектр 
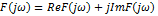
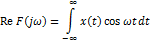
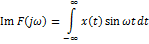
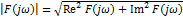
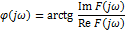
31(1). Спектральная плотность непериодических сигналов. Интегральное преобразование Фурье. Условия существования. Формы представления и свойства спектральной плотности.
Для характеристики стационарных в широком смысле случайных процессов в частотной области используется 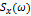 – спектральная плотность стационарного случайного процесса – преобразования Ф от корреляционной функции (в комплексной форме): – спектральная плотность стационарного случайного процесса – преобразования Ф от корреляционной функции (в комплексной форме):  Физический смысл
Физический смысл 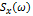 - разложение средней мощности случайного сигнала по частотам.
Спектральное разложение детерминированного непериодического сигнала называется преобразованием Ф. - разложение средней мощности случайного сигнала по частотам.
Спектральное разложение детерминированного непериодического сигнала называется преобразованием Ф.
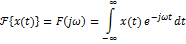
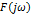 – комплексный амплитудный частотный спектр
| – комплексный амплитудный частотный спектр
| 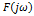 |- амплитудный спектр |- амплитудный спектр
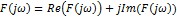
| 32.Основные свойства преобразования Фурье апериодических сигналов.
1. 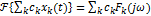 2.
2. 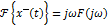
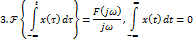 4.
4. 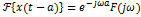 5.
5. 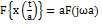 6.Преобразование свертки сигналов
6.Преобразование свертки сигналов

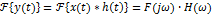 7.Преобразование произведения сигналов
7.Преобразование произведения сигналов
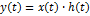
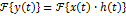
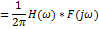 8.Спектр мощности сигналов
8.Спектр мощности сигналов
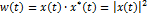
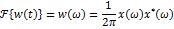
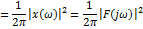 9.РавенствоПарсеваля
9.РавенствоПарсеваля 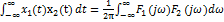
| 33.Мощность и энергия сигнала.
Спектр мощности сигналов
По определению, мощность сигнала есть
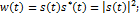
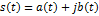
 Энергия сигнала:
Энергия сигнала:
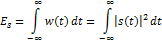 Средняя мощность на интервале
Средняя мощность на интервале 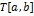 : :
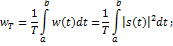 Связь энергии и нормы сигнала:
Связь энергии и нормы сигнала:
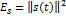 Энергия суммы сигналов:
Энергия суммы сигналов:
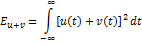
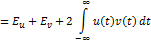
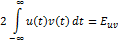
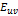 – энергия взаимодействия сигналов. – энергия взаимодействия сигналов. 
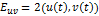 Спектр мощности сигналов
Спектр мощности сигналов
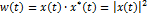
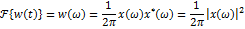
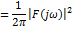 Равенство Парсеваля
Равенство Парсеваля
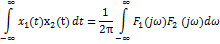
|
34(1). Спектры непериодических сигналов
Спектры непериодических сигналов конечной длительности (финитных) могут быть получены из уравнений для рядов Ф как предельные значения при 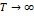 . .
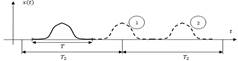 Зададим периодическую последовательность импульсов и разложим импульс на
Зададим периодическую последовательность импульсов и разложим импульс на 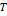 . Не меняя положения импульса на . Не меняя положения импульса на 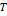 , увеличим значение , увеличим значение 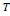 в два раза. При этом выражение для спектра останется без изменения, но число гармоник увеличится в два раза. Т.к. в два раза. При этом выражение для спектра останется без изменения, но число гармоник увеличится в два раза. Т.к.  , т.е изменяем шаг дискретизации спектра по , т.е изменяем шаг дискретизации спектра по 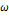 плюс за счет множителя плюс за счет множителя 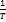 в два раза уменьшаются амплитуды гармоник. в два раза уменьшаются амплитуды гармоник.
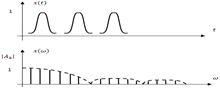
| ||
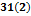
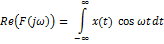
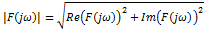
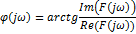 Свойства преобразования Ф.
1.
Свойства преобразования Ф.
1. 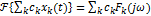 2.
2.  3.
3.  4.
4. 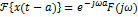 5.
5. 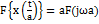 6.Теорема Парсеваля
6.Теорема Парсеваля
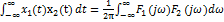
| ||
34(2).
 В пределе, при
В пределе, при 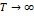 , периодическая последовательность импульсов заменяется одиночным финитным сигналом, дискретные частоты переходят в непрерывную последовательность , периодическая последовательность импульсов заменяется одиночным финитным сигналом, дискретные частоты переходят в непрерывную последовательность 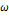 , а , а 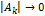 . Чтобы этого избежать, множитель . Чтобы этого избежать, множитель 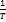 исключают, и мы приходим к интегралу Ф: исключают, и мы приходим к интегралу Ф: 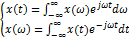 Спектр имеет смысл плотности спектра сигнала (спектральная функция сигнала)
Тригонометрическая форма интегр. Ф:
Спектр имеет смысл плотности спектра сигнала (спектральная функция сигнала)
Тригонометрическая форма интегр. Ф: 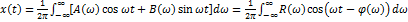 Интегр. Ф существует для сигналов, удовлетворяющих условию Дирихле или
Интегр. Ф существует для сигналов, удовлетворяющих условию Дирихле или
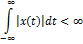 Если это условие не выполняется, то используют другие интегральные преобразования, в частности преобразование Лапласа. Пусть
Если это условие не выполняется, то используют другие интегральные преобразования, в частности преобразование Лапласа. Пусть 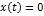 при при 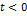 , а интеграл спектральной функции расходится. Тогда , а интеграл спектральной функции расходится. Тогда 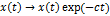 . Выберем . Выберем 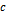 так, чтобы интеграл так, чтобы интеграл 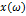 сходился, пользуемся сходился, пользуемся
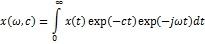 Требуем, чтобы
Требуем, чтобы 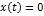 при при 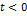 . .
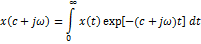
| 34(3)
 Умножая обе части на
Умножая обе части на 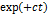 и заменяя переменную интегрирования и заменяя переменную интегрирования 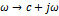 , получим тогда: , получим тогда:
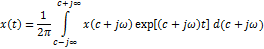 Обозначим
Обозначим 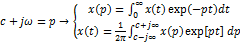 Получено преобразование Лапласа (оригинал + отображение)
Если вместо
Получено преобразование Лапласа (оригинал + отображение)
Если вместо 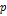 подставить подставить 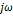 , то получим спектр Ф для Каузальных функций (т.е.=0 при , то получим спектр Ф для Каузальных функций (т.е.=0 при 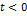 ).Итак, спектр непериодического сигнала ).Итак, спектр непериодического сигнала 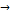 интеграл Ф: интеграл Ф:

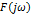 – комплексный амплитудно-частотный спектр – комплексный амплитудно-частотный спектр
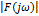 – амплитудный спектр – амплитудный спектр 
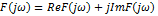
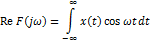
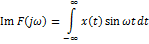
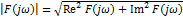
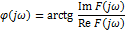
|
|
|