
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Число .
|
|
Покажем, что последовательность 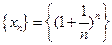 имеет предел. Для этого нодо показать, что она возрастающая и, что она ограничена сверху. Для преобразования
имеет предел. Для этого нодо показать, что она возрастающая и, что она ограничена сверху. Для преобразования  -го члена последовательности воспользуемся Биномом Ньютона:
-го члена последовательности воспользуемся Биномом Ньютона:

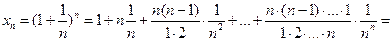

При увеличении  число слагаемых увеличивается, и каждое слагаемое увеличивается, значит, наша последовательность возрастающая. Далее имеем
число слагаемых увеличивается, и каждое слагаемое увеличивается, значит, наша последовательность возрастающая. Далее имеем
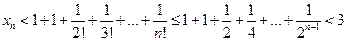 , т.е. наша последовательность ограничена сверху. В последнем выражении мы использовали неравенство
, т.е. наша последовательность ограничена сверху. В последнем выражении мы использовали неравенство 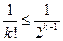 , которое можно доказать методом математической индукции, а также формулу суммы геометрической прогрессии. Таким образом, наша последовательность имеет предел, который назвали числом
, которое можно доказать методом математической индукции, а также формулу суммы геометрической прогрессии. Таким образом, наша последовательность имеет предел, который назвали числом 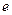 .
.
Пусть задана последовательность  . Выберем из нее бесконечное число элементов с номерами
. Выберем из нее бесконечное число элементов с номерами 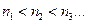 . Получим новую последовательность
. Получим новую последовательность  , которая называется подпоследовательностью последовательности
, которая называется подпоследовательностью последовательности  .
.
Теорема. (Больцано-Вейерштрасса). Из всякой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Доказательство. Так как  ограничена, то она принадлежит отрезку
ограничена, то она принадлежит отрезку  . Разделим его на две равные части. По крайней мере, один из них содержит бесконечное число элементов. Обозначим его через
. Разделим его на две равные части. По крайней мере, один из них содержит бесконечное число элементов. Обозначим его через 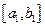 . Выберем какой-то элемент
. Выберем какой-то элемент 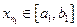 . Разделим
. Разделим 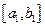 на две равные части, снова хотя бы один из них содержит бесконечное число элементов. Обозначим его
на две равные части, снова хотя бы один из них содержит бесконечное число элементов. Обозначим его  . Выберем какой-то элемент
. Выберем какой-то элемент 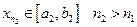 . Продолжим этот процесс. Получим систему вложенных отрезков и подпоследовательность
. Продолжим этот процесс. Получим систему вложенных отрезков и подпоследовательность  . Система вложенных отрезков стремится к нулю, следовательно имеет общую точку
. Система вложенных отрезков стремится к нулю, следовательно имеет общую точку 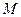 , к которой и сходится полученная подпоследовательность. Действительно
, к которой и сходится полученная подпоследовательность. Действительно  . Теорема доказана.
. Теорема доказана.
Теорема. (Критерий Коши). Для того чтобы последовательность сходилась (имела конечный предел) необходимо и достаточно чтобы она удовлетворяла условию Коши: 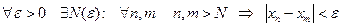 .
.
Доказательство. 1. (Необходимость). Пусть 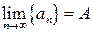 , тогда
, тогда  фундаментальна (удовлетворяет условию Коши).
фундаментальна (удовлетворяет условию Коши).
Имеем 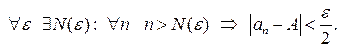 Пусть
Пусть  , тогда
, тогда 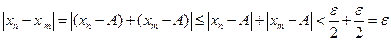 .
.
2. (Достаточность). Фундаментальная последовательность сходится (имеет конечный предел).
Сначала покажем, что фундаментальная последовательность ограничена. Пусть 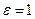 , тогда, согласно условию Коши,
, тогда, согласно условию Коши, 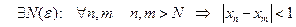 , в частности
, в частности 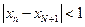 . Так как
. Так как 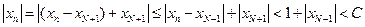 , где
, где 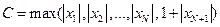 , последовательность ограничена.
, последовательность ограничена.
Согласно теореме Больцано-Вейерштрасса, из ограниченной последовательности можно выбрать сходящуюся подпоследовательность  .
.
Пусть 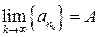 . Имеем
. Имеем 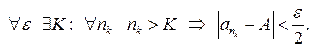
В силу фундаментальности этой последовательности 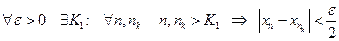 .
.
Если  , то
, то 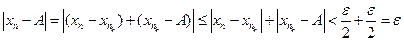 , то есть
, то есть 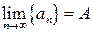 . Теорема доказана.
. Теорема доказана.
Пример. Покажем, что 
 расходится.
расходится.
Запишем отрицание к условию Коши: 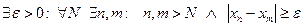 .
.
Пусть 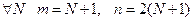 , тогда
, тогда 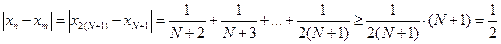 . Таким образом,
. Таким образом, 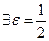 , при котором выполняется отрицание условия Коши.
, при котором выполняется отрицание условия Коши.
|
|