Понятие о геодезической линии, прямая геодезическая задача.

Таким образом, геодезическая линия является пространственной, а не плоской кривой или, иначе говоря, кривой двоякой кривизны. Наглядным аналогом геодезической линии может служить нить, туго натянутая между двумя точками поверхности сфероида.

Прямая геодезическая задача формулируется следующим образом: даны координаты некоторой начальной точки А, а также направление и расстояние от точки А к точке В. Необходимо определить координаты точки В.

При этом в геодезии всегда имеется в виду, что задано направление кратчайшей линии и минимальное расстояние между точками. В навигации в аналогичной задаче, называемой счислением пути, обычно подразумеваются заданными направление локсодромии и ее длина. Кроме того, в обеих интерпретациях, в зависимости от величины заданного расстояния S₀ и требуемой точности расчета координат φ ₁ и λ ₁, эта задача может решаться на эллипсоиде (с учетом сферичности Земли), на сфере или на плоскости.

При больших расстояниях между точками прямая геодезическая задача решается на эллипсоиде или сфере. В геодезии координаты пунктов и азимуты вычисляются с точностью до 0, 001΄. Это возможно лишь с учетом сфероидичности Земли на основе применения численных методов интегрирования системы уравнений (2.16)÷ (2.18). В судовождении, как правило, достаточная точность (до 0, 1') обеспечивается использованием формул сферической тригонометрии.

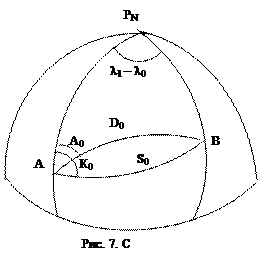
Рассмотрим сферический треугольник АРВ (рис.7), образованный дугами меридианов в начальной и конечной точек, равными90⁰-φ ₀ и 90⁰-φ ₁, а также соединяющей длиной D₀. Сферический угол при полюсе Р_N равен разности долгот λ ₁ – λ ₀, а угол между северной частью меридиана начальной точки и ортодромией равен А₀ (иногда его обозначают П₀ или 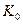). Известными являются величины φ ₀, λ ₀, Α ₀ и D₀.

Для определения широты φ ₁ можно воспользоваться теоремой косинуса стороны сферического треугольника, согласно которой

,

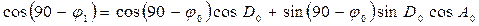откуда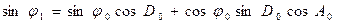

Долгота λ ₁может быть найдена как с использованием уже рассчитанной широты φ ₁, так и независимо от φ ₁. Рассмотрим независимое решение, которое выполняется с помощью теоремы котангенсов.

,

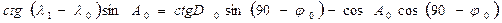откуда .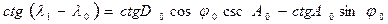

Для расчетов на калькуляторе эта формула преобразуется так, чтобы использовались только функции синуса, косинуса и тангенса:

.

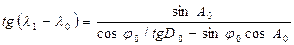В задаче счисления пути, близкой по сути к прямой геодезической задаче, заданы координаты начальной точки φ ₀ и λ ₀, направление пути 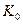и пройденное расстояние S₀. Определение координат φ ₁ и λ ₁ конечной (или текущей точки производится исходя из уравнений локсодромии на сфере где главные радиусы кривизны Ν 1 и Ν для любой точки поверхности равны радиусу сферы R (см. уравнения (23) и (24)):

; (2.24)

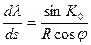. (2.25)

Интегрирование уравнения (2.24) не представляет затруднений, так как его правая часть является постоянной величиной

.

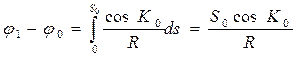Если расстояние Ѕ₀ выражено в морских милях, то разность широт по этой формуле получается в радианах. Для перехода к угловым минутам необходимо это значение разделить на arc1´, а так как R arc1´ =1, то разность широт в минутах находят по формуле

.

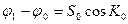Уравнение (32) содержит в правой части переменную величину φ. Интегрирование его можно выполнить по аналогии с выводом уравнения локсодромии (см. п.3.4.). В результате получается формула (2.21) с 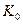вместо А и без второго слагаемого в квадратных скобках:

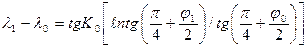(2.26)

При значениях 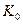близких к 90⁰ или 270⁰ этой формулой воспользоваться нельзя, т.к. tg 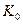-¥. Но при этом величина φ практически не изменяется. Считая φ постоянным, равным φ ₀, получаем следующее решение уравнения (2.25)

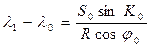
причем sin 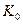= 1 при 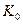= 90⁰ и sin 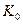= -1 при 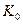= 270⁰.

Обе последние формулы дают разность долгот в радианах. Переход к угловым минутам производится делением этих значений на arc1´ =1/3437, 75, поэтому для практического использования эти формулы записываются в виде:

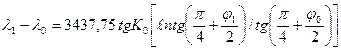(2.27)

при |K₀-90|≥ 1º и |K₀-270|≥ 1º;

λ ₁ – λ ₀ = S₀ / cosφ ₀ при |K₀-90|< 1º;

λ ₁ – λ ₀ = - S₀ / cosφ ₀ при |K₀-270|< 1º;

При малых расстояниях между начальной и конечной точками локсодромия и ортодромия практически сливаются в одну линию и рассмотренная задача в навигации обычно решается графически путем построения на карте.

7. Обратная геодезическая задача на сфероиде. Формулы Андуайе-Ламберта. Обратная геодезическая задача формулируется так: даны координаты точек А(φ ₀, λ ₀) и В(φ ₁, λ ₁); определить направление и расстоянию от А к точке В.

В большинстве случаев кратчайшее расстояние между двумя точками на поверхности Земли и направление кратчайшей линии можно рассчитать с достаточной для целей навигации точностью по формулам сферической тригонометрии. В сферическом треугольнике АР_Ν В (см. рис.7) при этом известны дуги меридианов, равные 90º - φ ₀ и 90º - φ _1, а также угол между ними, λ ₁ – λ ₀.

Ортодромическое расстояние D₀ находится по формуле косинуса стороны с учетом тождеств cos(90 - φ ₀) =sinφ ₀, sin(90 – φ ₀) = cosφ ₀ и т.п.:

cosD₀=sinφ ₀ sinφ ₁ + cosφ ₀ cosφ ₁ cos(λ ₁ – λ ₀). (2.28)

Если требуется повышенная точность определения кратчайшего расстояния между точками, то следует исправить величину D₀ поправкой за сфероидичность Земли, которую можно рассчитать по формуле Андуайе-Ламберта

, (2.29)

где ; .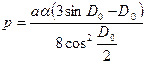

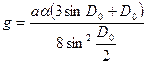В приведенной формуле величина D₀, не являющаяся аргументом тригонометрических функций, должна быть выражена в радианах. Величина Δ D получается в таких же единицах длины, в каких задана большая полуось 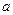земного сфероида. Если 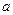- в метрах, то для представления Δ D в милях необходимо разделить результат на 1852.

Исправляемое расстояние D₀ относится к сфере с радиусом, равным 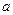. Поэтому расстояние D₀ (в милях) определяется как произведение угла D₀ (в радианах) на 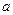(в милях). Длина геодезической линии D_Г = D₀ + Δ D.

Направление кратчайшей линии от точки А к точке В в навигационных задачах можно всегда считать совпадающим с направлением ортодромии и находить по формуле котангенсов

,

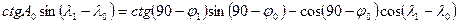откуда .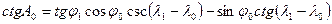

Для вычислений на калькуляторе эту формулу целесообразно представить в виде

.

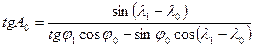В навигации существует задача расчета плавания по локсодромии, в которой по координатам двух точек требуется определить курс 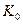и протяженность пути S₀ из одной точки в другую. Такая задача с достаточной точностью решается на основе полученных ранее уравнений локсодромии на сфере (см. формулы (2.27)¸ (2.29)).

Для нахождения локсодромического курса К₀ из точки А(j₀, l₀) в точку В(j₁, l₁) рассчитывается величина

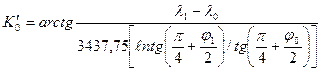, (2.30)

где разность долгот l₁ - l₀ выражается в угловых минутах.

Величина 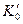находится в пределах от –90 до 90⁰. Переход от 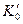к углу курса 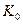производится исходя из соотношения широт и долгот начальной и конечной точек:

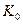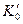= при j₁ > φ ₀; λ ₁ > 0;

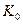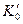= +180⁰ при j₁ < φ _0;

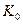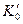= +360⁰ при j₁ > φ ₀; l₁ < l₀.

Если локсодромия пересекает меридиан, соответствующий λ = 180⁰, то во всех приведенных соотношениях нужно увеличить западную долготу на 360⁰. Например, если движется в западном направлении и λ ₀ = -170⁰, то нужно считать λ ₀ = 190⁰; если судно движется в восточном направлении иλ ₁ = -160⁰, то нужно принимать λ ₁ = 200⁰.

При j₀ = φ ₁ расчет по формуле (2.30) приводит к неопределенности, т.к. аргумент арктангенса стремится к бесконечности. В таких случаях локсодромический курс 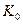с точностью до 0, 5⁰ принимается равным 90⁰ при движении судна на восток (l₁ > l₀) и 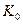= 270⁰ при движении на запад (l₁ < l₀).

Локсодромическое расстояние S₀ можно найти из уравнения (33) по известной разности широт j₁ - φ ₀ и рассчитанному курсу :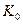

.

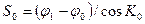Здесь j₁ - φ ₀ - в угловых минутах, а S₀ – в милях.

При 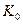близких к 90 или 270⁰ |cos 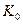| → 0 и при расчетах по формуле (35) и (36), вычислять S₀ по формуле

.

На основании сравнения локсодромического и ортодромического расстояния между заданными точками делается вывод о целесообразности плавания по ортодромии и выбирается более рациональный путь судна.

Основные понятия и определения математической картографии.

Географической картой называется уменьшенное обобщенное изображение земной поверхности на плоскости, полученное по определенному математическому закону.

Планом называется такое изображение земной поверхности на плоскости, искажения которого не выходят за пределы точности графических построений. Точность построения линейных величин при решении задач навигации принимается равной 0, 2 мм, а угловых – 0, 1⁰.

Частным масштабом карты называется отношение длины бесконечно малого отрезка ds на карте к длине соответствующего отрезка dS на местности:

Главным масштабом μ ₀ называется масштаб, указанный в заголовке карты. Обычно он равен частному масштабу в какой-либо особой точке или по определенной линии и приблизительно равен среднему значению частных масштабов данной карты. На советских картах знаменатель С₀ главного масштаба выражается круглым числом, заканчивающимся не менее чем тремя нулями, например, μ ₀ = 1/С₀ = 1: 100000.

В такой записи масштаб называется числовым или численным. Иногда используется линейный масштаб, который записывается, например, так: 10 км в 1 см или 5 миль в 1 см.

Масштаб плана во всех точках и по всем направлениям практически одинаков, поэтому он определяется как отношение длины любого отрезка S, взятого на плане, к длине соответствующего отрезка S на земной поверхности:

Увеличением (модулем) масштаба g называется отношение частного масштаба к главному:

g = μ / μ ₀ = С₀ / С.