Канонический вид квадратичной формы

Мы уже говорили о том, что в каждом базисе линейного пространства квадратичная форма задается однородным многочленом второй степени, который называется видом данной квадратичной формы.

Каноническим видом квадратичной формы называется такой ее вид, в котором коэффициенты при произведениях разноименных переменных равны 0, т. е. 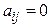при .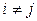

Нормальным видом действительной квадратичной формы называется такой ее канонический вид, в котором отличные от нуля коэффициенты при квадратах равны 1 или –1. Все отличные от нуля коэффициенты при квадратах нормального вида комплексной квадратичной формы равны 1.

Теорема 5.6. Для любой квадратичной формы, заданной на линейном пространстве в существует базис, в котором эта квадратичная форма имеет канонический вид, и существует базис, в котором она имеет нормальный вид.

Или другая формулировка этой же теоремы:

Для любой квадратичной формы от n переменных существует линейное невырожденное преобразование переменных, приводящее ее к каноническому виду, и существует линейное невырожденное преобразование переменных, приводящее ее к нормальному виду.

Теорему 5.6 мы докажем позже, а сейчас на примере покажем, как привести квадратичную форму к каноническому виду методом, который называется методом Лагранжа или выделения полных квадратов. Он заключается в следующем: выбираем переменную, коэффициент при квадрате которой отличен от 0, и выделяем полный квадрат, включающий в себя все слагаемые с этой переменной. С этой целью записываем перед скобкой число, обратное выбранному коэффициенту, а в скобках – половину производной по выбранной переменной. За скобками остается квадратичная форма, количество переменных которой уже на единицу меньше, с которой поступаем также. После конечного числа шагов получаем канонический вид.

Пример. ▼

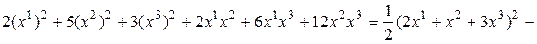
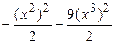
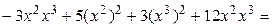
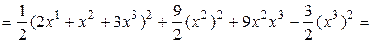
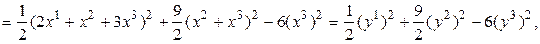
где 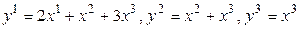. Матрица этого линейного преобразования запишется так:

.

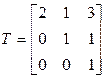Как видим, она невырождена, значит, и преобразование переменных является невырожденным. Вводя обозначения

,

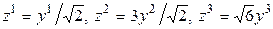получаем нормальный вид квадратичной формы: .▲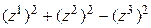

Замечания. 1. На самом деле при применении метода Лагранжа получаем не прямое преобразование, приводящее квадратичную форму к каноническому виду, а обратное, т. е. преобразование, которое выражает не старые переменные через новые, а наоборот.

2. Если все коэффициенты при квадратах исходной квадратичной формы равны нулю, а отличен от нуля, например, коэффициент при произведении 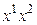, применим вначале следующее преобразование: 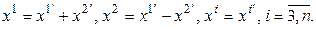Матрица этого преобразования выглядит так:

.

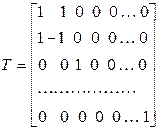Очевидно, она невырождена, и поэтому, соответствующее преобразование переменных также будет невырожденным.

Заметим, что канонический вид квадратичной формы определяется неоднозначно, тем не менее, имеет место

Теорема 5.7 (закон инерции). Все канонические виды одной квадратичной формы на действительном линейном пространстве имеют одинаковое число положительных коэффициентов и одинаковое число отрицательных коэффициентов. Нормальный вид квадратичной формы определяется однозначно с точностью до порядка следования коэффициентов.

► Доказательство достаточно провести для нормального вида.

Пусть в базисе 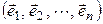линейного пространства квадратичная форма 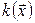имеет вид

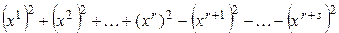, (5.21)

а в базисе 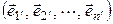– вид

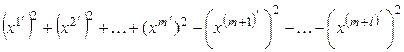. (5.22)

Так как 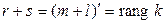, то достаточно показать, что 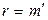. Предположим, что это не так. Пусть, например, 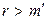. Обозначим

, .

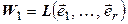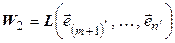Так как 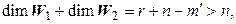а 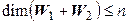, то сумма 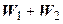не прямая, поэтому 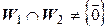, следовательно,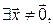 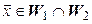. Так как 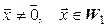, то из (5.21) видно, что 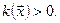Но так как 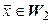, то из (5.22) видно, видно, что 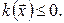Итак, мы пришли к противоречию. Таким образом, 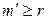. Аналогично доказывается, что 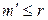, значит, .◄

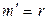Замечание. Для квадратичных форм на комплексном линейном пространстве нормальный вид, очевидно, определяется однозначно, так как количество отличных от нуля коэффициентов совпадает с рангом квадратичной формы.