
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Идентификация по протоколу Фиата-Шамира.
|
|
Схема его работы следующая. А доказывает В знание секрета s за t раундов по три сообщения в каждом.
Параметры протокола:
1. Доверительный центр Т выбирает и публикует модуль n (512-1024бита), являющийся произведением двух больших чисел (n=p*q, p и q сохраняются в секрете).
2. Каждый доказывающий выбирает секрет s взаимно простой с n,
1 ≤ s ≤ n-1, вычисляет v = s2 mod n и регистрирует v у Т в качестве своего открытого ключа.
Сообщения, передаваемые в рамках каждого раунда:
А → B: x = r2 mod n
B → A: e принадлежитмножеству {0, 1}
A→ B: y = rse mod n
B принимает доказательства за t раундов, и последовательность действий в рамках протокола имеет вид:
1. А выбирает случайное число r, 1 ≤ r ≤ n-1 и посылает В x=r2 mod n.
2. В выбирает случайным образом е и посылает его А.
3. А вычисляет y и посылает его В, где у = r при (e = 0) или y = r·s при (e =1).
4. B отвергает доказательство, если у = 0, иначе производится проверка
5. y2 ≡ xve (mod n). В зависимости от е у2 ≡ х2 mod n или y2 ≡ xv (mod n), иначе v ≡ s2 mod n.
Число раундов выбирается от 20 до 40.
Свойства нулевого разглашения относительно честного проверяющего может оказаться достаточно, если схема аутентификации используется, например, для контроля за доступом в охраняемое помещение. В этом случае абонент А – это пропуск, выполненный в виде интеллектуальной карточки, а B – компьютер охраны. В такой ситуации главная задача – обеспечить корректность схемы аутентификации, а защищаться от нечестного проверяющего бессмысленно. Что же касается свойства нулевого разглашения относительно честного проверяющего, то оно представляется далеко не лишним, так как позволяет обезопаситься от противника, который может попытаться подслушивать сеансы выполнения протокола с целью изготовления фальшивого пропуска.
Прежде чем завершить разговор о протоколах аутентификации необходимо подчеркнуть, что никакое математически строго доказанное свойство криптографического протокола не может гарантировать его безопасности во всех случаях жизни. В самом деле, даже протокол доказательства с нулевым разглашением не защищает от следующей атаки на схему аутентификации, известной в криптографической литературе под названием " мафиозная угроза''.
В данном сценарии имеются четыре участника: A, B, C и D. Предположим, что A зашел в кафе выпить чашечку кофе и расплачивается с помощью кредитной карточки. Для выполнения любой банковской операции карточка должна идентифицировать себя, т.е. выполнить протокол аутентификации. Но владелец кафе B – мафиози, сообщник которого C в тот же самый момент находится в магазине ювелира D и пытается купить бриллиант, также с помощью кредитной карточки. При этом C " представляется'' как A, а D просит доказать это с помощью протокола аутентификации. Устройство считывания для карточек у B и карточка у C – это специально изготовленные приемо-передающие устройства, которые лишь пересылают сообщения между A и D. В результате A, обмениваясь сообщениями с B, на самом деле идентифицирует себя для D.
Мы здесь не затрагиваем вопроса о практической осуществимости " мафиозной угрозы''. Мы привели ее просто как пример, показывающий, что только математического обоснования стойкости того или иного криптографического протокола недостаточно. Для практического применения конкретного протокола требуются еще усилия специалистов в области информационной безопасности по анализу условий его применения.
7. 2. Алгоритмы использования систем электронной цифровой подписи
При обмене информацией по коммуникационным сетям всегда стоит проблема подтверждения авторства сообщения и его целостности. Абонент А получает сообщение М от абонента В. Как подтвердить, что сообщение пришло именно от абонента В, а не сфальцифицировано злоумышленником или сообщение не подверглось искажению в процессе передачи по каналам связи.
Для подтверждения авторства и проверки целостности сообщений разработаны алгоритмы цифровой подписи. В основе большинства из них лежит идея использования односторонней функции с секретом Fs для создания пары (x, y), где x – сообщение, y – решение уравнения Fs(y) =x.
Имеем X – совокупность всевозможных сообщений, Y – некоторое множество " цифровых подписей". Пусть Fk: X ® Y – функция, зависящая от ключа k Î K. Ключ k состоит из двух частей ks и ko, где ks – секретная составляющая, известная только А, и ko – открытая составляющая (публикуется в открытом справочнике). Fk должна быть сюрьективной функцией, то есть для любого xÎ X существует прообраз y = Fk-1(x). Функция F считается общеизвестной и обладает следующими свойствами:
1. Зная ko, функцию Fk(y) можно вычислить по алгоритму за полиномиальное время.
2. Зная ks, функцию Fk(y) можно инвертировать по алгоритму полиномиальной сложности.
3. Зная ko, но не зная ks, функцию Fk(y) сложно инвертировать, то есть не известен или не существует полиномиальный алгоритм нахождения Fk-1(x).
Прообраз y = Fk-1(x) некоторого сообщения x называется подписью этого сообщения. Пара (x, y) называется подписанным сообщением.
В силу первого свойства всегда легко проверить, соответствует ли подпись сообщению, а в силу третьего – подделать подпись при достаточно большом ключе практически невозможно. Закрытый и открытый ключи находятся во взаимно – однозначном соответствии, и в силу третьего свойства нет полиномиального алгоритма вычисления секретного ключа по открытому.
На основании этих свойств можно сформулировать следующие требования к цифровой подписи:
1. Подпись должна быть битовым образцом, который зависит от подписываемого сообщения;
2. Подпись должна использовать некоторую уникальную информацию отправителя для предотвращения подделки или отказа;
3. Создавать цифровую подпись должно быть относительно легко;
4. Должно быть вычислительно невозможно подделать цифровую подпись как созданием нового сообщения для существующей цифровой подписи, так и созданием ложной цифровой подписи для некоторого сообщения;
5. Цифровая подпись должна быть достаточно компактной и не занимать много памяти.
В общем виде алгоритм ЭЦП выглядит следующим образом:
1. У отправителя А имеется закрытый ключ, а у получателя B – открытый.
2. Для передаваемого сообщения M отправитель А определяет значение Y = Fk-1(М).
3. Затем абонент А передает по каналу связи абоненту В пару (M, Y), где M – сообщение, а Y – подпись.
4. Получив подписанное сообщение (M, Y), В находит M' = Fk(Y). Знание открытого ключа позволяет сделать это за приемлемое время.
5. Получатель В сверяет M и M'. Если они совпадают, полученное сообщение считается подлинным. В противном случае либо сообщение M подверглось изменению, либо подпись Y неверна.
7.2.1. Схема ЭЦП Эль – Гамаля
Все пользователи знают большое простое число и примитивный элемент a Î (2, p -1) по модулю Р. Секретная информация подписывающего пользователя А состоит из двух частей:
1. XaÎ (2, p – 1) – долговременный секретный ключ подписи выбирается случайно из интервала (2, p – 1) и хранится в секрете.
2. KaÎ (1, p – 1) – разовый секретный ключ подписи конкретного сообщения, такой что НОД (Ka, p – 1) = 1, т.е. Ka взаимно просто с p -1.
Открытая информация подписывающего имеет 2 части:
1. ya = aXa(mod p) – открытый ключ подписи.
2. r = aKa (mod p) – первая из двух частей подписи (r, s).
Подписываемое сообщение представляется числом из интервала (0, p -1) точнее его функцией хэширования H(M).
Алгоритм подписи сообщения М:
1. Пользователь А выбирает случайное число Ka (секретный ключ подписи сообщения) из интервала (1, p − 1), таким образом, чтобы НОД (Ka, p – 1) = 1
2. Вычисляет Ka - 1(mod p - 1) – т.е. число удовлетворяющее сравнению Ka∙ xa ≡ 1(mod p - 1). Именно для разрешимости этого сравнения при выборе Ka наложено условие его простоты, с p - 1.
3. Вычисляем первую часть подписи r = aKa (mod p), которая не зависит от подписываемого сообщения и может быть вычислена заранее.
4. Вычисляем вторую часть подписи по формуле
s = Ka - 1[M – r∙ Xa] (mod p - 1).
На этом процедура выработки подписи (r, s) к сообщению М заканчивается, и эти данные M, r, s сообщаются получателям.
Алгоритм проверки подписи сообщения М:
По полученным M, r, s и имеющемуся у получателя открытому ключу отправителя ya вычисляются величины aM(mod p) и yar ∙ rs (mod p).
В случае выполнения равенства aM(mod p) = yar ∙ rs (mod p) считается, что подпись верная.
Поясним работу алгоритмов. Рассмотрим проверяемое равенство
aM(mod p) = yar ∙ rs (mod p) или сравнение aM ≡ yar ∙ rs (mod p) решением которого и является числа r и s.
После подстановки ya и r оно примет вид aM ≡ aXa∙ r ∙ aKa∙ s (mod p).
Учитывая свойства сравнений (теорема Эйлера - Ферма), последнее эквивалентно сравнение по модулю (p – 1) вида: M ≡ Xa∙ r + Ka∙ s (mod p – 1)
Именно из этого сравнения подписывающий пользователь вычисляет величину s ≡ Ka - 1 [M - Xa∙ r] (mod p – 1).
7.2.2. Применение алгоритма RSA для цифровой подписи
Система электронной подписи RSA получается при " смене мест" ключей e и d, т.е. обработка исходного сообщения для получения подписи производится с помощью закрытого ключа d. Цифровой подписью сообщения является число S = M d mоd (n), которое передается вместе с сообщением.
Проверка подлинности подписанного сообщения [M, S]: m =Se mod (n).
Равенство чисел принятого сообщения и расшифрованной подписи (M = m) доказывает, что сообщение M было подписано обладателем секретного ключа d, соответствующего ключу проверки подписи e, то есть происходит авторизация отправителя.
Протокол работы пары абонентов сети общей связи с алгоритмом RSA выглядит так.
1. Абоненты A (отправитель) и B (получатель) генерируют независимо друг от друга пары простых чисел: pa, qa и pb, qb
2. Вычисляют произведение больших простых чисел: na = pa * qa и nb = pb * qb
3. Вычисляют ключи: ea и da и eb и db
4. Числа na, nb и ea, eb помещаются в общедоступный справочник и получают статус открытых ключей; числа da, db сохраняются в качестве закрытых ключей;
5. Обмен зашифрованными сообщениями и формирование цифровой подписи:
5.1. Абоненты подписывают и шифруют сообщения:
А → Sa ≡ Ma da mоd(na);
c a ≡ M aeb mоd(nb);
В → Sb ≡ Mb db mоd(nb);
cb ≡ M bea mоd(na).
2. Передают А → В: Sa, ca;
В → А: Sb, cb;
3.Расшифровывают
А: Mb≡ cbda mоd(na),
В: Ma≡ cadb mоd(nb);
4. Проверяют подлинность подписи
В: ma≡ Saea mоd(na), А: mb≡ Sbeb mоd(nb)
В случае равенства значений принятых (Ma, Mb) и расшифрованных ma и mb сообщения считаются переданными без искажения, а пользователи А и В аутентифицированы.
8. ЭЛЕМЕНТЫ ТЕОРИИ РАВНОМЕРНО
РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Случайные числа играют важную роль при использовании криптографии, в частности для генерации ключей. К ним предъявляются два основных требования случайность и непредсказуемость.
Источники действительно случайных чисел найти трудно. Физические генераторы шумов, детекторы ионизирующей радиации, газовые разрядные трубки, имеющий утечку конденсатор иногда используются в качестве этих источников. Однако эти устройства в приложениях безопасности применяются ограниченно. Альтернативным решением является создание набора из большого числа случайных чисел и опубликование его в справочнике. Тем не менее, и такие наборы обеспечивают очень ограниченный источник чисел по сравнению с тем количеством, которое требуется в криптографических приложениях. Более того, хотя наборы из этих справочников действительно обеспечивает статистическую случайность, они предсказуемы, так как противник может получить их копию.
Исходя из изложенного, криптографические протоколы используют для создания случайных чисел специальные алгоритмы. Эти алгоритмы детерминированы и, следовательно, создают последовательность чисел, которая не является статистически случайной. Тем не менее, если алгоритм хороший, полученная последовательность будет проходить много тестов на случайность. Такие числа называют псевдослучайными числами.
Программный генератор равномерно распределенных случайных последовательностей (РРСП) – это программа для имитации на компьютере реализации РРСП с помощью псевдослучайной последовательности {xt}, которая:
1. Вычисляется по известному детерминированному рекурентному соотношению;
2. По статистическим свойствам не отличима от РРСП.
Имеется три основных подхода к построению алгоритмов генерации:
1. Прямые методы построения элементарных рекурентных последовательностей xt = f(xt-1, xt-2,..., xt-m): Am ® A.
2. Методы улучшения элементарных последовательностей, заключающиеся в специальных функциональных преобразованиях этих последовательностей для уменьшения отклонения их статистических свойств от свойств РРСП;
3. Комбинирование алгоритмов генерации, построенных с помощью первого или второго подхода.
8.1. Линейные регистры сдвига с обратной связью
Большинство реальных потоковых шифров основаны на линейных регистрах сдвига с обратной связью.
Линейным регистром сдвига с обратной связью (Linear Feedback Shift Register, сокращенно LFSR) называется логическое устройство, приведенное на рис. 8.1.
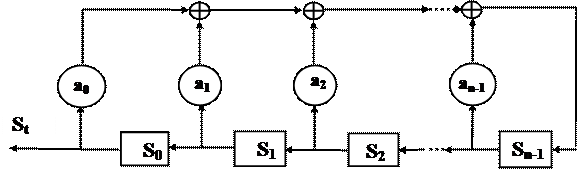 |
Рисунок 8.1 Блок – схема линейного регистра сдвига с обратной связью
Линейный регистр сдвига с обратной связью состоит из n ячеек памяти, двоичные состояния которых в момент времени t = 0, 1,... характеризуется значениями S0(t), S1(t),..., Sn-1(t), Î A ={0, 1}.
 Выходы ячеек памяти связаны не только последовательно друг с другом, но и с сумматорами в соответствии с коэффициентами передачи a0, a1,..., an-1 Î A, если ai = 1, то значение S1(t) i – й ячейки передается на один из входов i – го сумматора; если ai = 0, то такая передача отсутствует. Полагается a0 = 1. Состояние регистра сдвига в текущий момент времени t задается двоичным n - вектором S(t) = Sn-1(t), Sn-2(t),..., S0(t)).
Выходы ячеек памяти связаны не только последовательно друг с другом, но и с сумматорами в соответствии с коэффициентами передачи a0, a1,..., an-1 Î A, если ai = 1, то значение S1(t) i – й ячейки передается на один из входов i – го сумматора; если ai = 0, то такая передача отсутствует. Полагается a0 = 1. Состояние регистра сдвига в текущий момент времени t задается двоичным n - вектором S(t) = Sn-1(t), Sn-2(t),..., S0(t)).
Содержание ячеек регистра LFSR во времени изменяется следующим образом, определяя тем самым динамику своих состяний:
|
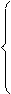 Si+1(t), если i Î {0, 1,..., n-2} (8.1)
Si+1(t), если i Î {0, 1,..., n-2} (8.1)
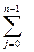 aj ∙ Sj(t), если i = n -1,
aj ∙ Sj(t), если i = n -1,
или в матричном виде:
 a0 a0
| a1 | a2 | ... | : | an-1 |
| In-1 | : | ||||
| : | : | ||||
| : |

где In-1 – единичная (n-1) ´ (n-1) – матрица, t = 0, 1,...
Текущие значения нулевой ячейки регистра используются в качестве элементов, порождаемой LFSR двоичной ПСП st = S0(t), которые с учетом (8.1) удовлетворяет линейному рекуррентному соотношению
st+n = 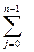 aj ∙ St+j, t = 0, 1,...
aj ∙ St+j, t = 0, 1,...
8.2. Линейные рекурентные последовательности
над конечными полями
Рекуррентные последовательности – это такие последовательности, каждый следующий член которых, начиная с некоторого, выражается по определенному правилу через предыдущие.
Определение. Пусть к - натуральное число, a, a0, a1,..., ak-1 – заданные элементы конечного поля Fq. Последовательность S0, S1,... элементов поля Fq, удовлетворяющая соотношению Sn+k = ak-1Sn+k-1 + ak-2Sn+k-2 +... + a0Sn + a, n = 1, 2,... называется линейной рекуррентной последовательностью (ЛРП) K - го порядка над полем Fq.
Первые члены S0, S1,... Sk-1 однозначно определяют всю последовательность и называются начальными значениями. Такое соотношение еще называют линейным рекуррентным соотношением K – го порядка.
Пример 49. Пусть порядок К = 4, тогда имеем линейную рекуррентную последовательность 4 порядка над полем Fq вида:
Sn+4 = a3Sn+3 + a2Sn+2 + a1Sn+1 + a0Sn + a. ▲
В практическом плане линейные рекуррентные последовательности реализуются на базе современных компьютерных систем, работающих на основе двузначной логики. Вся обработка информации осуществляется на основе элементов простого конечного поля F2 или его расширений F2N. Реализация линейных рекуррентных последовательностей над полем F2 может быть достаточно просто осуществлена на основе регистров сдвига с обратной связью. Пусть у нас имеется однородное линейное рекуррентное соотношение вида (т.е. порядка К=4): Sn+4 = a3Sn+3 + a2Sn+2 + a1Sn+1 + a0Sn, a0 = a1 = a2 = a3 = 1. Тогда его реализация на основе регистра сдвига из К=4 разрядов с обратной связью будет иметь вид:
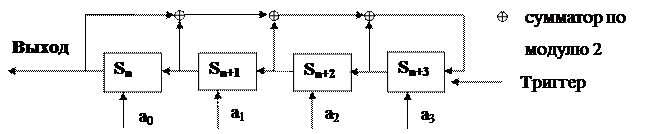
Рисунок 8.2 Регистр сдвига с обратной связью для К = 4
Под действием тактовых импульсов в моменты времени n = 1, 2,... на выходе регистра происходит генерация последовательности Sn, Sn+1, Sn+2,... Вектор
{Sn, Sn+1,..., Sn+k-1} – это вектор n - го состояния регистра. При n = 0 вектор
{S0, S1,..., Sk-1} – это вектор начального состояния.
Характерной особенностью линейных рекуррентных последовательностей над конечным полем является их периодичность, то есть повторная генерация состояний регистров.
Определение. Пусть S – произвольное непустое множество, и пусть S0, S1,... последовательность элементов из множества S. Если существуют целые числа r > 0 и n0 > 0, такие что, Sn+r = Sn для всех n ≥ n0, то последовательность S0, S1,... называется периодической последовательностью, а r - периодом этой последовательности.
Наименьший из всех возможных периодов называется минимальным периодом. Каждый период периодической последовательности делится на ее минимальный период. Для криптографических приложений желательно иметь линейную рекуррентную последовательность с максимальным периодом.
Линейные рекуррентные последовательности (ЛРП) над конечными полями тесно связаны с рассмотренными нами ранее многочленами.
Пусть S0, S1,... однородная ЛРП К – го порядка над полем Fq, удовлетворяющая рекуррентному соотношению:
Sn+k = ak-1Sn+k-1 + ak-2Sn+k-2 + a0Sn, (n = 0, 1, …) где aj Î Fq 0 ≤ j ≤ k-1. Многочлен вида f(x) = xk – ak-1xk-1 – ak-2xk-2 -...- a0 Î Fq[x] называется характеристическим многочленом данной ЛРП. Его вид зависит только от вида линейного рекуррентного соотношения.
Пример 50. Пусть ЛРП над полем F2 определяется соотношением
S n+2 = Sn+1 + Sn n = 0, 1,.... Тогда соответствующий ей характеристический многочлен имеет вид f(x) = x2 – x – 1. ▲
Существует прямая связь между периодом ЛРП и порядком характеристического многочлена.
Теорема. Пусть S0, S1,... – однородная ЛРП над полем Fq с ненулевым вектором начального состояния. Пусть ее характеристический многочлен
f(x) Î Fq[x] является неприводимым над полем Fq и удовлетворяет условию
f(0) ≠ 0. Тогда ЛРП S0, S1,... является чисто периодической последовательностью и ее минимальный период r = ord(f(x)).
Для практических приложений требуется формирование ЛРП с как можно большим минимальным периодом. Однородная линейная рекуррентная последовательность над полем Fq, характеристический многочлен, который является примитивным над этим полем Fq, а вектор начального состояния – ненулевым вектором, называется последовательностью максимального периода над полем Fq.
Теорема. Каждая последовательность К – го порядка максимального периода над полем Fq является чисто периодической последовательностью, а её максимальный период равняется qk - 1, наибольшему из возможных значений, которое может принимать минимальный период однородной ЛРП К - го порядка над полем Fq.
Пример 51. Имеется рекуррентное соотношение для однородной ЛРП над F2 вида: Sn+7 = Sn+4 + Sn+3 + Sn+2 + Sn n = 0, 1,...
Характеристический многочлен этой ЛРП имеет вид:
f(x) = x7 – x4 – x3 – x2 – 1 Î F2[x] и является примитивным над F2 то есть является нормированным неприводимым над F2 многочленом порядка
ord(f(x)) = 27 – 1 = 127.
Соответствующий регистр сдвига (LFSR) для заданного рекуррентного соотношения будет иметь вид, показанный на рисунке 8.3

Рисунок 8.3. LFSR для характеристического
многочлена f(x) = x7 – x4 – x3 – x2 – 1
Если в качестве вектора начального состояния регистра взять ненулевой элемент, то, согласно теореме, на его выходе получим последовательность S0, S1,... с минимальным периодом 127, т.е. все возможные 27 -1 ненулевые векторы встречаются в качестве векторов состояний этой последовательности. При разных начальных ненулевых векторах регистра получим разные ЛРП с одним и тем же периодом 127, но с некоторым сдвигом относительно друг друга. ▲
Вектор начального состояния регистра сдвига также можно представить в виде многочлена g(x) степени < К. Тогда, по сути дела, формирование ЛРП обусловлено процедурой деления многочленов g(x)/ f(x). Следует отметить, что из представленных выше результатов становится понятно, почему криптографы всего мира ищут неприводимые многочлены как можно более высокой степени К (так как r = 2k -1). Но эта задача и ее решение требует очень больших затрат. В связи с этим в теории конечного поля доказаны теоремы о том, что можно осуществлять операции почленного сложения или умножения линейных рекуррентных последовательностей, и таким образом увеличивать минимальный период ЛРП. Теорема. Пусть fi (i = 1, 2,..., h) – ЛРП над полем Fq. И пусть их минимальные периоды равны соответственно ri (i = 1, 2,..., h). Тогда если числа ri,..., rh попарно взаимно просты, то минимальный период произведения ЛРП f1, f2,..., fh равен произведению r1,..., rh.
Аналогично вводится операция суммирования ЛРП. При этом интересно отметить, что последний результат аналогичен и для операции сложения ЛРП:
Теорема. Пусть fi ЛРП над полем Fq (i = 1, 2,..., h). ri – их минимальные периоды. Тогда если числа ri попарно взаимно простые, то минимальный период суммарной последовательности f1 + f2 +...+ fh равен произведению r1· r2·...· rh.
Таким образом, суммирование и умножение ЛРП позволяет увеличить их минимальный период.
Для практических приложений весьма важным является вопрос о свойствах линейных рекуррентных последовательностей. Если суммировать все результаты, полученные при исследовании этого вопроса в рамках теории конечного поля и других прикладных дисциплин, то можно сказать следующие:
1. Наиболее важными и интересными свойствами обладают ЛРП максимального периода, формируемые характеристическими многочленами, являющиеся нормированными неприводимыми многочленами над соответствующими полями Fq.
2.ЛРП максимальной длины имеют равномерный спектр и, следовательно, статистическую равномерность.
3. Предельно большая длина периода qk - 1.
4. Отсутствие скрытой периодичности.
Отмеченные свойства делают ЛРП эффективным инструментом для создания генераторов псевдослучайных последовательностей, на базе которых строится широкий класс потоковых криптосистем.
В качестве примеров эффективно реализуемых на компьютере алгоритмов генерации вида приведем 4 генератора ПСП с периодом Tmax ≈ 296
xt+1 = (1176∙ xt + 1476∙ xt-2) mod(232 – 5)
xt+1 = 213(xt + xt-1 +xt-2) mod(232 – 5)
xt+1 = (1995∙ xt + 1998∙ xt-1 +2001∙ xt-2) mod(235 – 849)
xt+1 = 219(xt + xt-1 +xt-2) mod(235 – 1629)
8.3. Линейные и мультипликативные конгруэнтные генераторы
Линейным конгруэнтным генератором (ЛГК) с параметрами (x0, a, c, N) называется программный генератор РРСП, порождающий псевдослучайную последовательность (ПСП) x1, x2,...Î A, A = {0, 1,..., N – 1), с помощью рекурентного соотношения
xt+1 = (axt + c) mod N, t = 0, 1,... (8.2)
Параметры этого генератора (8.2) имеют следующий смысл: x0 Î A –начальное, или стартовое значение; a Î A – ненулевой множитель; c Î A –приращение; N - модуль, равный мощности алфавита A.
Если приращение c = 0, то генератор называется мультипликативным конгруэнтным генератором (МКГ), если c ¹ 0, то смешанным конгруэнтным генератором (СКГ).
Свойства пвседослучайной последовательности, порождаемой ЛКГ:
1. Для общего члена последовательности справедлива формула: xt = (atx0 + (at – 1))/ ((a -1)∙ c) mod N, t ³ 1.
2. Найдется номер τ Î A, начиная с которого последовательность (8.2) зацикливается, то есть она имеет период повторения равный T ≤ N – τ.
3. Для любого k ³ 2 подпоследовательность x0, xk, x2k, x3k,...Î A, полученная из псеводслучайной последовательности (8.2) удалением всех членов, некратных k, оказывается псевдослучайной последовательностью, порожденной ЛКГ (8.2), с параметрами (x0, a', c', N), где a' = ak mod N, c' = ((ak -1))/((a – 1)∙ c) mod N.
4. Псевдослучайная последовательность (8.2), порождаемая ЛКГ, достигает максимального значения периода Tmax = N (τ = 0) тогда и только тогда, когда выполнены следующие три условия:
а) c и N – взаимно простые;
б) число b = a -1 кратно p для любого простого числа p < N, являющегося делителем N;
в) число b кратно 4, если N кратно 4.
5. Для МКГ, (c = 0), если x0 и N взаимно простые, a – первообразный элемент по модулю N, а φ (N) – максимально возможный порядок по модулю N, то псевдослучайная последовательность имеет максимальный период Tmax = φ (N).
6. Для МКГ, если N = 10q, q ³ 5 и x0 не кратно 2 или 5, то максимально возможное значение периода Tmax = 5 * 10q-2 = N/20 псевдослучайной последовательности достигается тогда и только тогда, когда вычет a (mod 200) принимает одно из 32 следующих " магических" значений: 3, 11, 13, 19, 21, 27, 29, 37, 53, 59, 61, 67, 69, 77, 83, 91, 109, 117, 123, 131, 133, 139, 141, 147, 163, 171, 173, 179, 181, 187, 189, 197.
7. Для МКГ, если N = 2q, q ³ 4, то максимально возможное значение периода Tmax = 2q-2 = N/4 псевдослучайной последовательности достигается если, x0 ³ 1 – нечетно и вычет a (mod 8) Î {3, 5}.
8. Для МКГ, если x0 ¹ 0, N – простое число и справедливо разложение на множители: N – 1 = p1m1 ∙ ∙ ∙ psms, где p1,..., ps – простые числа, то максимально возможное значение периода Tmax = N -1 псевдослучайной последовательности достигается для случая, когда
 a(N – 1)/pj ¹ 1 (mod N), j = 1, s.
a(N – 1)/pj ¹ 1 (mod N), j = 1, s.
9. " Слабость" ЛКГ и МКГ заключается в том, что если рассматривать последовательные биграммы (z1(t), z2(t)): z1(t) = xt, z2(t) = xt-1, то точки на плоскости R2 будут лежать на прямых из семейства z2 = az1 + c – kN, k = 0, 1,...
8.4. Нелинейные конгруэнтные генераторы
Свойство 9 ЛКГ и МКГ может активно использоваться для построения криптоатак в целях оценки параметров a, c, x0. Для устранения этого недостатка используют нелинейные конгруэнтные генераторы псевдослучайных последовательностей, среди которых известны: квадратичный конгруэнтный генератор; генератор Эйхенауэра-Лена с обращением; конгруэнтный генератор, использующий умножение с переносом; квадратичный генератор Ковэю; генератор " середины квадрата" и др.
8.4.1. Квадратичный конгруэнтный генератор
Алгоритм генерации ПСП xt Î A = {0, 1,..., N-1} определяется квадратичным рекурентным соотношением
xt+1 =(dxt2 + axt + c) mod N, t = 0, 1,..., (8.3)
где x0, a, c, d Î A – параметры генератора. Выбор этих параметров осуществляется на основе следующих двух свойств последовательности (8.3):
1. Квадратичная конгруэнтная последовательность имеет наибольший период Tmax = N тогда и только тогда, когда выполнены следующие условия:
а) c и N – взаимно простые числа;
б) d, a – 1 – кратны p, где p – любой нечетный простой делитель N;
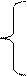 в) d – четное число, причем
в) d – четное число, причем
|
(a – 1) mod 2, если N кратно 2;
г) если N кратно 9, то либо d mod 9 = 0, либо d mod 9 = 1 и с∙ d mod 9 = 0
2. Если N = 2q, q ³ 2, то наибольший период Tmax = 2q тогда и только тогда, когда с – нечетно, d – четно, a – нечетное число удовлетворяющее соотношению a = (d + 1) mod 4.
8.4.2. Генератор Эйхенауэра-Лена с обращением
Псевдослучайная нелинейная конгруэнтная последовательность Эйхенауэра-Лена с обращением определяется следующим нелинейным рекурентным соотношением (t = 0, 1, 2,...):
|
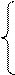 (axt-1 + c) mod N, если xt ³ 1, (8.4)
(axt-1 + c) mod N, если xt ³ 1, (8.4)
c, если xt = 0
где xt-1Î A – обратный к xt элемент по модулю N, то есть xt xt-1 ≡ 1(mod N); x0, a, c Î A – параметры генератора.
Если N = 2q, a, x0 – нечетны, с – четно, то генератор имеет максимально возможный период Tmax = 2q-1 тогда и только тогда, когда a ≡ 1 (mod 4), c ≡ 2 (mod 4).
8.4.3. Конгруэнтный генератор, использующий умножение с переносом
При этом нелинейная псевдослучайная последовательность определяется рекурентным соотношением xt+1 = (axt + ct) mod N, t = 0, 1,...
где приращение ct = c(xt-1, xt-2,..., x0) изменяется во времени и зависит от указанных аргументов нелинейно:



 сt = (axt-1 + ct-1)/ N
сt = (axt-1 + ct-1)/ N
8.5. Криптостойкие генераторы на основе односторонних функций
Для повышения стойкости алгоритмов генерации ПСП к криптоанализу предлагается синтезировать алгоритмы на основе односторонних функций. Характерное свойство односторонних функций состоит в том, что для вычисления значения функции по заданному значению аргумента существует полиномиально сложный алгоритм, в то же время как для вычисления аргумента по заданному значению функции полиномиально сложного алгоритма не существует (или он неизвестен).
8.5.1. Генератор ANSI X9.17
Представляет собой национальный стандартный алгоритм США для генерации двоичной ПСП, входящейв FIPS (USA Federal Information Processing Standart). В этом генераторе в качестве односторонней функции используетсмя тройной DES с двумя ключами K1, K2 Î V64 – это алгоритм шифрования вида:
FK = EK1 ∙ DK2 ∙ EK1,
где K = (K1||K2) Î V128 – составной 128 – битовый ключ. EK1 – алгоритм шифрования DES с ключом K1; DK2 -алгоритм расшифрования DES с ключом K2 ¹ K1.
8.5.2. Генераторы FIPS – 186
Они также являются национальным стандартом США и предназначены для генерации конфиденциальных параметров и ключевой информации для алгоритма электронной цифровой подписи DSA. В качестве односторонней функции используется алгоритм шифрования DES или алгоритм хеширования SHA -1.
Список рекомендуемой литературы:
1. Ю. С. Харин, В.И. Берник, Г.В.Матвеев, С.В. Агиевич " Математические и компьютерные основы криптологии", Минск, ООО" Новое знание", 2003г.
2. В.М. Фомичев " Дискретная математика и криптология", М., " Диалог-МИФИ", 2003г.
3. А.Г. Ростовцев, Е.Б. Маховенко " Теоретическая криптография", Санкт-Петербург, НПО " Профессионал", 2005г.
4. Н.А. Молдовян " Практикум по криптосистемам с открытым ключом", Санкт - Петербург, " БХВ – Петербург", 2007г.
5. Нильс Фергюсон, Брюс Шнайер " Практическая криптография". Пер. с англ. – М. Издательский дом " Вильямс", 2005 г.
|
|