
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Бинарные отношения 3 страница
|
|
В случае F Ì P говорят также, что поле P является расширением своего подполя F. Из определения подполя следует, что ноль и единица поля P будут содержаться также в F и служить для F нулем и единицей. Если взять в P пересечение F1 всех подполей, содержащих F и некоторый элемент a Î P, не принадлежащий F, то F1 будет минимальным полем, содержащим множество {F, a}. Говорят, что расширение F1 поля F получено присоединением к F элемента a, и отражают этот факт в записи F1=F(a).
Аналогично можно говорить о подполе F1 = F(a1, …an) поля P, полученном присоединением к F n элементов a 1, … a n поля P.
Поля P и P' называются изоморфными, если они изоморфны как кольца. По определению f (0)=0' и f (1)=1' для любого изоморфного отображения f. Не имеет смысла говорить о гомоморфизмах полей, так как Ker f ≠ 0 Þ f(a) = 0, a ≠ 0 Þ f(1) = f(a∙ a-1) = f(a) ∙ f(a-1)=0∙ f(a-1) = 0 Þ f(b) = f(1∙ b) = 0∙ f(b) = 0 " b Þ Ker f = P. Напротив, автоморфизмы, т.е. изоморфные отображения поля P на себя, связаны с самыми глубокими свойствами полей и являются мощным инструментом для изучения этих свойств.
2.7.2. Поле Галуа
Поле К называется конечным, или полем Галуа, если оно состоит из конечного числа элементов.
Теорема. Кольцо классов вычетов Zm с элементами 0, 1,..., m-1 будет областью целостности, а значит и полем, лишь при простом m.
Именно конечное кольцо классов вычетов Zp и называется полем Галуа порядка p и обозначается через Fp или GF(p). Характеристика поля GF(p) равна p.
Образующим элементом q поля GF(p) называется элемент порядка
p-1. (Это равносильно тому, что степени q пробегают все элементы GF(p).
Всего в GF(p) имеется φ (p-1) различных образующих элементов,
где φ (p) – функция Эйлера.
Если q – образующий элемент поля GF(p), то qj является корнем n -ой степени из единицы тогда и только тогда, когда n∙ j ≡ 0(mod p-1). Число корней n -ой степени из единицы равно НОД(n, p-1). В частности, GF(p) содержит так называемый примитивный корень n -ой степени из единицы (т.е. такой элемент ψ, что степени ψ пробегают все корни n -ой степени из единицы), тогда и только тогда, когда n|p-1. Если ψ - примитивный корень n -ой степени из единицы в GF(p), то ψ j – также примитивный корень n -ой степени из единицы, если НОД(n, j) = 1.
Квадраты в GF(p) – называются квадратичными вычетами. Остальные элементы называются невычетами. В GF(p) имеется ровно (p-1)/2 квадратичных вычетов и невычетов
Пример 24. Пусть p = 11. Тогда квадратичными вычетами в GF(11) будут следующие числа: 12 = 1; 22 = 4; 32 = 9; 42 = 5; 52 = 3; 62 = 3; 72 = 5; 82 = 9; 92 = 4; 102 = 1, т.е. числа 1, 3, 4, 5, 9. Невычетами будут числа 2, 6, 7, 8, 10. ▲
Среди квадратичных вычетов присутствуют числа, являющиеся обычными квадратами в Z. В примере это 22=4, 32=9. Числа 2 и 4 называются главными квадратичными корнями.
Пусть F – конечное поле, содержащее подполе К из q элементов. Тогда F состоит из qm элементов, где m = [F: K].
Здесь [F: K] обозначает степень поля F над К, т.е. размерность пространства F над К, если рассматривать F как векторное пространство над полем К.
Теорема. Пусть F – конечное поле. Тогда оно состоит из рn элементов, где р простое число, являющееся характеристикой поля F, а n – натуральное число, являющееся степенью поля F над его простым подполем.
Если F – конечное поле из q элементов, то каждый элемент а Î F удовлетворяет равенству аq = а .
3. КОЛЬЦО МНОГОЧЛЕНОВ
3.1. Основные понятия и определения
Многочленом (или полиномом) степени n над полем P, от переменной x – называется выражение вида
f(x) = f0 + f1x + f2x2 +... + fnxn; (3.1)
где fk (k = 0, 1,..., n) являются элементами поля P (называются коэффициентами многочлена), причем fn ≠ 0 (этот коэффициент называется старшим);
n – степень многочлена, обозначаемая deg f(x).
Многочлены степени n = 0, то есть ненулевые элементы поля P, называются постоянными.
Краткая запись многочленов: f(x) = 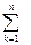 fkxk; fn ≠ 0.
fkxk; fn ≠ 0.
Множество всех многочленов над полем P, от переменной x, обозначается P[x].
Наряду с записью многочлена f(x) Î P[x] в порядке возрастания степеней (3.1) в практических приложениях применяется запись в порядке убывания степеней:
f(x) = a0 xn+ a1xn-1 + a2xn-2 +...+an-1x + an; ak Î P (k = 0, 1,..., n); a0 ≠ 0.
Два многочлена f(x) и g(x) (над одним тем полем P и от одной и той же переменной x) называются равными f(x) = g(x), если:
1. их степени одинаковы;
2. все соответствующие коэффициенты равны.
Для многочленов, также как и для чисел, могут быть введены арифметические операции.
Сумма многочленов f(x) и g (x) определяется равенством
hk = fk + gk (k = 0, 1, 2,...) (3.2)
Это означает, что при сложении многочленов складываются их коэффициенты при соответствующих степенях.
Операция умножения определяется как:
fi ∙ gj = hk = (h0, h1, h2, …), (3.3)
где hk = 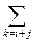 fi ∙ gj, k = 0, 1, 2, …
fi ∙ gj, k = 0, 1, 2, …
Ясно, что в результате сложения и умножения получится снова последовательность вида (3.1) с конечным числом отличных от нуля членов.
Пример 25. Сумма и произведение многочленов
a(t)+b(t)=(a0+a1∙ t+a2∙ t2)+(b0+b1∙ t+b2∙ t2)=(a0+b0)+(a1+b1)∙ t+(a2+b2)∙ t2.
a(t) ∙ b(t)=a0∙ b0+(a0b1+a1b0)∙ t+(a0b2+a1b1+a2b0)∙ t2+(a1b2+a2b1)∙ t3+a2b2∙ t4. ▲
Существует теорема, которая гласит, что если f (x) и g (x) многочлены, тогда
deg(f(x) + g(x)) ≤ max (deg(f(x)); deg(g(x))); (3.4)
deg(f(x) ´ g(x)) = (deg(f(x)) + deg(g(x)); (3.5)
причем, если deg(f(x)) ≠ deg(g(x)), то неравенство (3.4) обращается в равенство.
Многочлен f(х) делится на многочлен g (x), если существует многочлен q (x) такой, что f (x) = q (x)· g (x).
В этом случае говорят, что многочлен g (x) делит многочлен f (x), при этом g (x) – делитель многочлена f (x), а f (x) – кратное многочлена g (x).
Для многочлена f(x) = a0 + a1x +…+ anxn коэффициент а0 является постоянным членом то есть константой.
Пример 26. Так как в компьютерах используется двоичная система счисления, рассмотрим поле Галуа, состоящее из элементов {0, 1}, действия над которыми выполняются по модулю 2 (это самое маленькое из конечных полей). Обозначение GF(2N) соответствует строкам данных длиной N бит. Такие строки бит удобно рассматривать в виде многочленов. Например, байт можно представить в следующем виде (10010101) = x7 + x4 + x2 + 1.
Перечислим все многочлены степени не выше трех над этим полем.
(F2)3[x] = {0; 1; x; x + 1; x2; x2 + 1; x2 + x; x2 + x + 1; x3; x3 + 1; x3 + x; x3 + x + 1; x3 + x2; x3 + x2 + 1; x3 + x2 + x; x3 + x2 + x + 1}. ▲
Обратите внимание, что хотя данное поле является конечным, множество всех многочленов над этим полем будет бесконечным.
Теорема. Множество P[x] многочленов над полем P с алгебраическими действиями сложения и умножения, заданные формулами (3.2 и 3.3), является коммутативным кольцом.
Доказательство. Выполнение требований по сложению очевидно. Мы уже рассмотрели сложение коэффициентов, которое выполняется в кольце. Нулем кольца многочленов является многочлен с нулевыми коэффициентами. Дистрибутивность следует из равенства: 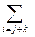 aj(bk + ck) =
aj(bk + ck) = 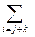 ajbk +
ajbk + 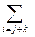 ajck.
ajck.
 Ассоциативность умножения следует из равенства для коэффициентов:
Ассоциативность умножения следует из равенства для коэффициентов:
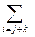 ak·
ak· 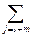 blcm =
blcm = 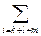 akblcm
akblcm
Кольцо многочленов над R обозначается R[x]. Многочлены степени 0 являются элементами кольца R, поэтому кольцо многочленов содержит R. Переход от R к R[x] называется присоединением переменной x к кольцу R.
Пример 27. Рассмотрим два многочлена над полем F5 классов вычетов по модулю 5: f(x) = 4x2 + x + 3; g(x) = x2 + 2x + 2.
Выполним алгебраические действия сложения, вычитания и умножения над этими многочленами: f(x) + g(x) = 3x;
f(x) - g(x) = 3x2 + 4x + 1;
(4x2 + x + 3)´ (x2 + 2x + 2) = 4x4 + 4x3 + 3x2 + 3x + 1. ▲
3.2. Разложение в кольце многочленов
Теорема. Пусть m1,..., mr – попарно взаимно простые числа (т.е. НОД(m1, mr) = 1 и m = m1· m2·...·mr. Тогда справедливо:
1. Сравнение f(x) ≡ 0(mod m) равносильно системе сравнений
f(x) ≡ 0(mod m1);
f(x) ≡ 0(mod m2);
...;
f(x) ≡ 0(mod mr)
2. Число решений сравнения f(x) ≡ 0(mod m) равно произведению числа решений отдельных сравнений, указанной в п.1. системы сравнений.
По аналогии с целыми числами можно ввести понятия наибольшего общего делителя многочленов, наименьшего общего кратного многочленов, взаимно простых и попарно взаимно простых многочленов, отношение сравнимости многочленов и ряд других важнейших понятий.
Теорема. Пусть f1(x),..., fn(x) – многочлены, не все равные нулю. Тогда существует однозначно определенный нормативный многочлен d(x), обладающий свойствами:
1. d(x) делит каждый многочлен fi(x), i = 1,..., n.
2. Любой многочлен g(x), который делит каждый из многочленов fi(x), i = 1,..., n, делит и многочлен d(x).
Нормированный многочлен d(x) называют наибольшим общим делителем многочленов f1(x),..., fn(x) и обозначают НОД(f1(x),..., fn(x)). Если НОД(f1(x),..., fn(x)) = 1, то многочлены f1(x),..., fn(x) являются взаимнопростыми. Многочлены называются попарно взаимно простыми, если
НОД(fi(x), fj(x)) = 1; для всех 1 ≤ i < j ≤ n.
Наибольший общий делитель двух многочленов (также как и двух целых чисел) можно найти при помощи алгоритма Евклида. Пусть многочлен g(x) ¹ 0 и не делит многочлен f(x).
Тогда, применяя многократно алгоритм деления многочленов с остатком, получим:
f(x) = g1(x)·g(x) + r1(x) 0 ≤ deg (r1(x)) < deg (g(x))
g(x) = g2(x)·r1(x) + r2(x) 0 ≤ deg (r2(x)) < deg (r1(x))
r1(x) = g3(x)·r2(x) + r3(x) 0 ≤ deg (r3(x)) < deg (r2(x))
· · ·
rs-2(x) = gs(x)·rs-1(x) + rs(x) 0 ≤ deg (rs(x)) < deg (rs-1(x))
rs-1(x) = gs+1(x)·rs(x)
Т.к. степень deg(g(x)) конечна, то процедура заканчивается за конечное число шагов. Если старший коэффициент последнего ненулевого остатка rs(x) равен b, то НОД(f(x), g(x)) = b-1·rs (x).
Пример 28. Найти НОД по алгоритму Евклида следующих многочленов над полем F2:
f(x) = x6 + x3 + x2 + 1
g(x) = x4 + x2 + x
x6 + x3 + x2 + 1 = (x2 - 1)·(x4 + x2 + x) + x +1
x4 + x2 + x = (x3 - x2 +1)·(x + 1) + 1
x + 1 = (x + 1)· 1
Значит, НОД(f(x), g(x)) = 1 то есть многочлены f(x) и g(x) взаимно простые. ▲
3.3. Неприводимые многочлены
Многочлен f(x) ненулевой степени из кольца R [ X ] называется неприводимым в R [ X ] (или неприводимым над полем P), если он не делится ни на какой многочлен g Î R[X], у которого 0 < deg g(x) < deg f(x). В частности, всякий многочлен первой степени неприводим. Совершенно очевидно, что неприводимость многочлена степени > 1 или разложение его на простые множители – понятия, тесно связанные с основным полем P. Как простых чисел в Z, так и унитарных неприводимых многочленов над произвольным полем P бесконечно много.
Так как над конечным полем количество многочленов заданной степени ограничено, то можно сделать следующее полезное заключение: над любым конечным полем существуют неприводимые многочлены сколь угодно высокой степени.
А теперь приведем без доказательства к ритерий неприводимости:
пусть f(x) = xn + a1 xn-1 +…+ an-1 x + an Î Z[x] – унитарный многочлен над Z, все коэффициенты a1, …, an которого делятся на некоторое простое число p, но an не делится на p2. Тогда f[x] неприводим над Q (множеством рациональных чисел).
Примечание.Критерий действует и в том случае, когда старший коэффициент отличен от 1, но не делится на p.
Многочлен положительной степени f(x) называется приводимым, если существуют два многочлена положительной степени f1(x) и f2(x) такие, что f(x) = f1(x)·f2(x), т.е. если этот многочлен f(x) не является неприводимым.
Неприводимые многочлены играют важную роль в теории чисел, так как любой многочлен f(x) может быть записан, причем единственным способом, в виде произведения неприводимых многочленов (аналог того, что любое число n > 1 может быть представлено в виде произведения простых чисел).
Теорема. (Об однозначном разложении на множители)
Каждый многочлен положительной степени f(x) может быть представлен в виде произведения f(x) = a·f1m1(x)·...·fnmn(x),
где а - старший коэффициент f(x);
f1(x),..., fn – различные нормированные неприводимые многочлены;
m1,...mn – натуральные числа 1, 2, ….
При этом такое разложение называют каноническим разложением многочлена.
В криптосистемах особенный интерес представляют неприводимые многочлены степени n над простыми полями Fp порядка p, где p – простое число. Поиск всех неприводимых многочленов заданной степени n над некоторым полем Fp представляет собой очень сложную задачу. Французский математик Эварист Галуа (1811 -1832гг) создал теорию (теорию поля Галуа), доказывающую существование неприводимых многочленов сколь угодно большой степени, но поиск таких многочленов – очень сложная задача, и криптографические службы всего мира ведут активную работу по поиску таких многочленов. Известен неприводимый многочлен степени x61 + x3 +1, а для n > 61 данных найти не удалось. Разложение многочленов на множители над конечными полями связанны с проблемами построения линейных рекуррентных последовательностей над конечными полями, которые в свою очередь лежат в основе построения современных криптосистем (рассмотрены далее).
Пусть F – произвольное поле и f(x) Î F[x]. Тогда замена переменной x в многочлене f(x) произвольным элементом b Î F обращает этот многочлен в корректно определенный элемент поля F. Если f(x) = a0+a1x +...+anxn Î F[x] и bÎ F, то, заменяя x на b, получаем элемент f(b) = a0 + a1b +...+ anbn Î F. Элемент f(b) называют значением многочлена f(x) при x = b. Если в кольце F[x] имеется какое-либо полиномиальное равенство, то заменяя в нем x на bÎ F, получаем равенство в поле F. (Принцип подстановки). Элемент b Î F называют корнем (или нулем) многочлена f(x) Î F[x], если при x = b f(b) = 0. Элемент b Î F является корнем многочлена f(x) Î F[x] тогда и только тогда, когда многочлен x - b делит f(x) (т.е. x - b|f(x)).
Существует связь между отсутствием корней и неприводимостью многочленов. Если f(x) – неприводимый многочлен из F[x] степени n ³ 2, то согласно теореме он не имеет корней в поле F. Обратное утверждение справедливо только для многочленов степени 2 и 3.
Теорема. Для неприводимости многочлена f(x) Î F[x] степени 2 и 3 в кольце F[x] необходимо и достаточно, чтобы он не имел корней в поле F.
Пример 29. Пользуясь этой теоремой, можно найти неприводимые многочлены степени 2 и 3 в кольце F2[x] над конечным полем F2. Исключаем из всей совокупности многочленов указанной степени, принадлежащих кольцу F2[x], те многочлены, которые имеют корни в поле F2. Тогда получим, что в кольце F2[x] имеется только один неприводимый многочлен степени 2: f(x) = x2 + x + 1 и два неприводимых многочлена степени 3: f(x) = x3 + x + 1, f(x) = x3 + x2 + 1.
Действительно: многочлены степени 2 – это f1= x2 + 1, f2 = x2 + x, f3 = x2 + x + 1.
Подставляя в них вместо x элементы поля F2, т.е. 0 или 1, видно, что f1 = 0 при x = 1, f2 = 0 при x = 1 и x=0, а f3 ¹ 0 при любом x Î { 0, 1}. Тоже самое и для многочленов степени 3: f1 = x3 + x2 + x +1, f2 = x3 + x2 +1, f3 = x3 + x +1, f4 = x3 + x2 + x, f5 = x3 + x 2 … ▲
3.4 Порядок многочлена
У каждого ненулевого многочлена f(x) над конечным полем кроме его степени deg(f(x)) имеется еще одна важная целочисленная характеристика – его порядок.
Если f (x) Î Fq [ x ] многочлен степени m ³ 1, удовлетворяющий условию f(0) ¹ 0, то существует натуральное число e ≤ qm - 1, для которого двучлен xe -1 делится на f(x).
Этот факт позволяет ввести определение порядка многочлена над конечным полем.
Определение. Пусть f (x) Î Fq [ x ] ненулевой многочлен. Если f (0) ¹ 0, то наименьшее натуральное число е, для которого многочлен f (x) делит (xe -1) называется порядком многочлена f (x) и обозначается ord (f (x)). Если же f(0) = 0, то многочлен f (x) однозначно представим в виде f (x) = xh·g (x) где h Î N, g (x) Î Fq [ x ] и g(0) = 0 и тогда ord (f (x)) многочлена f (x) определяется как ord (g (x)).
Порядок многочлена иногда называют его периодом или экспонентой многочлена. Порядок неприводимого многочлена можно определить, пользуясь следующей теоремой.
Теорема. Пусть f (x) Î Fq [ x ] неприводимый многочлен степени m, удовлетворяющий условию f(0) ¹ 0. Порядок этого многочлена совпадает с порядком любого корня этого многочлена в мультипликативной группе F* поля Fqm.
Отсюда вытекает важное следствие: Если f (x) Î Fq [ x ] неприводимый многочлен степени m над полем Fq, то его порядок ord (f (x)) делит число qm -1.
Значения порядков многочленов играют важную роль при формировании линейных рекуррентных псевдослучайных последовательностей над конечными полями и кольцами, которые в свою очередь являются основой для создания потоковых криптосистем.
|
|