Бинарные отношения 1 страница

Для любых двух множеств X и Y всякое подмножество R Ì X × Y называется бинарным отношением между X и Y (или просто на X, если X = Y).

Бинарное отношение R на множестве X называется:

1. Симметричным: если a R b, то b R a; (Если Иванов " учится в одной группе" с Петровым, то и обратное справедливо. Если прямая А " перпендикулярна" прямой B, то и обратное справедливо).

2. Антисимметричным: если a R b и b R a то а = b; (Если 1000 рублей можно разменять сотнями, то обратно не возможно).

3. Рефлексивным: если a R а; (это когда отношение обращено на себя. Ранее уже рассматривалось отношение включения. Поскольку любое множество включено само в себя, то отношение включения обладает свойством рефлексивности. Если верить народной мудрости, то и отношение " спасения" на множестве утопающих - рефлексивно).

4. Транзитивным, если a R b и b R c, то a R c (Если Иванов " учится в одной группе" с Петровым, а Петров с Сидоровым, то Иванов " учится в одной группе" с Сидоровым.

Симметричное, рефлексивное и транзитивное отношение R называется эквивалентностью.

Подмножество H = {x'Î X|x'~x}Î X всех элементов, эквивалентных данному x, называется классом эквивалентности, содержащим x.

Так как x~x (условие 1, симметричности), то x'Î H. Любой элемент x'Î H называется представителем класса H.

Справедлива следующая теорема. Множество классов эквивалентности по отношению ~ (R) является разбиением множества X в том смысле, что X является объединением непересекающихся подмножеств.

Отношение эквивалентности на множестве S разбивает это множество S на попарно непересекающиеся подмножества. Объединяя все элементы множества S, эквивалентные некоторому фиксированному элементу sÎ S, получим класс эквивалентности элемента s, который обозначается: [s] = {t Î S | (s, t) Î R}.

...

[n -1]={..., -n -1, -1, n -1, 2n -1, 3n -1,...}

Теорема. Бинарное отношение является эквивалентностью тогда и только тогда, когда оно разбивает множество, на попарно непересекающиеся классы.

Доказательство. Пусть отношение является эквивалентностью. Объединим все элементы, эквивалентные данному элементу a, в один класс К_а. Элементы в этом классе попарно эквивалентны в силу транзитивности: если a ~ b и a ~ c, то b ~ c. Кроме того, все элементы, эквивалентные какому – либо элементу класса, принадлежат этому же классу, что также следует из свойства транзитивности. Таким образом, каждый класс задается любым своим элементом: если a ~ b, то K_a = K_b. Если построить сначала класс элементов, эквивалентных a, а затем класс элементов, эквивалентных b, то эти два класса будут совпадать при a ~ b, и не будут пересекаться в противном случае.

2. МНОЖЕСТВА С АЛГЕБРАИЧЕСКИМИ ОПЕРАЦИЯМИ

2.1 Группы

Известны две операции на множестве Z целых чисел: сложение и умножение. Обобщим понятие операции на произвольное множество. Пусть S – некоторое множество и пусть S ´ S обозначает множество упорядоченных пар (s, t), где s Î S и t Î S. Бинарной алгебраической операцией (или законом композиции) на S называется произвольное (но фиксированное) отображение φ: S ´ S → S ( декартова квадрата S² = S ´ S в S). Таким образом, любой упорядоченной паре (s, t) элементов s, t∈ S ставится в соответствие определенный элемент φ (s, t) того же множества S.

Иногда вместо φ (s, t) пишут s φ t, а еще чаще бинарную операцию на множестве обозначают каким-нибудь специальным символом: *, ·, или +.

На множестве может быть задано, вообще говоря, много различных операций. Желая выделить одну из них, используют скобки (X, *) и говорят, что операция * определяет на X алгебраическую структуру или что (X, *) – алгебраическая система.

Бинарная операция · на множестве X называется ассоциативной, если (a · b) ·c = a · (b · c) всех a, b, c Î X. Она также называется коммутативной, если a · b = b · a. Те же названия присваиваются и соответствующей алгебраической структуре (X, ·). Требования ассоциативности и коммутативности независимы.

Представителем такой алгебраической структуры с одной операцией является группа.

Группой (G, *) (в дальнейшем группу будем обозначать просто G) называется некоторое множество G c бинарной операцией * на нем, для которого выполняются следующие условия:

1. Операция * ассоциативна, т.е. для любых а, b, c Î G справедливо

a *(b *c) = (a * b) * с.

2. В G существует единичный элемент (или единица) е такой, что для любого аÎ Gа * е = e * a = a

3. Для каждого аÎ G существует обратный элемент a^-1 Î G, такой что

a * a^-1 = a^-1 * a = e

Если группа G удовлетворяет также следующему условию: для любых а, b Î G справедливо а * b = b * а, то она называется коммутативной или абелевой группой.

Единичный e и обратный а^-1 элемент группы G для каждого данного элемента а Î G определяется однозначно указанными выше условиями. Для всех элементов а, b Î G имеет место равенство (a * b)^-1 = b^-1 * a^-1. Для групповой операции * может быть использовано мультипликативное обозначение, как для обычного умножения. Тогда вместо а * b можно просто записать а ´ b или аb. Однако при этом не предполагается, что операция * – это простое умножение. В ряде случаев для групповой операции * может быть использована аддитивная запись а + b вместо а * b. Тогда элемент группы G а + b называют суммой элементов а, b. Применяют 0 вместо е (единичный элемент в мультипликативной записи) и -а вместо a^-1. Такие обозначения обычно используются для абелевых групп.

Если а Î G и nÎ N в мультипликативной записи пишут aⁿ = a · a·... · a (n сомножителей a)и элемент aⁿ называют n - йстепенью числа а.

Если для групповой операции используется +т.е. аддитивное обозначение, то вместо aⁿ будем иметь nа = а + а +... + а (n слагаемых а).

Для n = 0 Î Z имеем a⁰ = e в мультипликативных обозначениях и 0 ·а = 0 в аддитивных обозначениях.

Множество, состоящее из единственного элемента е с операцией *, определенной условием е*е = е, является группой.

Группа, образованная положительными и отрицательными степенями одного элемента a называется циклическо й. Это обозначает, что мультипликативная группа G является циклической, если она порождена одним элементом, то есть в ней имеется такой элемент а (называется образующим), что любой другой элемент b представим в виде b = aⁿ , n Î Z. Для циклической группы G применяют обозначения G = < a>.

< a> = {..., a^-n,... a^-1, a⁰ = e, a,..., aⁿ,...}.

Из определения следует, что циклическая группа является коммутативной или абелевой. Если в циклической группе нет одинаковых элементов, то она называется свободной.

Циклическая группа является конечной, если среди её элементов есть равные. Если a^k = a^m при k > m, то a^k-m = e, так что в этом случае некоторая степень с натуральным показателем образующей группы равна e. Наименьший натуральный показатель, обладающий этим свойством, называется порядкомэлемента a. Если порядок элемента a равен n, то среди элементов e, a,..., a^n-1 нет равных.

Для любого элемента b циклической группы порядка n имеет место равенство bⁿ = e. Если порядок циклической группы < a> является простым, то < a> не имеет подгрупп, отличных от {e} и < a>, в противном случае циклическая группа имеет подгруппы.

Если a – образующий элемент конечной циклической группы G порядка n, то каждому элементу b Î G можно взаимно однозначно сопоставить его (скалярный) индекс или дискретный логарифм – целое число m, 0 ≤ m ≤ n-1, такое, что b = a^m.

Пусть a – некоторый элемент группы G. Тогда элементами группы G будут также ..., a^-2, a^-1, a⁰ = e, a, a², a³,.... Если G содержит ещё один элемент b, не являющийся степенью элемента a, то элементами группы G являются и всевозможные произведения ab, ba, a^-1bba, baab^-1ab и вообще произвольные конечные произведения вида aⁿ¹ bⁿ² aⁿ³ bⁿ⁴..., где n_i Î Z. Среди этих произведений могут быть равные. Такие произведения образуют подгруппу H группы G. Если группа H бесконечна, то она называется свободной группой, образованной элементами a и b, а сами элементы a и b называются образующими группы H. В циклической группе, конечной или нет, может быть несколько образующих элементов и ни один из них не представим в виде произведения других элементов.

Пример 8. В аддитивной циклической группе Z образующими будут элементы 1 и –1. Образующими группы Q рациональных чисел по умножению являются все простые числа. ▲

Множество образующих можно рассматривать как множество букв из некоторого алфавита S, при этом если a – буква, a^-1 – тоже буква. Из букв можно составлять слова, в том числе однобуквенные и пустое слово, не содержащее ни одной буквы. В словах допускаются сокращение, при котором подряд стоящие буквы aa^-1 или a^-1a вычеркиваются. Определим операцию умножения слов как конкатенацию, то есть приписывание к первому слову второго слова. Символ конкатенации не представлен ни одной буквой. Например (abbc) ∙ (c^-1bca) = abbbca. Эквивалентность слов определим как их совпадение с учетом указанного сокращения. Такое умножение определено на всех словах и обладает ассоциативностью. Единичным элементом является пустое слово; каждое слово имеет обратное, записанное " задом наперёд" и состоящее из обратных букв. Например, обратным к слову abca^-1c будет слово c^-1ac^-1b^-1a^-1.

Группа, образованная множеством { [0], [1],..., [n -1]} классов вычетов по модулю n с операцией [a]+[b] = [a+b], называется группой классов вычетов по модулю n и обозначается Z_n. Группа Z_n является циклической с образующим элементом [1] и имеет порядок n.

Группа называется конечной (бесконечной), если она состоит из конечного (бесконечного) числа элементов. Число элементов конечной группы G называется ее порядком и обозначается | G |, Card G и (G: e).

Каждая группа содержит некоторые подмножества, которые сами образуют группу с той же групповой операцией.

Подмножество Н группы G называется подгруппой этой группы, если Н образует группу относительно операций группы G.

Свойства циклических групп:

1.Каждая подгруппа циклической группы также является циклической.

2.В конечной циклической группе < a> порядка m элемент a^k порождает подгруппу порядка m ⁄ НОД(k, m).

3.Для любого положительного делителя q порядка m циклическая группа < a> содержит в точности одну подгруппу порядка q.

4.Пусть q положительный делитель порядка конечной циклической группы < a>. Тогда < a> содержит φ (q) элементов порядка q. (Напомним, что φ (q) – функция Эйлера: число целых чисел k 1 ≤ k ≤ q, взаимно простых с числом q).

5.Конечная циклическая группа < a> порядка m содержит φ (m) образующих (т.е. таких элементов a^r, что < a ^r> = < a>). Образующими являются те и только те степени a^r элемента а, для которых (r, m) = 1 (т.е. r и m взаимно простые числа).

2.2. Группы подстановок

Подстановка – это взаимно однозначное (биективное) отображение конечного множества в себя. При соответствующей нумерации (упорядочении) элементов конечного множества, на котором определена подстановка, её можно свести к подстановке на некотором конечном подмножестве натуральных чисел. Любая подстановка является элементом некоторой группы, задающей взаимно однозначное отображение этого множества в себя.

Пусть σ – конечное множество из n элементов. Поскольку природа этих элементов для нас несущественна, удобно считать, что σ ={1, 2, …, n}. Группа S(σ) всех взаимно однозначных отображений σ → σ называется симметрической группой степени n (или: симметрической группой на n символах или на n точках) и чаще обозначается через S_n. Ее элементы, обычно обозначаемые строчными буквами греческого алфавита, являются подстановками (или перестановками).

Подстановки можно представлять различным образом: в виде таблицы, в виде функции, в виде произведения циклов.

В наглядной форме перестановку σ: i→ σ (i), i = 1, 2, …, n, изображают двухрядным символом:

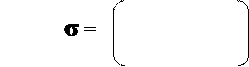1 2 3... n

i₁ i₂ i₃... i_n

полностью указывая все образы:

N

σ: ↓ ↓ ↓ ↓

i₁ i₂ i₃... i_n

где i_k = σ (k), k = 1, 2, …, n, – переставленные символы 1, 2, …, n. Как всегда, e – единичная перестановка e(i) = i для любых i. Ее обычно не показывают.

Более коротко перестановки записываются в виде σ = (i₁, i₂,..., i_n).

Пример 9. Обычно подстановка представляется в виде таблицы из двух строк: первая содержит числа 1, 2,..., n в естественном порядке, а вторая – образы соответствующих элементов первой строки. Примем для n = 9

▲

Рассмотрим результаты многократного применения подстановки к множеству чисел, на котором она определена. Поскольку это множество конечно, то для числа а и подстановки S последовательность а, S(а), S(S(а)) = S²(а), S³(а), ... даёт цикл, образованный элементом а. Такой же цикл дают любые числа, лежащие в цикле, образованным числом а. Выбрав число b, не принадлежащее этому циклу, можно построить другой цикл, образованный числом b. Продолжая эту процедуру до тех пор, пока не будут перечислены все числа 1, 2,..., n, получим представление подстановки в виде совокупности непересекающихся циклов. В примере 9 имеются следующие циклы: (6), (1, 5, 7), (2, 3, 8, 4, 9). Длины циклов, образованных числами 6, 1, 2, равны, соответственно 1, 3, 5.

Подстановка вида i₁ → i₂ → i₃ → ··· → i_k → i₁ называется циклом длиной k и обозначается (1, 2,..., k). Два цикла называются независимыми, если перемещаемые ими элементы попарно различны. Независимые циклы коммутируют, то есть для них выполняется условие: σ ₁ σ ₂ = σ ₂ σ ₁. Цикл длиной k =2 называется транспозицией. Каждая подстановка единственным образом разложима в произведение независимых циклов и каждая подстановка является произведением транспозиций.

Если в общем случае подстановка разбивается на циклы длины k₁, k₂,... k_r, то подстановка, полученная возведением исходной подстановки в степень, равную произведению длин циклов k _j, дает тождественную подстановку.

Пример 10. Примем:

4 6 1 5 3 2 6 5 4 3 2 1

Тогда произведение подстановок (композиция подстановок) определяется как последовательное выполнение этих подстановок.

1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6

6 5 4 3 2 1 4 6 1 5 3 2 2 3 5 1 6 4

(σ (1→ 6) (φ (6→ 2) → (σ φ (1→ 2)

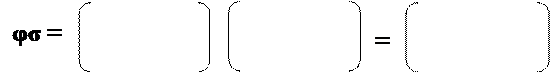В то же время

1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6

4 6 1 5 3 2 6 5 4 3 2 1 3 1 6 2 4 5

т.е. σ φ ≠ φ σ. ▲

Мощность группы (число её элементов) равно |S| = n!.

Разложим теперь перестановки из S_n в произведения более простых перестановок. Идея разложения поясняется на перестановках из примера 10. Перестановку σ можно записать разными способами:

1 2 3 4 5 6 1 4 5 3 2 6

4 6 1 5 3 2 4 5 3 1 6 2

Нетрудно заметить, что по существу σ оказалась разложенной на две части:

1 4 5 3 и 2 6

4 5 3 1 6 2

Первые четыре места содержат сведения, как σ воздействует на числа 1, 3, 4 и 5, а вторые два места хранят информацию о воздействии σ на цифры 2 и 6.

Более коротко это записывается так: σ =(1 4 5 3)(2 6); φ =(1 6)(2 5)(3 4); σ φ =(1 2 3 5 6 4); α = φ σ = (1 3 6 5 4 2).

Перестановка α =(1 3 6 5 4 2) = (3 6 5 4 2 1) = (6 5 4 2 1 3) = (5 4 2 1 3 6) = (4 2 1 3 6 5) = (2 1 3 6 5 4) носит название цикла длины 6, а перестановка σ =(1 4 5 3)(2 6) – есть произведение двух независимых (непересекающихся) циклов длины 4 и 2.

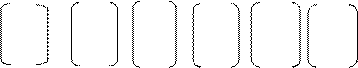Пример 11. Группа S₃ состоит из 6 подстановок.

1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3

1 2 3, 1 3 2, 2 1 3, 2 3 1, 3 1 2, 3 2 1 ▲

Свойства подстановок:

1. Каждая подстановка единственным образом разложима в произведение независимых циклов.

2. Каждая подстановка является произведением транспозиций.

2.3. Морфизмы групп

2.3.1. Изоморфизмы

Две группы G и G' с операциями * и ○ называются изоморфными, если

существует отображение f: G→ G' такое, что:

1. f(a*b) = f(a)○ f(b) для всех a, b Î G;

2. f – биективно.

Факт изоморфизма групп обозначается символически @.

Отметим простейшие свойства изоморфизма.

1. Единица переходит в единицу. Действительно, если e – единица группы

G, то e*a = a*e = a, и значит f(e)○ f(a) = f(a)○ f(e) = f(a), откуда следует, что f(e) = e' – единица группы G'. В этом рассуждении использованы, хотя и частично, оба свойства f. Для (1) это очевидно, а свойство (2) обеспечивает сюръективность f, так что элементами f(g) исчерпывается вся группа G'.

2. f(a^-1) = f(a)^-1. В самом деле, согласно ( 1 ), f(a)○ f(a^-1) = f(a*a^-1) = f(e) = = e' – единица группы G', откуда f(a)^-1 = f(a)^-1○ e' = f(a)^-1○ (f(a)○ f(a^-1)) = (f(a)^-1○ f(a))○ f(a^-1) = e'○ f(a^-1) = f(a^-1).

3. Обратное отображение f^-1: G→ G' (существующее в силу свойства 2)

тоже является изоморфизмом. Для этого надо убедиться лишь в справедливости свойства (1) для f^-1. Пусть a', b'Î G'. Тогда ввиду биективности f имеем a' = f(a), b'= f(b) для каких-то a, b Î G. Поскольку f – изоморфизм, a'○ b'= f(a)○ f(b) = f(a*b). Отсюда имеем a*b = f^-1(a'○ b'), а так как, в свою очередь, a = f^-1(a'), b = f^-1(b'), то f^-1(a'○ b') = f^-1(a') * f^-1(b').

Рассмотрим теперь теорему, иллюстрирующую роль изоморфизма в теории групп.

Теорема Кэли. Любая конечная группа порядка n изоморфна некоторой подгруппе симметрической группы S_n (без доказательства).

Теорема Кэли, несмотря на свою простоту, имеет важное значение в теории групп. Она выделяет некий универсальный объект (семейство {S_n|n=1, 2, …} симметрических групп) – вместилище всех вообще конечных групп, рассматриваемых с точностью до изоморфизма. Фраза " с точностью до изоморфизма" отражает сущность не только теории групп, стремящейся объединить в один класс все изоморфные группы, но математики в целом, которая без таких обобщений была бы лишена смысла.