Математические основы криптологии

Учебное пособие

Предлагаемое издание рекомендуется в качестве учебного пособия по дисциплине " Математические основы криптологии" для студентов специальности 075400. В учебном пособии изложены базовые материалы математических основ криптографической защиты информации. Цель курса – снабдить студентов математическим аппаратом, необходимым для описания математических моделей шифров и расчета их криптографических характеристик. В основе курса лежит подход к математической модели шифра как полиномиальной функции универсальной алгебры. Более подробно изучаются классические алгебраические структуры (конечные кольца и поля). Рассматриваются принципы построения симметричных и асимметричных криптосистем, блочных и потоковых шифров. В качестве криптографических приложений изучается теория линейных рекуррентных последовательностей над конечным полем, смешанный конгруэнтный метод построения псевдослучайных последовательностей.

СОДЕРЖАНИЕ

Введение............................................................................................................5

1. Множества и отображения.......................................................................13

1.2. Операции над множествами.....................................................................15

1.3. Отображения множеств............................................................................19

1.4. Бинарные отношения................................................................................22

2. Множества с алгебраическими операциями...........................................25

2.1. Группы........................................................................................................25

2.2. Группы перестановок................................................................................30

2.3. Морфизмы групп.......................................................................................33

2.4. Коммутативные кольца.............................................................................36

2.5. Гомоморфизмы и идеалы колец...............................................................38

2.6. Типы колец.................................................................................................41

2.7. Поле.............................................................................................................43

3. Кольцо многочленов..................................................................................48

3.1. Основные понятия и определения............................................................48

3.2. Разложение в кольце многочленов...........................................................50

3.3. Неприводимые многочлены......................................................................52

3.4. Порядок многочлена..................................................................................54

4. Теоретико – числовые модели криптологии............................................58

4.1. Основная теорема арифметики..................................................................58

4.2. Свойства чисел............................................................................................58

4.3. Алгоритм деления с остатком в множестве целых чисел.......................59

4.4. Алгоритм Евклида......................................................................................60

4.5. Диафантово уравнение первой степени...................................................61

4.6. Функция Эйлера.........................................................................................67

4.7. Решение сравнений первой степени.........................................................67

4.8. Система сравнений первой степени..........................................................69

4.9. Вычисление сравнений вида a^b(mod m)....................................................72

5. Основные понятия и определения в криптографии.................................74

5.1. Понятие шифра...........................................................................................74

5.2. Симметричные криптоалгоритмы............................................................79

6. Асимметричные криптосистемы..............................................................94

6.1. Односторонние функции...........................................................................94

6.2. Генерация ключей......................................................................................97

6.3. Асимметричная криптосистема RSA.....................................................101

6.4. Надежность системы RSA.......................................................................106

6.5. Проблемы практической реализации RSA............................................109

6.6. Алгоритм Эль – Гамаля...........................................................................111

6.7. Криптосистемы на базе эллиптических кривых...................................113

7. Аутентификация и электронная цифровая подпись..............................118

7.1. Протоколы аутентификации...................................................................118

7.2. Алгоритмы использования электронной цифровой подписи..............123

8. Элементы теории равномерно распределенных случайных

последовательностей.................................................................................129

8.1. Линейные регистры сдвига с обратной связью.....................................130

8.2. Линейные рекуррентные последовательности......................................132

8.3. Линейные и мультипликативные конгруэнтные генераторы...............137

8.4. Нелинейные конгруэнтные генераторы..................................................139

8.5. Криптографические генераторы на основе односторонней функции..140

Список рекомендованной литературы.....................................................142

ВВЕДЕНИЕ

Криптология (от греческого kryptos - тайный и logos - сообщение), – наука о создании и анализе систем безопасной передачи и хранения информации. Криптологию условно подразделяют на два направления. Первое направление называется криптографией, второе – криптоанализом.

Предметом криптографии является разработка и использование методов и средств, предназначенных для защиты процессов информационного взаимодействия между легальными сторонами, от целенаправленных воздействий со стороны злонамеренных субъектов, называемых злоумышленниками.

Криптоанализ – раздел криптологии, разрабатывающий методы анализа криптографических систем, раскрытия зашифрованных данных, а также способы подделки и подмены защищаемой информации.

Если криптологию трактовать в более широком смысле, то необходимо включить ещё один раздел – стеганографию (если буквально переводить с греческого – тайнопись) – направление развития криптологии, разрабатывающее методы скрытия сообщений в потоке передаваемой информации.

Впервые термин " криптография", обозначающий " секретное письмо" введен в 1641 году англичанином Дж. Уилкинсом, который имел в виду " открытое секретное письмо" в том смысле, что зашифрованность письма не скрывалась. Термин " стеганография" введен в 1665 году К. Шоттом, при этом имелось в виду " скрытое секретное письмо", в том смысле, что тайной является сам факт передачи секретного сообщения.

В настоящее время существует большое разнообразие видов защищаемой информации: документальная, телеметрическая, телефонная, компьютерная и т.д. и т.п. Каждый вид информации имеет свои специфические особенности, и эти особенности сильно влияют на выбор методов шифрования информации. Большое значение имеют объемы и скорость передачи шифрованной информации.

Выбор вида шифра и его параметров существенно зависит от характера защищаемых секретов. Некоторые тайны (например, государственные, военные и др.) должны сохраняться десятилетиями, а некоторые (например, биржевые) – уже через несколько часов можно разгласить. Необходимо учитывать возможности противника, от которого защищается данная информация. Одно дело – противостоять одиночке или группе преступников, а другое дело – мощной государственной структуре.

Для профессионального понимания криптографических алгоритмов и умения оценивать их сильные и слабые стороны, необходима соответствующая математическая подготовка. Это объясняется тем, что современная криптография основана на глубоких результатах таких разделов математики, как теория сложности вычислений, теория чисел, алгебра и т.д.

Долгое время криптография как один из разделов науки была засекречена, т.к. применялась, в основном, для защиты государственных и военных секретов. Термин " криптология" даже нельзя было произносить тем, кто профессионально работал в этой области, не говоря уже о каких бы то ни было открытых публикациях на эту тему. Слово " криптология" впервые появилось у нас в переводной статье Дж. Л. Месси " Введение в современную криптологию" в тематическом выпуске журнала ТИИЭР, т.76, № 5 за 1988 год. Начало открытой теоретической криптографии положила статья Клода Шеннона " Теория связи в секретных системах", опубликованная в 1949 году (эта статья была написана в 1945 году и была сразу засекречена).

В настоящее время, методы и средства криптографии используются для обеспечения информационной безопасности не только государства, но и частных лиц и организаций. Дело здесь совсем не обязательно в секретах, а в том, что сейчас очень большой обмен информацией происходит в цифровом виде через открытые каналы связи. К этой информации возможно применение угроз несанкционированного ознакомления, подмены, фальсификации и т.д. Наиболее надежные методы защиты от таких угроз дает именно криптография.

Интеграция России в международное сообщество ведет к росту числа используемых зарубежных криптографических систем. Специалисты по защите информационных ресурсов должны знать особенности работы алгоритмов, наличие уязвимостей, уровень криптостойкости и т. д.

Быстрое развитие криптографии приводит к расширению её предметной области и росту числа методов исследования. Принято различать традиционную криптографию с секретным ключом (также используют названия симметричные или одноключевые криптоалгоритмы) и современную криптографию с открытым ключом (двухключевые или асимметричные алгоритмы). Это разделение обусловлено не тем, что ключ является секретным или открытым, а типом математической задачи, положенной в основу соответствующих криптоалгоритмов, и, следовательно, методами решения этой задачи.

Математическая криптография возникла как наука о шифровании информации, т.е. как наука о криптосистемах. В классической модели системы секретной связи (описанной Клодом Шенноном) имеют место два полностью доверяющих друг – другу участника, которым необходимо передавать между собой информацию, не предназначенную для третьих лиц. Такая информация называется конфиденциальной или секретной. Отсюда возникает задача обеспечения конфиденциальности, т.е. защита секретной информации от противника. Эта задача, по крайней мере, исторически – первая задача криптографии. Она традиционно решается с помощью шифрования данных.

В настоящее время криптографические криптоалгоритмы используются во многих направлениях по защите информации. Так при обмене информацией между участниками часто возникает ситуация, когда информация не является конфиденциальной, но важен факт поступления сообщений в неискаженном виде, т.е. обеспечение гарантии, что никто не сумеет подделать сообщение. Такая гарантия называется обеспечением целостности информации и составляет вторую задачу криптографии, в которой используются алгоритмы электронной цифровой подписи.

Для предотвращения угрозы контроля за источниками информации (откуда пересылаются сообщения) необходима система контроля за доступом к ресурсам, которая должна удовлетворять двум, казалось бы, взаимно исключающим требованиям. Во – первых, всякий желающий должен иметь возможность обратиться к этой системе анонимно, а во – вторых, доказать свое право на доступ к ресурсам. Примером могут служить бумажные купюры. Если ресурсом является некоторый товар, то наличие у покупателя достаточного количества купюр является доказательством его права на доступ к ресурсу. С другой стороны, хотя каждая бумажная купюра и имеет уникальный номер, отслеживать купюры по номерам практически невозможно, т.е. нельзя определить, кто ее использовал и в каких платежах. Аналог этого свойства в криптографии называется неотслеживаемостью. Обеспечение неотслеживаемости – третья задача криптографии.

Задача обеспечения конфиденциальности решается с помощью криптосистем, а для обеспечения целостности и неотслеживаемости разрабатываются специальные криптографические протоколы.

Примеры из истории криптографии

Потребность шифровать и передавать шифрованные сообщения возникла очень давно. Так, еще в V-IV вв. до н. э. греки применяли специальное шифрующее устройство. По описанию Плутарха, оно состояло из двух палок одинаковой длины и толщины. Одну оставляли себе, а другую отдавали отъезжающему. Эти палки называли скиталами. Когда правителям нужно было сообщить какую-нибудь важную тайну, они вырезали длинную и узкую, вроде ремня, полосу папируса, наматывали ее на свою скиталу, не оставляя на ней никакого промежутка, так чтобы вся поверхность палки была охвачена этой полосой. Затем, оставляя папирус на скитале в том виде, как он есть, писали на нем все, что нужно, а написав, снимали полосу и без палки отправляли адресату. Так как буквы на ней разбросаны в беспорядке, то прочитать написанное можно только при помощи соответствующей скиталы, намотав на нее без пропусков полосу папируса.

Аристотелю принадлежит способ дешифрования этого шифра. Надо изготовить длинный конус и, начиная с основания, обертывать его лентой с шифрованным сообщением, постепенно сдвигая ее к вершине. В какой - то момент начнут просматриваться куски сообщения. Так можно определить диаметр скиталы.

Были и другие способы защиты информации, разработанные в античные времена. Например, древнегреческий полководец Эней Тактика в IV веке до н.э. предложил устройство, названное впоследствии " диском Энея". Принцип его таков. На диске диаметром 10-15 см и толщиной 1-2 см высверливались отверстия по числу букв алфавита. В центре диска помещалась " катушка" с намотанной на ней ниткой достаточной длины. При зашифровании нитка " вытягивалась" с катушки и последовательно протягивалась через отверстия, в соответствии с буквами шифруемого текста. Диск и являлся посланием. Получатель послания последовательно вытягивал нитку из отверстий, что позволяло ему получать передаваемое сообщение, но в обратном порядке следования букв. При перехвате диска противник имел возможность прочитать сообщение тем же образом, что и получатель. Но Эней предусмотрел возможность легкого уничтожения передаваемого сообщения при угрозе захвата диска. Для этого было достаточно выдернуть " катушку" с закрепленным на ней концом нити до полного выхода всей нити из всех отверстий диска.

Сам термин " шифр" арабского происхождения. В начале XV в. арабы опубликовали энциклопедию “Шауба Аль-Аша”, в которой есть специальный раздел о шифрах. В этой энциклопедии указан способ раскрытия шифра простой замены. Он основан на различной частоте повторяемости букв в тексте. В этом разделе есть перечень букв в порядке их повторяемости на основе изучения текста Корана. Заметим, что в русском тексте чаще всего встречается буква " О", затем буква " Е" и на третьем месте стоят буквы " И" и " А".

В Древней Греции идея Энея была использована при создании и других оригинальных шифров замены. Например, в одном из вариантов вместо диска использовалась линейка с числом отверстий, равных количеству букв алфавита. Каждое отверстие обозначалось своей буквой; буквы по отверстиям располагались в произвольном порядке. К линейке была прикреплена катушка с намотанной на нее ниткой. Рядом с катушкой имелась прорезь. При шифровании нить протягивалась через прорезь, а затем через отверстие, соответствующее первой букве шифруемого текста, при этом на нити завязывался узелок в месте прохождения ее через отверстие; затем нить возвращалась в прорезь и аналогично зашифровывалась вторая буква текста и т.д. После окончания шифрования нить извлекалась и передавалась получателю сообщения. Тот, имея идентичную линейку, протягивал нить через прорезь до отверстий, определяемых узлами, и восстанавливал исходный текст по буквам отверстий.

Это устройство получило название " линейка Энея". Шифр, реализуемый линейкой Энея, является одним из примеров шифра замены: буквы заменяют на расстояния между узелками с учетом прохождения через прорезь. Ключом шифра являлся порядок расположения букв по отверстиям в линейке. Противник, завладевший нитью (даже имея линейку, но без нанесенных на ней букв), не сможет прочитать сообщение.

Заметным вкладом Энея в криптографию является предложенный им так называемый книжный шифр, описанный в сочинении " Об обороне укрепленных мест". Эней предложил прокалывать малозаметные дырки в книге или в другом документе над буквами (или под ними) секретного сообщения. Интересно отметить, что в первой мировой войне германские шпионы использовали аналогичный шифр, заменив дырки на точки, наносимые симпатическими чернилами на буквы газетного текста. Книжный шифр в современном его виде имеет несколько иной вид. Суть этого шифра состоит в замене букв на номер строки и номер этой буквы в строке и заранее оговоренной странице некоторой книги. Ключом такого шифра является книга и используемая страница в ней. Этот шифр оказался " долгожителем" и применялся даже во времена второй мировой войны.

В Древней Греции (II в. до н. э.) был также известен шифр, называемый квадрат Полибия. Это устройство представляло собой квадрат 5 ´ 5, столбцы и строки которого нумеровали цифрами от 1 до 5. В каждую клетку этого квадрата записывалась одна буква. (В греческом варианте одна клетка оставалась пустой, в латинском – в одну клетку помещали две буквы i и j.) В результате каждой букве отвечала пара чисел, и шифрованное сообщение превращалось в последовательность пар чисел.

Пример. 13 34 22 24 44 34 15 42 22 34 43 45 32

Это сообщение записано при использовании латинского варианта квадрата Полибия, в котором буквы расположены в алфавитном порядке. (" Cogito, ergo sum" – лат, " Я мыслю, следовательно существую").

В несколько измененном виде шифр Полибия дошел до наших дней и получил своеобразное название " тюремный шифр". Для его использования нужно только знать естественный порядок расположения букв алфавита (как в указанном выше примере для английского языка). Стороны квадрата обозначаются не буквами (ABCDE), а числами (12345). Число 3, например, передается путем тройного стука. При передаче буквы сначала отстукивается число, соответствующее строке, в которой находится буква, а затем номер соответствующего столбца. Например, буква " F" передается двойным стуком (вторая строка) и затем одинарным (первый столбец). С применением этого шифра связаны некоторые исторические казусы. Так, декабристы, посаженные в тюрьму после неудавшегося восстания, не смогли установить связь с находившимся в " одиночке" князем Одоевским. Оказалось, что этот князь (хорошо образованный по тем временам) не помнил естественный порядок расположения букв в русском и французском алфавитах (другими языками он не владел). Декабристы для русского алфавита использовали прямоугольник размера 5 ´ 6 (5 строк и 6 столбцов) и редуцированный до 30 букв алфавит.

В настоящее время широко известна история с немецкой шифровальной машинкой " Энигма", использовавшаяся во 2 – й мировой войне. Англичане, совместно с эмигрировавшими к ним польскими криптографами, сумели создать специализированную электронную машину, вскрывавшую ключи " Энигмы", и регулярно читали информацию противника (опубликовано несколько художественных и документальных книг, снят кинофильм). Однако мало кто знает, что и наши криптоаналитики сумели в 1943 году (к началу Курской битвы) тоже вскрыть немецкие шифры " Энигмы" и получать секретную информацию (публикации в журнале " Конфидент"). В этом же журнале была описана роль советских криптоаналитиков во время Карибского кризиса. Добытая ими информация о намерениях США послужила основанием для принятия решения Советским руководством о демонтаже ракет на Кубе и возвращении их в Советский Союз и, как следствие, преодоление Карибского кризиса, едва не приведшего к третьей мировой войне и ядерной катастрофе. Но Н.С. Хрущёв (в то время лидер СССР) публично прихвастнул своей информированностью, в результате чего американцы экстренно сменили свою шифротехнику.

1. МНОЖЕСТВА И ОТОБРАЖЕНИЯ

1.1 Множества

Множество – совокупность объединенных по некоторым признакам различных объектов, называемых элементами множеств.

Если а – элемент множества А, то говорят что а принадлежит А и обозначают а Î А. В противном случае – используют следующее обозначение а Ï А. Элементами множества могут быть другие множества, однако говорить о множестве всех множеств нельзя. Множество, состоящее из элементов a_i обозначается {a_i} или {a₁, a₂,..., a_i}.

Равные множества состоят из одних и тех же элементов.

Пустое множество - Æ не содержит ни одного элемента, по определению входит в число подмножеств любого множества.

Если каждый элемент множества А является элементом множества В, то А называется подмножеством множества В и обозначается А Í В. Если при этом А ≠ В, то говорят, что А является собственным подмножеством множества В, обозначается А Ì В. Если А Í В и А Ê В, то А = В.

По определению любое множество является собственным подмножеством или любое множество включено само в себя. А если два множества являются подмножествами друг друга, то они состоят из одних и тех же элементов.

Множество всех подмножеств данного множества А обозначается Р(А). Если A = {a, b, c}, P(A) ={{Æ }, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}.

Для некоторых особо важных множеств приняты стандартные обозначения, которых следует придерживаться.

N – множество натуральных чисел (1, 2, 3,...);

Z – множество целых чисел (0, ± 1, ± 2, ± 3,....);

Q – множество рациональных чисел: числа вида p/q, где p и q - целые числа и q ≠ 0. Класс рациональных чисел включает в себя все целые числа Z, которые в свою очередь включают в себя все натуральные числа N;

R - множество вещественных чисел: этот класс включает все рациональные числа и все числа не являющиеся таковыми т.е. все иррациональные числа.

Пример 1. Множеством может быть множество деревьев в лесу, множество студентов в университете и т.п. В данном примере множество состоит из элементов – деревьев, студентов. При этом никакой роли не играет, рассматриваем ли мы тех же студентов в порядке алфавита или по успеваемости. Недопустимы только двойники или студенты, у которых отсутствуют отличительные свойства. Естественно существуют множества, состоящие из чисел, в криптологии множествами могут быть:

· множество алфавитов;

· множества открытых текстов;

· множество криптограмм (шифротекстов);

· ключевые множества. ▲

Пример 2. Использование методов криптографической защиты информации можно определить как отображение некоторого множества возможных сообщений в другое пространство – множество возможных криптограмм. Каждое конкретное отображение из этого множества соответствует шифрованию при помощи конкретного ключа.

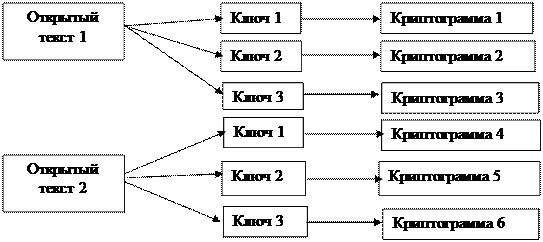Рисунок 1.1. Отображение множества открытых текстов в множество зашифрованных текстов ▲

Пример 3. Можно сказать, что множество студентов группы 941 включено в множество студентов университета МАИ, поскольку такая группа в университете числится. То, что из группы отчислены все студенты, для математики никакой роли не играет. Поскольку, нет ни одного студента, числящегося в этой группе, который бы не числился в университете.

Например, студент Сидоров не может быть подмножеством студентов университета, поскольку он сам не множество, а элемент. Поэтому он, как элемент, может быть лишь элементом множества студентов университета. А вот группа 941, как множество студентов, есть полноправное подмножество множества студентов университета. Но группа 941 состоит всего лишь из одного не отчисленного студента. Того самого Сидорова! Вот и получается, что сам Сидоров не может быть подмножеством, но группа, состоящая из него одного, может.

С другой стороны, если вдруг ректор решит рассматривать университет, как множество студенческих групп, то группа 941 станет элементом множества студенческих групп университета. Тут ничего страшного, если понимать, что множество студентов университета и множество студенческих групп университета – два разных множества. ▲