Математическое ожидание случайной величины, мода, медиана

Закон распределения полностью характеризует случайную величину. Однако часто закон распределения не известен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.

Математическое ожидание, как будет показано далее, приблизительно равно среднему значению случайной величины. Для решения многих задач достаточно знать математическое ожидание. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго. Хотя математическое ожидание дает о случайной величине значительно меньше сведений, чем закон ее распределения, но для решения задач, подобных приведенной и многих других, знание математического ожидания оказывается достаточным.

Математическое ожидание дискретной случайной величины Х, принимающей конечное множество значений с законом распределения

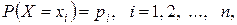
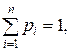
называется суммой произведений её значений на их соответствующие вероятности:

.

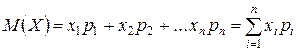Математическое ожидание дискретной случайной величины приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому всех ее возможных значений.

Пример 1.1. Найти математическое ожидание случайной величины Х, зная закон ее распределения

Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности

.

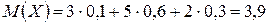Пример 1.2. Подбрасывается игральный кубик. Найти математическое ожидание дискретной случайной величины Х, равной числу выпавших очков.

Эта случайная величина может принимать шесть значений 1, 2, 3, 4, 5, 6. Вероятность каждого из них одна и та же, равная 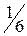. Закон распределения случайной величины Х можно задать формулой:

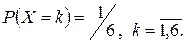
Тогда математическое ожидание равно

.

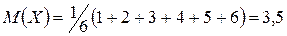Очевидно, что математическое ожидание больше наименьшего и меньше наибольшего возможных значений. Другими словами, на числовой оси возможные значения расположены слева и справа от математического ожидания. В этом смысле математическое ожидание характеризует расположение распределения и поэтому его часто называют центром распределения. Этот термин заимствован из механики: если массы р ₁, р ₂, …, р_п расположены в точках с абсциссами х ₁, х ₂, …, х_п, причем 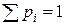, то абсцисса центра тяжести

.

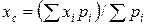Учитывая, что 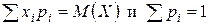, получим .

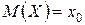Итак, математическое ожидание есть абсцисса центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы – их вероятностям.

Математическое ожидание дискретной случайной величины, принимающей бесконечную последовательность значений с законом распределения

,

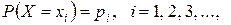
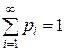определяется формулой , если этот ряд сходится абсолютно.

Математическое ожидание непрерывной случайной величины Х, все значения которой принадлежат отрезку 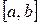, а 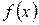– ее плотность вероятностей, определяется формулой

.

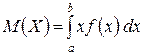Если все значения непрерывной случайной величины Х принадлежат бесконечному промежутку 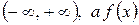– её плотность вероятностей, то математическое ожидание определяется формулой

,

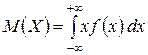когда этот несобственный интеграл сходится абсолютно, т. е. существует интеграл .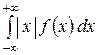

Очевидно, что математическое ожидание случайной величины есть неслучайная (постоянная) величина.

Пример 1.3. Плотность распределения вероятностей случайной величины Х задана функцией

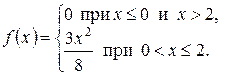
Найти математическое ожидание случайной величины Х.

.

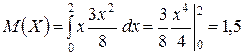Свойства математического ожидания случайных величин:

1. Значение математического ожидания случайной величины Х заключено между ее наименьшим и наибольшим значениями:

,

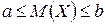где а – наименьшее, b – наибольшее значения величин Х.

2. Математическое ожидание постоянной величины равно этой постоянной: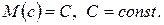

3. Постоянный множитель можно вынести за знак математического ожидания:

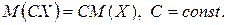
4. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:

.

Это равенство распространяется и на п случайных величин.

5. Математическое ожидание разности двух случайных величин равно разности их математических ожиданий:

.

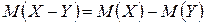6. Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин:

.

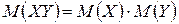Это равенство распространяется и на п независимых случайных величин.

Пример 1.4. Найти математическое ожидание случайной величины 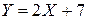, если известно, что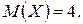

Пример 1.5. Известны математические ожидания двух независимых случайных величин , 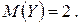Найти математическое ожидание суммы, разности и произведения этих величин.

,

,

.

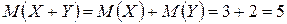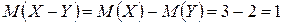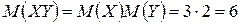На практике, кроме математического ожидания, которое в определенном смысле характеризует центр распределения вероятностей, применяются и другие числовые характеристики, в частности, мода и медиана случайной величины.

Модой непрерывной случайной величины Х называется такое ее значение Х_М, при котором плотность вероятности имеет максимум. Мода дискретной случайной величины определяется как такое возможное значение Х_М, для которого

.

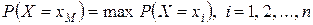Таким образом, мода дискретной случайной величины Х есть ее наиболее вероятное значение, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное распределение) или иметь множество значений (мультимодальное распределение).

Медианой х_me случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего и меньшего значений случайной величины, т. е.

.

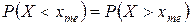Происхождение термина «математическое ожидание» связано с начальным периодом возникновения теории вероятностей (ХVI – ХVII вв.), когда область ее применения ограничивалась азартными играми. Игрока интересовало среднее значение ожидаемого выигрыша, или, иными словами, математическое ожидание выигрыша.

Вопросы для самопроверки

1. Как определяется математическое ожидание дискретной случайной величины, принимающей конечное множество значений?

2. Какие другие названия используются для математического ожидания? Чем объясняются эти названия?

3. Что называют математическим ожиданием дискретной случайной величины, принимающей счетное множество значений?

4. Как определяется математическое ожидание непрерывной случайной величины, все значения которой принадлежат отрезку ?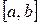

5. Как определяется математическое ожидание непрерывной случайной величины, все значения которой принадлежат бесконечному промежутку ?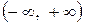

6. Каковы свойства математического ожидания случайной величины?

7. Какому условию должны удовлетворять случайные величины Х и Y, чтобы выполнялось равенство:

?

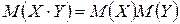8. Докажите, что математическое ожидание неотрицательной дискретной случайной величины неотрицательно.

9. Как определяются мода и медиана случайной величины?